Skip to main content
Chemistry LibreTexts

10.9: Electron Shells

  1. Last updated
  2. Save as PDF
  • Page ID
    477216

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

    ( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\id}{\mathrm{id}}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\kernel}{\mathrm{null}\,}\)

    \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\)

    \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\)

    \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    \( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

    \( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

    \( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vectorC}[1]{\textbf{#1}} \)

    \( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

    \( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

    \( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)
    Learning Objectives
    • Explain the trend of filling energy levels with electrons.
    • Explain the connection between valence electrons and the periodic law.

    From both the Bohr model and quantum mechanics we now know that electrons are arranged in an orderly manner of energy levels. In this final section, we will see how this particular arrangement of electrons relates back to the periodic law.

    Electron Shells

    The energy levels for the electrons in an atom are often referred to as electron shells. (Note: as we discussed previously, this does not refer to movement according to classical mechanics, but an indication of increasing potential energy as the shell number increases.) These shells are given notations 1n, 2n, etc. to indicate the increasing potential energy of each shell, as indicated in Figure \(\PageIndex{1}\) Each of these energy levels contains one or more orbitals that have a limited number of electrons that they may hold. The electrons are generally added to the lowest energy orbital available. When the available orbitals within one energy level have been filled, any additional electrons must be added to the next energy level. In addition to being of a higher potential energy, each successive energy level has a greater number of orbitals it contains, and therefore a greater capacity to contain electrons. As the number of orbitals within an energy level increases, there is a bit more complexity to the order in which the electrons are added. The details of this complexity are beyond the scope of this course, but we will mention some of their implications as it relates to the effects this has on periodic trends.

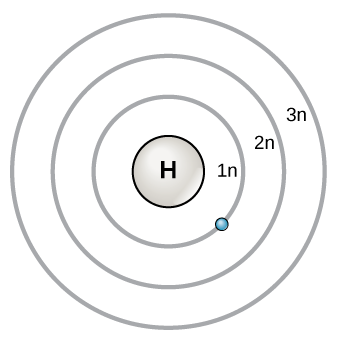
    Three concentric circles around the nucleus of a hydrogen atom represent principal shells. These are named 1n, 2n, and 3n in order of increasing distance from the nucleus. An electron orbits in the shell closest to the nucleus, 1n.
    Figure \(\PageIndex{1}\): The electron shell model is consistent with both the Bohr model and quantum mechanics.

    When we begin to add these electrons to an energy level, we start to see a trend emerge that mirrors the trend first observed by Mendeleev. At some point an electron shell will be filled with electrons. Regardless of which electron shell we are talking about, the significance of a filled electron shell has vast implications for the chemical properties of that atom. If we imagine an atom with one additional electron, we end up with an atom that has a single electron in its outer electron shell. Likewise, the significance of an electron shell with a single electron has vast implications on the chemical properties of that atom. Figure \(\PageIndex{2}\) shows models of these electron shells for a portion of the periodic table. Note that each element in group 1 has a single electron in its outer energy shell, and that each element in group 18 has that energy shell filled (though the number of electrons necessary to fill it changes from 2 to 8 after the first shell). Also note that groups 14 and 17 have identical numbers of electrons in their outer energy level. This trend is so significant that we have a special name for the electrons in the outermost electron shell: valence electrons. It turns out that most of the chemical properties of greatest importance to the function of life occur because of the behavior of these electrons. We shall explore the behavior of these electrons in more detail later in this text.

    Bohr diagrams of elements from groups 1, 14, 17 and 18, and periods 1, 2 and 3 are shown. Period 1, in which the 1n shell is filling, contains hydrogen and helium. Hydrogen, in group 1, has one valence electron. Helium, in group 18, has two valence electrons. The 1n shell holds a maximum of two electrons, so the shell is full and the electron configuration is stable. Period 2, in which the 2n shell is filling, contains lithium, carbon, fluorine, and neon. Lithium, in group 1, has 1 valence electron. Carbon, in group 14, has 4 valence electrons. Fluorine, in group 17, has 7 valence electrons. Neon, in group 18, has 8 valence electrons, a full octet. Period 3, in which the 3n shell is filling, contains sodium, silicon, chlorine, and argon. Sodium, in group 1, has 1 valence electron. Silicon, in group 14, has 4 valence electrons. Chlorine, in group 17, has 7 valence electrons. Argon, in group 18, has 8 valence electrons, a full octet.
    Figure \(\PageIndex{2}\): electron shell models focusing on the valence electrons for select groups of the period table within the first three periods.

    Valence Electrons and the Periodic Law

    It turns out that the reason why the periodic law works as a predictor of chemical properties is because of the behavior of the valence electrons. If we look at a periodic table, such as the one shown in Figure \(\PageIndex{3}\), we can see how some of these trends emerge. The groups which have the greatest similarities in chemical properties were the ones to which we ascribed special names: alkali metals, alkaline earth metals, halogens, and noble gases. Note that these are the positions on the periodic table where the valence electron shell is full, nearly full, or nearly empty. The tendency towards a full valence electron shell is so important that the elements within each of these groups become almost identical in their chemical properties. Elsewhere on the periodic table these trends exist, but are not as pronounced. In fact the areas of the period table we had designated as blocks even though they encompassed several groups (transition metals, lanthanides, actinides) have more complex chemistry because it sometimes involves electrons that are not in the valence shell.

    The periodic table consists of eighteen groups and seven periods. Two additional rows of elements, known as the lanthanides and actinides, are placed beneath the main table. The lanthanides include elements 57 through 71 and belong in period seven between groups three and four. The actinides include elements 89 through 98 and belong in period eight between the same groups. These elements are placed separately to make the table more compact. For each element, the name, atomic symbol, atomic number, and atomic mass are provided. The atomic number is a whole number that represents the number of protons. The atomic mass, which is the average mass of different isotopes, is estimated to two decimal places. For example, hydrogen has the atomic symbol H, the atomic number 1, and an atomic mass of 1.01. The atomic mass is always larger that the atomic number. For most small elements, the atomic mass is approximately double the atomic number as the number of protons and neutrons is about equal. The elements are divided into three categories: metals, nonmetals and metalloids. These form a diagonal line from period two, group thirteen to period seven, group sixteen. All elements to the left of the metalloids are metals, and all elements to the right are nonmetals.
    Figure \(\PageIndex{3}\): The periodic table showing groupings of elements (note: the metalloids have been omitted from this table.)

    Ironically, Mendeleev never actually believed in electrons, even though they were the factor that could explain the natural law he had discovered! This is often an unfortunate trend among established scientists who are not able to recognize the contributions of those who come along after them. Nevertheless the progress of science has continued to move along. However, it is an important life lesson to realize that even as teachers there are things we might learn from our students.

    Section Summary

    • Energy levels are predicted by both the Bohr model and quantum mechanics.
    • Electrons typically fill orbitals of the highest vacant energy level.
    • Electrons in the outermost energy level are called valence electrons.
    • Valence electrons predict chemical properties, and thereby the periodic law.

    Glossary

    electron shells
    the energy levels of the electrons within an atom.
    orbitals
    most precise information typically available about the energy and location of an electron. Capable of containing up to two electrons.
    valence electrons
    electrons found in the outermost electron shell.

    Contributors and Attributions

    CC licensed content, Shared previously

    This page titled 10.9: Electron Shells is shared under a CC BY-NC-SA license and was authored, remixed, and/or curated by Jamie MacArthur.

    1. Back to top
    • Was this article helpful?

    Recommended articles

    1. Article type
      Section or Page
      Author
      Jamie MacArthur
      License
      CC BY-NC-SA
      OER program or Publisher
      Lumen
    2. Tags
      1. source[1]-bio-43537
      2. source[1]-chem-223215