3.10: Rotation

Learning Objectives

• Describe uniform circular motion.
• Know the rotational analogs for translational measures of motion, force, and momentum.

So far we have considered in detail the movement of particles in straight lines: changes in their direction, velocity, acceleration, and momentum, as well as the forces acting on those objects to cause them to move (or in some cases prevent them from moving). This is often referred to as translational motion. But we also know that objects can rotate and move in circular paths. Can the laws of motion address this sort of movement as well? It turns out that they can, but to do so requires a bit more effort. We are not going to develop all of the relationships here, but we will discuss a few of the definitions and principles involved. With these in place we will be able to then discuss some of the implications of this type of movement.

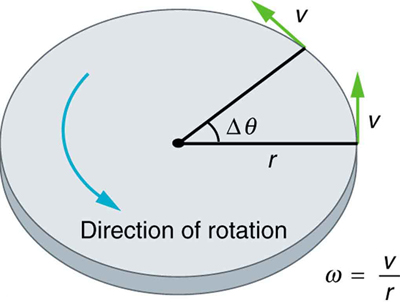
Previously, we looked at uniform circular motion, where an object moves in a circular path at a constant speed (but changing directions, so it undergoes centripetal acceleration). We can also describe this in terms of a rotation at a constant rate. For example, an object completing a circle every second can be said to rotate at a constant rate of 360 degrees per second about the center of the circle (since there are 360 degrees in one complete circle). This type of motion is referred to as angular motion. As we discuss angular motion, we will consider things like angular velocity, angular acceleration, and angular momentum. We will also introduce new analogs for displacement and mass in the concepts of change of angle and moment of inertia.

For the formulas and equations you will see in this section, we will introduce a mathematically convenient unit of angle called radians. An angular measure in radian is defined by the arc length covered by the angle divided by the radius of the circle that the arc length is part of. It turns out that if we do this, we can then define the angular velocity as the speed of the object rotating divided by the radius about which it rotates. This will then affect our definitions of angular acceleration and angular momentum (which are summarized in a table later in this section).

Figure \(\PageIndex{1}\): This figure shows uniform circular motion and some of its defined quantities.

The other thing we must consider for the rotation of objects is that it often becomes more challenging to consider them to be mere particles. As a reminder, a particle is when we consider objects as a point mass where we can ignore the size and shape of the object itself. This is an assumption we make in order to simplify the calculations involved. For many rotating objects this is assumption is no longer valid and we must instead consider how the shape of the object affects the way in which it will rotate. In order to do this we must define a way of keeping track of the inertia of a moving object more complicated than a point mass. The inertia of this object is instead understood to be the summation of all the point masses that make it up modified by the relationship of those objects to the radius around which they are rotating. The result of this calculation is referred to as the moment of inertia, and is often given the symbol I. This value, I, will be the angular motion analog to the m in translational motion. Calculating the moment of inertia is rather complicated, but you can learn more about it in other texts if you are interested.

At this point we can define the remaining rotational measures in terms of analogs of translational dynamics. There are many lower case Greek letters which are often used for these measures. \(\theta\) (theta) is used to indicate a measure of the angle. \(\omega\) (omega) is used to indicate a measure of the angular velocity. \(\alpha\) is used to indicate a measure of the angular acceleration. Force effected to cause turning is referred to as torque, and \(\tau\) (tau) is used to indicate a measure of this torque. These and the remaining rotational analaogs of translational movement are summarized in the following table. For the purpose of this text we are mainly concerned with realizing that each aspect of dynamics we have considered for translation has an analog for rotation.

Rotational and Translational Quantities

Rotational	Translational	Relationship
\(\theta\)	\(x\)	\(\theta=\frac{x}{r}\)
\(\omega\)	\(v\)	\(\omega=\frac{v}{r}\)
\(\alpha\)	\(a\)	\(\alpha=\frac{a_{t}}{r}\)
\(\tau\)	F	\[\tau=mr^{2}\alpha \nonumber\]
\(I\)	m	depends on shape
\(L\)	\(p\)	L=I\(\omega\)

MAKING CONNECTIONS: TAKE-HOME EXPERIMENT

Sit down with your feet on the ground on a chair that rotates. Lift one of your legs such that it is unbent (straightened out). Using the other leg, begin to rotate yourself by pushing on the ground. Stop using your leg to push the ground but allow the chair to rotate. From the origin where you began, sketch the angle, angular velocity, and angular acceleration of your leg as a function of time in the form of three separate graphs. Estimate the magnitudes of these quantities.

Section Summary

• Uniform circular motion is the motion with a constant angular velocity \(\omega=\frac{\Delta \theta}{\Delta t}\).
• In non-uniform circular motion, the velocity changes with time and the rate of change of angular velocity (i.e. angular acceleration) is \(\alpha=\frac{\Delta \omega}{\Delta t}\).
• Linear or tangential acceleration refers to changes in the magnitude of velocity but not its direction, given as \(a_{\mathrm{t}}=\frac{\Delta v}{\Delta t}\).
• Linear or tangential motion variables \(x\), \(v\), and \(a_{t}\) are proportional to the rotational quantities \(\theta\), \(\omega\), and \(\alpha\). They are also proportional to the radius \(r\) of the rotational motion.

Glossary

angular acceleration

the rate of change of angular velocity with time

angular velocity

the rate of change of angular position with time

change in angular velocity

the difference between final and initial values of angular velocity

radian

a unit of angular measure defined by the arc length covered by the angle divided by the radius of the circle that the arc length is part of; one full circle is \(2 \pi\) radians.

Contributors

Curated from resources found in Introduction to Physics published by OpenStax.

tangential acceleration

the acceleration in a direction tangent to the circle at the point of interest in circular motion