4.12: Reading- Budget Constraints and Choices
- Page ID
- 249245
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Budget Constraint Framework
For most of us, the idea of scarcity and trade-offs is something we experience in a very real way when it comes to our own budget constraints. Most of us have a limited amount of money to spend on the things we need and want. Another kind of budget constraint is time. For instance, as a student, you only have twenty-four hours in the day to study, eat, sleep, and check Facebook. An hour spent studying economics is an hour that can’t be used for sleep or play (or something else). As a result, you have to make choices and trade-offs.
In economics, a budget constraint refers to all possible combinations of goods that someone can afford, given the prices of goods, when all income (or time) is spent.
Take the following example of someone who must choose between two different goods: Charlie has $10 in spending money each week that he can allocate between bus tickets for getting to work and the burgers he eats for lunch. Burgers cost $2 each, and bus tickets are 50 cents each. Figure 1, below, shows Charlie’s budget constraint ($10) and all the possible combinations of burgers and bus tickets he can afford if he spends all his money.
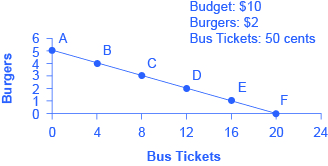
The vertical axis in the figure shows burger purchases, and the horizontal axis shows bus ticket purchases. If Charlie spends all his money on burgers, he can afford five per week. ($10 per week/$2 per burger = 5 burgers per week.) But if he does this, he won’t be able to afford any bus tickets. This choice (zero bus tickets and 5 burgers) is shown by point A in the figure. Alternatively, if Charlie spends all his money on bus tickets, he can afford 20 per week. ($10 per week/$0.50 per bus ticket = 20 bus tickets per week.) Then, however, he will not be able to afford any burgers. This alternative choice (20 bus tickets and zero burgers) is shown by point F. The slope of the budget constraint is determined by the relative price of burgers and bus tickets.
If Charlie is like most people, he will choose some combination that includes both bus tickets and burgers—that is, he will choose one of the points along the budget-constraint line that connects points A and F. Each point inside or on the budget constraint shows a combination of burgers and bus tickets that Charlie can afford. (A point inside the curve is definitely an option—it just means that Charlie isn’t spending all his money.) Keep in mind that the curve represents the maximum number of burgers and bus tickets he can buy. Any point outside the constraint is not affordable, because it would cost more money than Charlie has in his budget.
The budget constraint clearly shows the trade-off Charlie faces in choosing between burgers and bus tickets. Suppose he is currently at point D, where he can afford 12 bus tickets and 2 burgers. What would it cost Charlie for one more burger? It would be natural to answer $2, but that’s not the way economists think. Instead, they ask: How many bus tickets would Charlie have to give up to get one more burger, while staying within his budget? The answer is four bus tickets. That is the true cost to Charlie of one more burger.
A budget-constraint diagram like the one above, with just two goods—burgers and bus tickets—is simple and not very realistic. After all, in an economy like ours (and Charlie’s), people choose from thousands of goods. However, economists use graphs and models to illustrate that every choice has an opportunity cost, which is the point that carries over to the real world.
Sunk Costs
In the budget constraint framework, all decisions involve what will happen next: What quantities of goods will you consume? How many hours will you work? How much will you save? Choices made or costs in the past are not taken into account. The budget constraint framework assumes that sunkcosts—costs incurred in the past that can’t be recovered—should not affect the current decision.
Suppose you pay $8 to see a movie, but after watching the first thirty minutes, you decide that it’s awful. Should you stick it out and watch the rest because you paid for the ticket, or should you leave? The money you spent on the ticket is a sunk cost, and unless the theater manager is feeling generous, you won’t get a refund. But staying for the rest of the movie means paying an opportunity cost in time. Your choice is whether to spend the next ninety minutes suffering through a rotten movie or do something—anything—else. The lesson of sunk costs is to forget about the money and time that is irretrievably gone and to focus, instead, on the costs and benefits of current and future options. A sunk cost is water under the bridge, so to speak.
For people and organizations alike, dealing with sunk costs can be frustrating and difficult. For one thing, it often means admitting an earlier error of judgment. Many companies find it hard to give up on a new product that’s doing poorly because they’ve invested so much time and money in the product development and launch. But the lesson of sunk costs is to ignore them and make decisions based on what will happen in the future.
- Revision and adaptation. Provided by: Lumen Learning. License: CC BY: Attribution
- Principles of Microeconomics Chapter 2.1. Authored by: OpenStax College. Provided by: Rice University. Located at: http://cnx.org/contents/ea2f225e-6063-41ca-bcd8-36482e15ef65@10.31:24/Microeconomics. License: CC BY: Attribution. License Terms: Download for free at http://cnx.org/content/col11627/latest
- Huracan Burger. Authored by: Francisco Schmidt. Located at: https://www.flickr.com/photos/holacomovai/2500903782/. License: CC BY-NC: Attribution-NonCommercial
- The Hermitage Bridge. Authored by: Cat Burton. Located at: https://www.flickr.com/photos/catburton/8416528193/. License: CC BY-NC-ND: Attribution-NonCommercial-NoDerivatives



