4.9: Reaction Yields
- Page ID
- 233010
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Learning Objectives
By the end of this section, you will be able to:
- Explain the concepts of theoretical yield and limiting reactants/reagents.
- Derive the theoretical yield for a reaction under specified conditions.
- Calculate the percent yield for a reaction.
The relative amounts of reactants and products represented in a balanced chemical equation are often referred to as stoichiometric amounts. All the exercises of the preceding module involved stoichiometric amounts of reactants. For example, when calculating the amount of product generated from a given amount of reactant, it was assumed that any other reactants required were available in stoichiometric amounts (or greater). In this module, more realistic situations are considered, in which reactants are not present in stoichiometric amounts.
Limiting Reactant
Consider another food analogy, making grilled cheese sandwiches (Figure 1):
Stoichiometric amounts of sandwich ingredients for this recipe are bread and cheese slices in a 2:1 ratio. Provided with 28 slices of bread and 11 slices of cheese, one may prepare 11 sandwiches per the provided recipe, using all the provided cheese and having six slices of bread left over. In this scenario, the number of sandwiches prepared has been limited by the number of cheese slices, and the bread slices have been provided in excess.

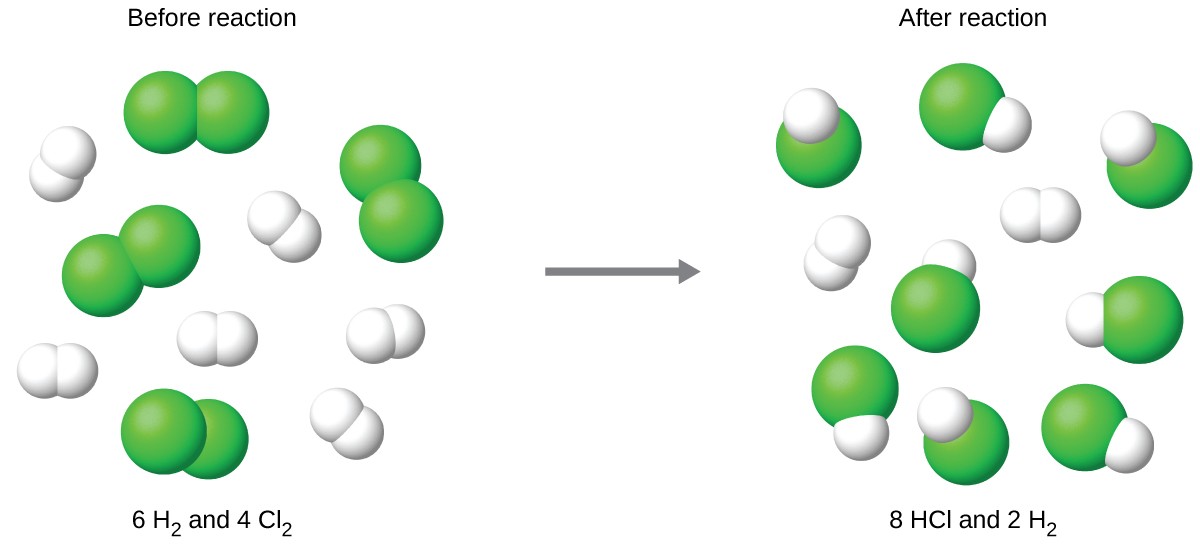
Consider this concept now with regard to a chemical process, the reaction of hydrogen with chlorine to yield hydrogen chloride:
The balanced equation shows the hydrogen and chlorine react in a 1:1 stoichiometric ratio. If these reactants are provided in any other amounts, one of the reactants will nearly always be entirely consumed, thus limiting the amount of product that may be generated. This substance is the limiting reactant, and the other substance is the excess reactant. Identifying the limiting and excess reactants for a given situation requires computing the molar amounts of each reactant provided and comparing them to the stoichiometric amounts represented in the balanced chemical equation. For example, imagine combining 3 moles of H2 and 2 moles of Cl2. This represents a 3:2 (or 1.5:1) ratio of hydrogen to chlorine present for reaction, which is greater than the stoichiometric ratio of 1:1. Hydrogen, therefore, is present in excess, and chlorine is the limiting reactant. Reaction of all the provided chlorine (2 mol) will consume 2 mol of the 3 mol of hydrogen provided, leaving 1 mol of hydrogen unreacted.
An alternative approach to identifying the limiting reactant involves comparing the amount of product expected for the complete reaction of each reactant. Each reactant amount is used to separately calculate the amount of product that would be formed per the reaction’s stoichiometry. The reactant yielding the lesser amount of product is the limiting reactant. For the example in the previous paragraph, complete reaction of the hydrogen would yield
Complete reaction of the provided chlorine would produce
The chlorine will be completely consumed once 4 moles of HCl have been produced. Since enough hydrogen was provided to yield 6 moles of HCl, there will be unreacted hydrogen remaining once this reaction is complete. Chlorine, therefore, is the limiting reactant and hydrogen is the excess reactant (Figure 2).
Example 1: Identifying the Limiting Reactant
Silicon nitride is a very hard, high-temperature-resistant ceramic used as a component of turbine blades in jet engines. It is prepared according to the following equation:
Which is the limiting reactant when 2.00 g of Si and 1.50 g of N2 react?
[reveal-answer q=”839920″]Show Answer[/reveal-answer]
[hidden-answer a=”839920″]
Compute the provided molar amounts of reactants, and then compare these amounts to the balanced equation to identify the limiting reactant.
The provided Si:N2 molar ratio is:
The stoichiometric Si:N2 ratio is:
Comparing these ratios shows that Si is provided in a less-than-stoichiometric amount, and so is the limiting reactant.
Alternatively, compute the amount of product expected for complete reaction of each of the provided reactants. The 0.0712 moles of silicon would yield
while the 0.0535 moles of nitrogen would produce
Since silicon yields the lesser amount of product, it is the limiting reactant.
[/hidden-answer]
Check Your Learning
Which is the limiting reactant when 5.00 g of H2 and 10.0 g of O2 react and form water?
[reveal-answer q=”417358″]Show Answer[/reveal-answer]
[hidden-answer a=”417358″]O2[/hidden-answer]
Percent Yield
The amount of product that may be produced by a reaction under specified conditions, as calculated per the stoichiometry of an appropriate balanced chemical equation, is called the theoretical yield of the reaction. In practice, the amount of product obtained is called the actual yield, and it is often less than the theoretical yield for a number of reasons. Some reactions are inherently inefficient, being accompanied by side reactions that generate other products. Others are, by nature, incomplete (consider the partial reactions of weak acids and bases discussed earlier in this chapter). Some products are difficult to collect without some loss, and so less than perfect recovery will reduce the actual yield. The extent to which a reaction’s theoretical yield is achieved is commonly expressed as its percent yield:
Actual and theoretical yields may be expressed as masses or molar amounts (or any other appropriate property; e.g., volume, if the product is a gas). As long as both yields are expressed using the same units, these units will cancel when percent yield is calculated.
Example 2: Calculation of Percent Yield
Upon reaction of 1.274 g of copper sulfate with excess zinc metal, 0.392 g copper metal was obtained according to the equation:
What is the percent yield?
[reveal-answer q=”115156″]Show Answer[/reveal-answer]
[hidden-answer a=”115156″]
The provided information identifies copper sulfate as the limiting reactant, and so the theoretical yield is found by the approach illustrated in the previous module, as shown here:
Using this theoretical yield and the provided value for actual yield, the percent yield is calculated to be
[/hidden-answer]
Check Your Learning
What is the percent yield of a reaction that produces 12.5 g of the Freon CF2Cl2 from 32.9 g of CCl4 and excess HF?
[reveal-answer q=”829702″]Show Answer[/reveal-answer]
[hidden-answer a=”829702″]48.3%[/hidden-answer]
Green Chemistry and Atom Economy
The purposeful design of chemical products and processes that minimize the use of environmentally hazardous substances and the generation of waste is known as green chemistry. Green chemistry is a philosophical approach that is being applied to many areas of science and technology, and its practice is summarized by guidelines known as the “Twelve Principles of Green Chemistry” (see details at the EPA’s “Green Chemistry” website). One of the 12 principles is aimed specifically at maximizing the efficiency of processes for synthesizing chemical products. The atom economy of a process is a measure of this efficiency, defined as the percentage by mass of the final product of a synthesis relative to the masses of all the reactants used:
Though the definition of atom economy at first glance appears very similar to that for percent yield, be aware that this property represents a difference in the theoretical efficiencies of different chemical processes. The percent yield of a given chemical process, on the other hand, evaluates the efficiency of a process by comparing the yield of product actually obtained to the maximum yield predicted by stoichiometry.
The synthesis of the common nonprescription pain medication, ibuprofen, nicely illustrates the success of a green chemistry approach (Figure 3). First marketed in the early 1960s, ibuprofen was produced using a six-step synthesis that required 514 g of reactants to generate each mole (206 g) of ibuprofen, an atom economy of 40%. In the 1990s, an alternative process was developed by the BHC Company (now BASF Corporation) that requires only three steps and has an atom economy of ~80%, nearly twice that of the original process. The BHC process generates significantly less chemical waste; uses less-hazardous and recyclable materials; and provides significant cost-savings to the manufacturer (and, subsequently, the consumer). In recognition of the positive environmental impact of the BHC process, the company received the Environmental Protection Agency’s Greener Synthetic Pathways Award in 1997.
![This figure is labeled, “a,” and, “b.” Part a shows an open bottle of ibuprofen and a small pile of ibuprofen tablets beside it. Part b shows a reaction along with line structures. The first line structure looks like a diagonal line pointing down and to the right, then up and to the right and then down and to the right. At this point it connects to a hexagon with alternating double bonds. At the first trough there is a line that points straight down. From this structure, there is an arrow pointing downward. The arrow is labeled, “H F,” on the left and “( C H subscript 3 C O ) subscript 2 O,” on the right. The next line structure looks exactly like the first line structure, but it has a line angled down and to the right from the lower right point of the hexagon. This line is connected to another line which points straight down. Where these two lines meet, there is a double bond to an O atom. There is another arrow pointing downward, and it is labeled, “H subscript 2, Raney N i.” The next structure looks very similar to the second, previous structure, except in place of the double bonded O, there is a singly bonded O H group. There is a final reaction arrow pointing downward, and it is labeled, “C O, [ P d ].” The final structure is similar to the third, previous structure except in place of the O H group, there is another line that points down and to the right to an O H group. At these two lines, there is a double bonded O.](https://chem.libretexts.org/@api/deki/files/289938/CNX_Chem_04_04_GreenChem1.jpg?revision=1)
Key Concepts and Summary
When reactions are carried out using less-than-stoichiometric quantities of reactants, the amount of product generated will be determined by the limiting reactant. The amount of product generated by a chemical reaction is its actual yield. This yield is often less than the amount of product predicted by the stoichiometry of the balanced chemical equation representing the reaction (its theoretical yield). The extent to which a reaction generates the theoretical amount of product is expressed as its percent yield.
Key Equations
Exercises
- The following quantities are placed in a container: 1.5 × 1024 atoms of hydrogen, 1.0 mol of sulfur, and 88.0 g of diatomic oxygen.
- What is the total mass in grams for the collection of all three elements?
- What is the total number of moles of atoms for the three elements?
- If the mixture of the three elements formed a compound with molecules that contain two hydrogen atoms, one sulfur atom, and four oxygen atoms, which substance is consumed first?
- How many atoms of each remaining element would remain unreacted in the change described in (c)?
- What is the limiting reactant in a reaction that produces sodium chloride from 8 g of sodium and 8 g of diatomic chlorine?
- Which of the postulates of Dalton’s atomic theory explains why we can calculate a theoretical yield for a chemical reaction?
- A student isolated 25 g of a compound following a procedure that would theoretically yield 81 g. What was his percent yield?
- A sample of 0.53 g of carbon dioxide was obtained by heating 1.31 g of calcium carbonate. What is the percent yield for this reaction?
- Freon-12, CCl2F2, is prepared from CCl4 by reaction with HF. The other product of this reaction is HCl. Outline the steps needed to determine the percent yield of a reaction that produces 12.5 g of CCl2F2 from 32.9 g of CCl4. Freon-12 has been banned and is no longer used as a refrigerant because it catalyzes the decomposition of ozone and has a very long lifetime in the atmosphere. Determine the percent yield.
- Citric acid, C6H8O7, a component of jams, jellies, and fruity soft drinks, is prepared industrially via fermentation of sucrose by the mold Aspergillus niger. The equation representing this reaction is
. What mass of citric acid is produced from exactly 1 metric ton (1.000 × 103 kg) of sucrose if the yield is 92.30%?
- Toluene, C6H5CH3, is oxidized by air under carefully controlled conditions to benzoic acid, C6H5CO2H, which is used to prepare the food preservative sodium benzoate, C6H5CO2Na. What is the percent yield of a reaction that converts 1.000 kg of toluene to 1.21 kg of benzoic acid?
- In a laboratory experiment, the reaction of 3.0 mol of H2 with 2.0 mol of I2 produced 1.0 mol of HI. Determine the theoretical yield in grams and the percent yield for this reaction.
- Outline the steps needed to solve the following problem, then do the calculations. Ether, (C2H5)2O, which was originally used as an anesthetic but has been replaced by safer and more effective medications, is prepared by the reaction of ethanol with sulfuric acid.
What is the percent yield of ether if 1.17 L (d = 0.7134 g/mL) is isolated from the reaction of 1.500 L of C2H5OH (d = 0.7894 g/mL)?
- Outline the steps needed to determine the limiting reactant when 30.0 g of propane, C3H8, is burned with 75.0 g of oxygen.
Determine the limiting reactant.
- Outline the steps needed to determine the limiting reactant when 0.50 g of Cr and 0.75 g of H3PO4 react according to the following chemical equation?
Determine the limiting reactant.
- What is the limiting reactant when 1.50 g of lithium and 1.50 g of nitrogen combine to form lithium nitride, a component of advanced batteries, according to the following unbalanced equation?
- Uranium can be isolated from its ores by dissolving it as UO2(NO3)2, then separating it as solid UO2(C2O4)
3H2O. Addition of 0.4031 g of sodium oxalate, Na2C2O4, to a solution containing 1.481 g of uranyl nitrate, UO2(NO2)2, yields 1.073 g of solid UO2(C2O4)
3H2O.
Determine the limiting reactant and the percent yield of this reaction.
- How many molecules of C2H4Cl2 can be prepared from 15 C2H4 molecules and 8 Cl2 molecules?
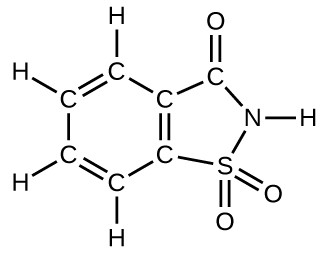
- How many molecules of the sweetener saccharin can be prepared from 30 C atoms, 25 H atoms, 12 O atoms, 8 S atoms, and 14 N atoms?
- The phosphorus pentoxide used to produce phosphoric acid for cola soft drinks is prepared by burning phosphorus in oxygen.
- What is the limiting reactant when 0.200 mol of P4 and 0.200 mol of O2 react according to
- Calculate the percent yield if 10.0 g of P4O10 is isolated from the reaction.
- What is the limiting reactant when 0.200 mol of P4 and 0.200 mol of O2 react according to
- Would you agree to buy 1 trillion (1,000,000,000,000) gold atoms for $5? Explain why or why not. Find the current price of gold at http://money.cnn.com/data/commodities/
[reveal-answer q=”133123″]Show Selected Answers[/reveal-answer]
[hidden-answer a=”133123″]
2. Write the balanced chemical equation and determine the number of moles of each reactant available.
The reaction is:
The stoichiometric ratio is 2 mol Na: 1 mol Cl2; since the reactants are provided in a 0.3:0.1 or 3:1 ratio, Na is present in excess and Cl2 is the limiting reactant.
4.
6. Write and balance the equation for the reaction: Molar masses: CCl4 = 153.82 g/mol; CCl2F2 = 120.89 g/mol. The conversions required are
To find the percent yield, divide the 12.5 g of CCl2F2 by the theoretical mass, and multiply by 100%. For complete conversion,
8.
10. Convert mass of ethanol to moles of ethanol; relate the moles of ethanol to the moles of ether produced using the stoichiometry of the balanced equation. Convert moles of ether to grams; divide the actual grams of ether (determined through the density) by the theoretical mass to determine the percent yield.
Mass ether = 1.184
12. The conversion needed is Then compare the amount of Cr to the amount of acid present.
Thus, 0.25 mol H3PO4 is in excess, so Cr is the limiting reactant.
14. Using the balanced equation, determine which reactant quantity produces the smallest theoretical yield. This quantity represents the largest amount of product that can be produced. Then calculate the percent yield. The conversions for reaction 1 using the nitrate as limiting reactant are.
The answer to this calculation should be compared with the answer from reaction 2 that uses sodium oxalate as the limiting reactant and requires the following conversions:
Molar masses: UO2(NO3)2 = 394.04 g/mol
Na2C2O4 = 134.00 g/mol
UO2(C2O4) 3H2O = 412.09 g/mol
Reaction 1:
Reaction 2:
Based on the two masses, the smaller mass is the limiting reactant. Thus, Na2C2O4 is the limiting reactant. An amount of UO2(NO3)2 is left unreacted.
16. Determine the number of atoms of each element in saccharin and then compare these numbers to the numbers of atoms available. The numbers of atoms in saccharin are seven C atoms, five H atoms, three O atoms, one S atom, and one N atom. Compare these to the numbers of atoms available. Divide each of the required number of atoms into the corresponding number of atoms available. These relationships are 30/7 C, 25/5 H, 12/3 O, 8/1 S, and 14/1 N. The smallest values is four for O, so only four molecules can be made.
18. This amount cannot be weighted by ordinary balances and is worthless.
[/hidden-answer]
Glossary
actual yield: amount of product formed in a reaction
excess reactant: reactant present in an amount greater than required by the reaction stoichiometry
limiting reactant: reactant present in an amount lower than required by the reaction stoichiometry, thus limiting the amount of product generated
percent yield: measure of the efficiency of a reaction, expressed as a percentage of the theoretical yield
theoretical yield: amount of product that may be produced from a given amount of reactant(s) according to the reaction stoichiometry
- Chemistry. Provided by: OpenStax College. Located at: http://openstaxcollege.org. License: CC BY: Attribution. License Terms: Download for free at https://openstaxcollege.org/textbooks/chemistry/get

