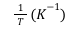2611 Thermodynamics of Borax solubility

Thermodynamics of Borax Solubility

1.0 INTRODUCTION

1.1 Objectives

After completing this experiment, the student will be able to:

• Determine the solubility product constant.
• Generalize the relationship of the solubility product constant and temperature.
• Determine the values of ΔH°, ΔS°, and ΔG° for a reaction.

1.2 Background

In this experiment, you will determine the values of ∆H° and ∆S° for the reaction which occurs when borax (sodium tetraborate octahydrate) dissolves in water.

In previous experiments, you have determined ∆H° values directly, by measuring temperature changes when the reaction occurred. However, in many cases, this technique is not practicable. For example, the reaction may not go to completion, or it may give off such a small amount of heat that the temperature change is too small to measure. In addition, there is no direct method for measuring ∆S° for a reaction. It is therefore useful to be able to determine ∆H° and ∆S° indirectly, by using their relationship to the equilibrium constant of a reaction.

The equilibrium constant of any reaction can be related to the free energy change of the reaction:

∆G° = –RT ln K

The free energy change is also related to the enthalpy and entropy changes during the

reaction:

∆G° = ∆H° – T ∆S°

Combining these two equations gives the general relationship between K, ∆H°, and ∆S°:

–RT ln K = ∆H° – T ∆S°

Dividing both sides by –RT gives a particularly useful form of this relationship:

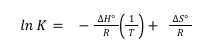
This represents a linear equation of the form y=mx+b. In this case, y=ln K and x= 1/T; a plot of ln K against 1/T will therefore be linear. In addition, the slope of this line (m) will equal –(∆H°/R), and its y-intercept (b) will equal (∆S°/R). It is therefore possible to determine ∆H° and ∆S° by simply measuring the equilibrium constant at two different temperatures, graphing ln K against 1/T, and measuring the slope and intercept of the resulting line. In practice, K is measured at several temperatures, so that the effect of any experimental errors in one measurement will be minimized.

The reaction you will study is the dissolution of borax (sodium tetraborate octahydrate) in water. “Borax” is a naturally occurring compound; it is in fact the most important source of the element boron. Borax has been used for many years as a water softening agent. Borax is a rather complicated ionic salt which has the chemical formula Na2B4O5(OH)4⋅8 H2O. When it dissolves, it dissociates as follows:

Na2B4O5(OH)4.8 H2O (s) ⇌ 2 Na+ (aq) + B4O5(OH)42– (aq) + 8 H2O (l) (1)

Notice that the products of this reaction are two sodium ions and one other ion (this ion is called “tetraborate”), along with the eight molecules of water. Since water does not appear in equilibrium constant expressions, the K expression for this reaction is:

K = [Na+]2[B4O5(OH)42–]

You will measure K by analyzing a saturated solution of borax (i.e. a solution in which Reaction (1) has come to equilibrium!) for the tetraborate ion. Tetraborate is a weak base, so it can be titrated with a strong acid. It may surprise you that tetraborate can react with only two hydrogen ions -- not four! -- and that in this reaction, the tetraborate ion “falls apart”, producing four molecules of boric acid:

B4O5(OH)42– (aq) + 2 H3O+ (aq) + H2O (l) → 4 H3BO3 (aq) (2)

Once you know the number of moles of tetraborate in the solution, you can calculate the number of moles of sodium ion by using the stoichiometry of Reaction (1). Then, you can calculate the molar concentrations of the two ions and, finally, the value of K.

References and further reading

Technique G: Buret Use

Experiment 2501 Using Excel for Graphical Analysis of Data of the laboratory manual

2.0 SAFETY PRECAUTIONS AND WASTE DISPOSAL

3.0 CHEMICALS AND SolutionS

Chemical	Concentration	Approximate Amount	Notes
Borax, Na2B4O5(OH)4	Use as is	25 – 30 g
Hydrochloric acid, HCl	0.5 M	150 mL	Standardized solution, refer to reagent bottle for exact concentration
Bromocresol green		drops	Visually impaired students might also use Congo red is an alternative

4.0 GLASSWARE AND APPARATUS

250 mL beaker (2)	Large beaker for water bath
150 mL beaker	125/250 mL Erlenmeyer flask (4)
10 mL graduate cylinder	50 mL buret
Glass stir rod	Buret clamp
Thermometer	Hot plate
Ring stand	Beaker tongs

Note on Cleaning Glassware: Do not use soap to wash glassware for this experiment or you will be titrating the soap residue as well as the borax (soap is also a base). You should rinse all glassware several times with deionized water before beginning this experiment.

5.0 PROCEDURE

1. PREPARATION OF SATURATED BORAX SAMPLES

It is important that the borax solution be saturated in order to achieve equilibrium between the solid and dissolved phases. If you can see solid borax crystals at the bottom of the beaker you are at equilibrium; if not you should add some additional solid borax until you can see white crystals at the bottom of the solution.

1. Obtain a sample of solid borax. You will need enough borax to reach the 40 mL line in a small beaker (50 or 100-mL). Pour the borax into a 150–mL beaker and add around 80 mL of deionized water.

2. Using your glass stirring-rod, stir the borax solution you have made and place it into an ice-water bath. Insert your thermometer into the solution. Continue to stir the solution gently as it cools. Allow the solution to cool to about 10°C.

3. While your solution is cooling,

1. Label a 250-mL beaker “hot water rinse.” Fill the beaker about half full of deionized water and heat on a hot plate. Keep the temperature of this water between about 60°C to 80°C. You will need this hot deionized water throughout the experiment. Add more deionized water to this beaker as needed.
2. Label four Erlenmeyer flasks “10°C,” “30°C,” “50°C,” and “70°C.”

4. When the saturated borax solution in the 150-mL beaker reaches about 10°C, stop stirring the solution and allow the borax crystals in the solution to settle. This takes about 2 minutes. After the solid has settled measure the temperature in the flask to ±0.1 °C and record this temperature on your data sheet.

5. Pour between 7 and 9 mL of the solution into a 10 mL graduated cylinder. Try to avoid pouring any solid. Read and record the volume of solution you poured into the graduated cylinder to ±0.01 mL. Then pour the solution into the Erlenmeyer flask labeled “10°C.”

6. Using your beaker tongs to grasp the hot water rinse beaker, fill the graduated cylinder with hot deionized water to dissolve any borax crystals that formed on the inside the graduated cylinder and pour this into the Erlenmeyer flask labeled “10°C.” Repeat this rinse once more to be certain that all the borax from the graduated cylinder has been transferred to the Erlenmeyer flask.

7. Bring the volume of water in the Erlenmeyer flasks up to about the 50-mL mark by adding room temperature deionized water. This amount does not need to be exact because adding more or less deionized water will not change the number of borax molecules in the flask.

8. Prepare a second hot-water bath. This will not be used for a rinse, so you may use tap water to fill this second bath. Place the 150-mL beaker containing the borax solution into this hot-water. You may need to clamp the 150-mL beaker in place to keep it from turning over in the bath. Allow the borax solution in the 150-mL beaker to warm to about 30°C while stirring. (Do not use the hot deionized water bath for this or you may contaminate the deionized rinse water with borax from the outside of the 150- mL beaker). Be certain there are still visible crystals at the bottom of the 150-mL beaker so that you know the borax solution is in equilibrium with the solid phase and thus still saturated. If necessary, add more solid borax to the solution so that white crystals are visible at the bottom of the beaker at all times.

9. Be careful not to overheat the borax solution. If you allow the borax to heat past the desired temperature and then cool back down, you may get supersaturation of the borax. This could result in significant errors in your experimental results. Should you overheat the solution, either collect your data at higher temperatures, or discard the borax solution in the proper waste container and prepare a fresh one, being careful not to exceed the temperature desired the second time. (The later trials for this experiment do not need to be at exactly 30°C, 50°C, and 70°C, so long as they are somewhere around these values).

10. When the saturated borax solution reaches about 30°C, stop stirring the solution and allow the borax crystals in the solution to settle as before. Then record the exact temperature of the solution to ±0.1 °C on your data sheet.

11. Using the 10-mL graduated cylinder, transfer 7 to 9 mL of the approximately 30°C borax solution to the 30°C Erlenmeyer flasks recording the actual volume to ±0.01 mL on your data table. Once again make sure no solid borax from the bottom of the 150-mL beaker is transferred to graduated cylinder during this process. Rinse the graduated cylinder twice with the hot deionized rinse water and bring the volume of water in the Erlenmeyer flasks up to about the 50-mL mark by adding room temperature deionized water as before.

12. Using the hot water bath, heat the borax solution to about 50°C and then to 70°C, collecting 7 to 9 mL samples at each temperature and rinsing the graduated cylinder with the hot deionized rinse as before.

13. You may need to add additional borax to the solution in the 150-mL beaker as you heat it to maintain equilibrium. Be certain that for each trial you can see crystals of solid borax at the bottom of the solution in the 150-mL beaker. Also be sure to allow the solution to settle for at least 2 minutes before collecting your 5 samples. Again, be careful not to overheat the borax solution between trials.

5.2 TITRATING SATURATED BORAX SAMPLES

1. Rinse a 250-mL beaker labeled “standardized HCl” with deionized water and then rinse with about 5-mL of the 0.5 M standardized HCl solution. Fill this beaker with about 150 mL of the standardized HCl solution. Record the exact concentration of the standardized 0.5 M HCl solution (as given on the reagent label) on your data sheet. You will use this as your standardized HCl solution throughout the titrations. Should you require additional standardized HCl solution, be sure to check that the concentration is the same as the one on your beaker. If it is different you will need to rinse and refill your buret with this new solution and repeat any titrations underway making note of the new concentration for your calculations.

2. Rinse a 50-mL buret with deionized water and then using about 5-mL of the 0.5 M standardized HCl solution. Fill the buret with standardized HCl. Be certain that there are no small air bubbles in the buret tips and that the tips are pressed in firmly and do not leak. Clamp the buret to a buret clamp on a ring stand, making sure that it is vertical.

3. Add four drops of bromocresol green indicator to each of the Erlenmeyer flasks. The solutions in each should turn a light blue color.

4. Titrate the samples with the standardized HCl solution. Record the initial and final buret reading to ±0.01 mL. Bromocresol green is blue in basic solutions and yellow in acidic solutions, so the color of the endpoint should be green.

6.0 DATA RECORDING SHEET

Last Name

First Name

Partner Name(s)

Date

Molarity of standardized 0.5 M HCl solution: _____________________

Table 1. Titration Data

Approximate temperature	10°C	30°C	50°C	70°C
Measured temperature (to ±0.1 °C)
Volume of B4O5(OH)42– sample (to ±0.01 mL)
Initial Buret Volume (to ±0.01 mL)
Final Buret Volume (to ±0.01 mL)
Volume of HCl added (Final-Initial volumes)
Mole of HCl added
Mole of B4O5(OH)42− titrated
Molarity B4O5(OH)42−
Molarity Na+

* remember to use stoichiometry from the equations in the introduction to calculate moles in the table!

Show a sample calculation below for each of the calculated entries in your table. Remember to consider the stoichiometry of the acid-base titration reaction in your calculations; it is not 1:1.

7.0 CALCULATIONS

1. Use the borate ion concentration to determine Ksp and ln K at each temperature. Convert Celsius temperatures to inverse Kelvin temperatures (1/T). Show a sample calculation below for each of the calculated entries in your table.

Table 2. Data Analysis

Trial	[B4O5(OH)42–]	[Na+]	Ksp	ln K	Measured T (K)
10°C
30°C
50°C
70°C

2. Complete the data analysis table by collecting data from other students.

3. Use Excel to create a graph of ln K versus 1/T for your data. Your graph should have an appropriate title and labeled axes with an appropriate scale. Using the Excel trendline function, add a best-fit line to your plotted data and have Excel display the equation of this line and its R2 value on your graph. Submit the graph with your lab and provide the equation here.

y = ________________________________________________________________

4. Use this graph to determine the values of ∆H^°_rxn and ∆S^°_rxn for the dissolution of borax (chemical equation 1). Be certain to include the proper units for each! Show your calculations. (Check the introduction for help with calculations!)

5. Use the values of ∆H^°_rxn and ∆S^°_rxn you obtained to determine the value of ∆G^°_rxn at 298K for the dissolution of borax. Show your calculations.

6. The literature values for enthalpy and entropy of the dissolution of borax in water are 110 kJ/mol and 380 J/mol-K, respectively. Determine the percent error in your experimentally determined values.

8.0 POST-LAB QUESTIONS

1. Does the solubility of borax increase or decrease with increasing temperature? Use both your physical observations and your Ksp measurements to justify your response.

2. Does your value of ∆Hrxn° suggest that the reaction for the dissolution of borax is exothermic or endothermic? Explain why this result is consistent with your answer to Question 1 above.

3. The value of ∆G^°_rxn that you determined for the dissolution of borax at 25°C should be positive (if not you should check your work). Given that ∆G^°_rxn > 0, how do you explain that some of the borax actually dissolved at 25°C?

4. A geologist removes a sample of water from a lake in Nevada where the water level has been slowly dropping over time. The sample is found to be 0.02 M in borax. The lake is circular in shape and is currently 500 meters in diameter and 50 meters deep. Use your experimental data to predict the level of the lake when borax will begin to precipitate on the shore if the mean temperature of the lake water is 15°C. Assume that the lake is equally deep at all points. (helpful formulas: circumference of a circle = 2πr, volume of a cylinder = 2πrh)