Learning Objectives
- Explain what spectra are.
- Learn the quantum numbers that are assigned to electrons.
There are two fundamental ways of generating light: either heat an object up so hot it glows or pass an electrical current through a sample of matter (usually a gas). Incandescent lights and fluorescent lights generate light via these two methods, respectively.
A hot object gives off a continuum of light. We notice this when the visible portion of the electromagnetic spectrum is passed through a prism: the prism separates light into its constituent colors, and all colors are present in a continuous rainbow (part (a) in Figure \(\PageIndex{1}\) - Prisms and Light). This image is known as a continuous spectrum. However, when electricity is passed through a gas and light is emitted and this light is passed though a prism, we see only certain lines of light in the image (part (b) in Figure \(\PageIndex{1}\) - Prisms and Light). This image is called a line spectrum. It turns out that every element has its own unique, characteristic line spectrum.

Figure \(\PageIndex{1}\): Prisms and Light. (a) A glowing object gives off a full rainbow of colors, which are noticed only when light is passed through a prism to make a continuous spectrum. (b) However, when electricity is passed through a gas, only certain colors of light are emitted. Here are the colors of light in the line spectrum of Hg.
Why does the light emitted from an electrically excited gas have only certain colors, while light given off by hot objects has a continuous spectrum? For a long time, it was not well explained. Particularly simple was the spectrum of hydrogen gas, which could be described easily by an equation; no other element has a spectrum that is so predictable (Figure \(\PageIndex{2}\) - Hydrogen Spectrum).

Figure \(\PageIndex{2}\): Hydrogen Spectrum. The spectrum of hydrogen was particularly simple and could be predicted by a simple mathematical expression.
In 1913, the Danish scientist Niels Bohr suggested a reason why the hydrogen atom spectrum looked this way. He suggested that the electron in a hydrogen atom could not have any random energy, having only certain fixed values of energy that were indexed by the number n (the quantum number). Quantities that have certain specific values are quantized values. Bohr suggested that the energy of the electron in hydrogen was quantized because it was in a specific orbit. Because the energies of the electron can have only certain values, the changes in energies can have only certain values (somewhat similar to a staircase: not only are the stair steps set at specific heights but the height between steps is fixed). Finally, Bohr suggested that the energy of light emitted from electrified hydrogen gas was equal to the energy difference of the electron’s energy states:
\[E_{light}=h\nu =\frac{hc}{\lambda}=\Delta E_{electron}\]
This means that only certain frequencies - (and thus, certain wavelengths (\lambda)) of light are emitted. Figure \(\PageIndex{3}\) - Bohr’s Model of the Hydrogen Atom, shows a model of the hydrogen atom based on Bohr’s ideas.
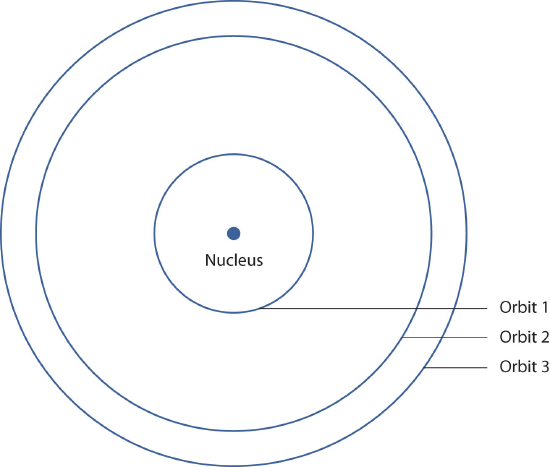
Figure \(\PageIndex{3}\): Bohr’s Model of the Hydrogen Atom. Bohr’s description of the hydrogen atom had specific orbits for the electron, which had quantized energies.
Bohr’s ideas were useful but were applied only to the hydrogen atom. However, later researchers generalized Bohr’s ideas into a new theory called quantum mechanics, which explains the behavior of electrons as if they were acting as a wave, not as particles. Quantum mechanics predicts two major things: quantized energies for electrons of all atoms (not just hydrogen) and an organization of electrons within atoms. Electrons are no longer thought of as being randomly distributed around a nucleus or restricted to certain orbits (in that regard, Bohr was wrong). Instead, electrons are collected into groups and subgroups that explain much about the chemical behavior of the atom.
In the quantum-mechanical model of an atom, the state of an electron is described by four quantum numbers, not just the one predicted by Bohr. The first quantum number is called the principal quantum number(n). The principal quantum number largely determines the energy of an electron. Electrons in the same atom that have the same principal quantum number are said to occupy an electron shell of the atom. The principal quantum number can be any nonzero positive integer: 1, 2, 3, 4,….
Within a shell, there may be multiple possible values of the next quantum number, the angular momentum quantum number(ℓ). The ℓ quantum number has a minor effect on the energy of the electron but also affects the spatial distribution of the electron in three-dimensional space—that is, the shape of an electron’s distribution in space. The value of the ℓ quantum number can be any integer between 0 and n − 1: ℓ = 0, 1, 2,…, n − 1
Thus, for a given value of n, there are different possible values of ℓ:
| If n equals |
ℓ can be |
| 1 |
0 |
| 2 |
0 or 1 |
| 3 |
0, 1, or 2 |
| 4 |
0, 1, 2, or 3 |
and so forth. Electrons within a shell that have the same value of ℓ are said to occupy a subshell in the atom. Commonly, instead of referring to the numerical value of ℓ, a letter represents the value of ℓ (to help distinguish it from the principal quantum number):
The next quantum number is called the magnetic quantum number (mℓ). For any value of ℓ, there are 2ℓ + 1 possible values of mℓ, ranging from −ℓ to ℓ:
\[−ℓ \lt m_ℓ \lt ℓ\]
or
\[|m_ℓ|\lt ℓ\]
The following explicitly lists the possible values of mℓ for the possible values of ℓ:
The particular value of mℓ dictates the orientation of an electron’s distribution in space. When ℓ is zero, mℓ can be only zero, so there is only one possible orientation. When ℓ is 1, there are three possible orientations for an electron’s distribution. When ℓ is 2, there are five possible orientations of electron distribution. This goes on and on for other values of ℓ, but we need not consider any higher values of ℓ here. Each value of mℓ designates a certain orbital. Thus, there is only one orbital when ℓ is zero, three orbitals when ℓ is 1, five orbitals when ℓ is 2, and so forth. The mℓ quantum number has no effect on the energy of an electron unless the electrons are subjected to a magnetic field—hence its name.
The ℓ quantum number dictates the general shape of electron distribution in space (Figure \(\PageIndex{4}\) - Electron Orbitals). Any s orbital is spherically symmetric (Figure \(\PageIndex{4a}\) - Electron Orbitals, and there is only one orbital in any s subshell. Any p orbital has a two-lobed, dumbbell-like shape (Figure \(\PageIndex{4b}\) - Electron Orbitals); because there are three of them, we normally represent them as pointing along the x-, y-, and z-axes of Cartesian space. The d orbitals are four-lobed rosettes (Figure \(\PageIndex{4c}\) - Electron Orbitals they are oriented differently in space (the one labeled dz2 has two lobes and a torus instead of four lobes, but it is equivalent to the other orbitals). When there is more than one possible value of mℓ, each orbital is labeled with one of the possible values. It should be noted that the diagrams in Figure \(\PageIndex{4}\) are estimates of the electron distribution in space, not surfaces electrons are fixed on.
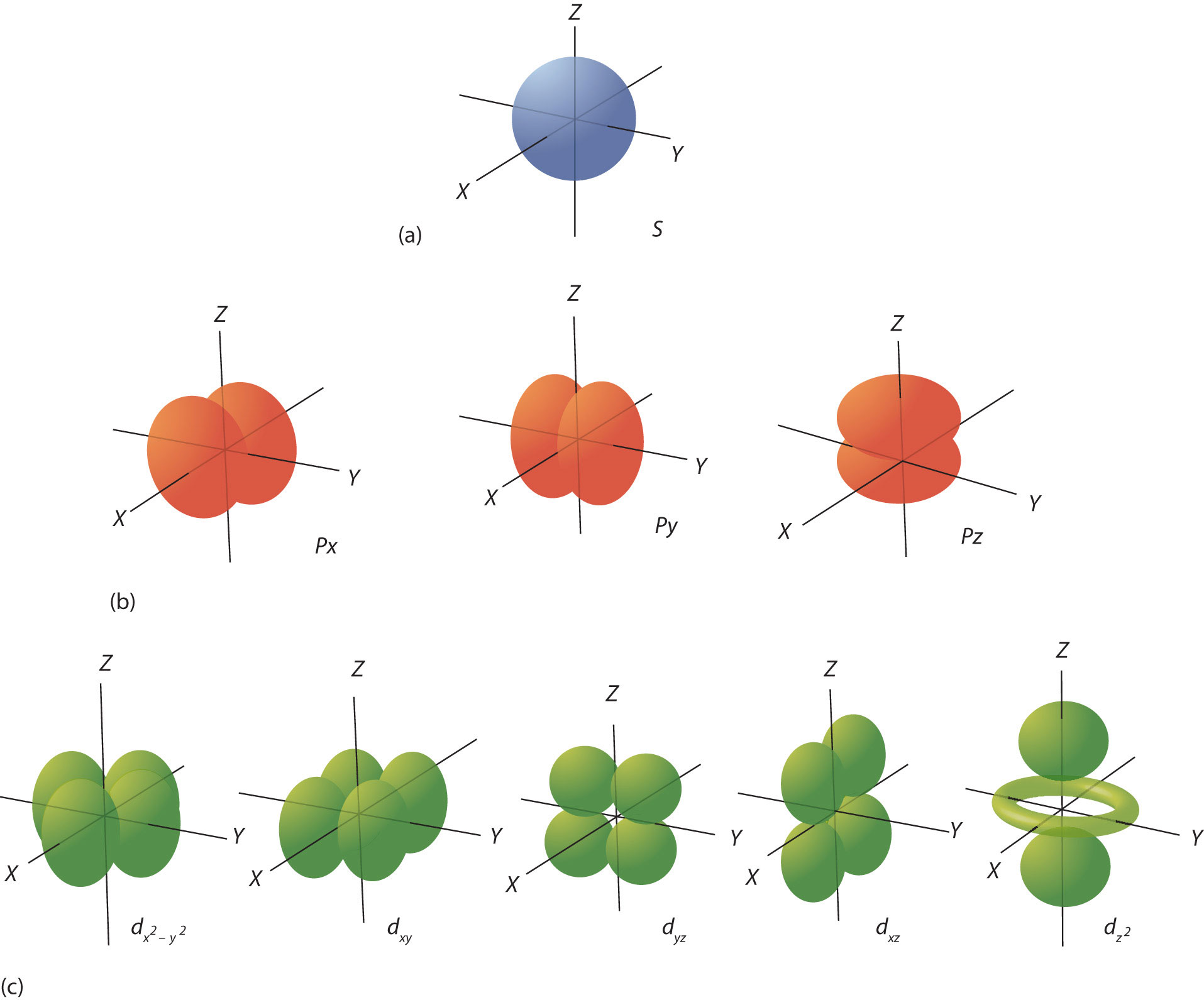
Figure \(\PageIndex{4}\): Electron Orbitals. (a) The lone s orbital is spherical in distribution. (b) The three p orbitals are shaped like dumbbells, and each one points in a different direction. (c) The five d orbitals are rosette in shape, except for the orbital, which is a “dumbbell + torus” combination. They are all oriented in different directions.
The final quantum number is the spin quantum number (ms). Electrons and other subatomic particles behave as if they are spinning (we cannot tell if they really are, but they behave as if they are). Electrons themselves have two possible spin states, and because of mathematics, they are assigned the quantum numbers +1/2 and −1/2. These are the only two possible choices for the spin quantum number of an electron.
Example \(\PageIndex{1}\):
Of the set of quantum numbers {n, ℓ, mℓ, ms}, which are possible and which are not allowed?
- {3, 2, 1, +1/2}
- {2, 2, 0, −1/2}
- {3, −1, 0, +1/2}
Solution
- The principal quantum number n must be an integer, which it is here. The quantum number ℓ must be less than n, which it is. The mℓ quantum number must be between −ℓ and ℓ, which it is. The spin quantum number is +1/2, which is allowed. Because this set of quantum numbers follows all restrictions, it is possible.
- The quantum number n is an integer, but the quantum number ℓ must be less than n, which it is not. Thus, this is not an allowed set of quantum numbers.
- The principal quantum number n is an integer, but ℓ is not allowed to be negative. Therefore this is not an allowed set of quantum numbers.
Exercise \(\PageIndex{1}\)
Of the set of quantum numbers {n, ℓ, mℓ, ms}, which are possible and which are not allowed?
- {4, 2, −2, 1}
- {3, 1, 0, −1/2}
Answers
- Spin must be either +1/2 or −1/2, so this set of quantum number is not allowed.
- allowed
Chemistry Is Everywhere: Neon Lights
A neon light is basically an electrified tube with a small amount of gas in it. Electricity excites electrons in the gas atoms, which then give off light as the electrons go back into a lower energy state. However, many so-called “neon” lights don’t contain neon!
Although we know now that a gas discharge gives off only certain colors of light, without a prism or other component to separate the individual light colors, we see a composite of all the colors emitted. It is not unusual for a certain color to predominate. True neon lights, with neon gas in them, have a reddish-orange light due to the large amount of red-, orange-, and yellow-colored light emitted. However, if you use krypton instead of neon, you get a whitish light, while using argon yields a blue-purple light. A light filled with nitrogen gas glows purple, as does a helium lamp. Other gases—and mixtures of gases—emit other colors of light. Ironically, despite its importance in the development of modern electronic theory, hydrogen lamps emit little visible light and are rarely used for illumination purposes.

Neon lights. The different colors of these “neon” lights are caused by gases other than neon in the discharge tubes. Human/Need/Desire. Neon sculpture by Bruce Nauman (1983), who has been characterized as a conceptual artist. Image used with permission (CC BY-SA 3.0; eschipul).
Key Takeaways
Electrons in atoms have quantized energies. The state of electrons in atoms is described by four quantum numbers.






