8.05: Empirical Formulas

Determination of Empirical Formulas

As previously mentioned, the most common approach to determining a compound’s chemical formula is to first measure the masses of its constituent elements. However, we must keep in mind that chemical formulas represent the relative numbers, not masses, of atoms in the substance. Therefore, any experimentally derived data involving mass must be used to derive the corresponding numbers of atoms in the compound. To accomplish this, we can use molar masses to convert the mass of each element to a number of moles. We then consider the moles of each element relative to each other, converting these numbers into a whole-number ratio that can be used to derive the empirical formula of the substance. Consider a sample of compound determined to contain 1.71 g C and 0.287 g H. The corresponding numbers of atoms (in moles) are:

\[\mathrm{1.17\:g\: C\times \dfrac{1\:mol\: C}{12.01\:g\: C}=0.142\:mol\: C}\]

\[\mathrm{0.287\:g\: H\times \dfrac{1\:mol\: H}{1.008\:g\: H}=0.284\:mol\: H}\]

Thus, we can accurately represent this compound with the formula C_0.142H_0.248. Of course, per accepted convention, formulas contain whole-number subscripts, which can be achieved by dividing each subscript by the smaller subscript:

\[\ce C_{\Large{\frac{0.142}{0.142}}}\:\ce H_{\Large{\frac{0.248}{0.142}}}\ce{\:or\:CH2}\]

(Recall that subscripts of “1” are not written, but rather assumed if no other number is present.)

The empirical formula for this compound is thus CH₂. This may or not be the compound’s molecular formula as well; however, we would need additional information to make that determination (as discussed later in this section).

Consider as another example a sample of compound determined to contain 5.31 g Cl and 8.40 g O. Following the same approach yields a tentative empirical formula of:

\[\mathrm{Cl_{0.150}O_{0.525}=Cl_{\Large{\frac{0.150}{0.150}}}\: O_{\Large{\frac{0.525}{0.150}}}=ClO_{3.5}}\]

In this case, dividing by the smallest subscript still leaves us with a decimal subscript in the empirical formula. To convert this into a whole number, we must multiply each of the subscripts by two, retaining the same atom ratio and yielding Cl₂O₇ as the final empirical formula.

In summary, empirical formulas are derived from experimentally measured element masses by:

1. Deriving the number of moles of each element from its mass
2. Dividing each element’s molar amount by the smallest molar amount to yield subscripts for a tentative empirical formula
3. Multiplying all coefficients by an integer, if necessary, to ensure that the smallest whole-number ratio of subscripts is obtained

Figure \(\PageIndex{1}\) outlines this procedure in flow chart fashion for a substance containing elements A and X.

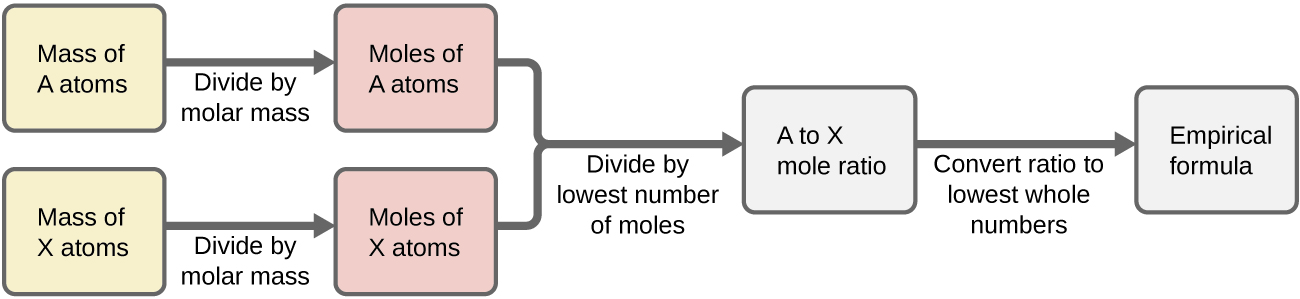
Figure \(\PageIndex{1}\): The empirical formula of a compound can be derived from the masses of all elements in the sample.

Example \(\PageIndex{3}\): Determining an Empirical Formula from Masses of Elements

A sample of the black mineral hematite (Figure \(\PageIndex{2}\)), an oxide of iron found in many iron ores, contains 34.97 g of iron and 15.03 g of oxygen. What is the empirical formula of hematite?

Figure \(\PageIndex{2}\): Hematite is an iron oxide that is used in jewelry. (credit: Mauro Cateb)

Solution

For this problem, we are given the mass in grams of each element. Begin by finding the moles of each:

\[\begin{align}
\mathrm{34.97\:g\: Fe\left(\dfrac{mol\: Fe}{55.85\:g}\right)}&=\mathrm{0.6261\:mol\: Fe}\nonumber\\ \nonumber\\
\mathrm{15.03\:g\: O\left(\dfrac{mol\: O}{16.00\:g}\right)}&=\mathrm{0.9394\:mol\: O} \nonumber
\end{align}\]

Next, derive the iron-to-oxygen molar ratio by dividing by the lesser number of moles:

\[\mathrm{\dfrac{0.6261}{0.6261}=1.000\:mol\: Fe} \nonumber\]

\[\mathrm{\dfrac{0.9394}{0.6261}=1.500\:mol\: O} \nonumber\]

The ratio is 1.000 mol of iron to 1.500 mol of oxygen (Fe₁O_1.5). Finally, multiply the ratio by two to get the smallest possible whole number subscripts while still maintaining the correct iron-to-oxygen ratio:

\[\mathrm{2(Fe_1O_{1.5})=Fe_2O_3}\nonumber\]

The empirical formula is \(Fe_2O_3\).

Exercise \(\PageIndex{3}\)

What is the empirical formula of a compound if a sample contains 0.130 g of nitrogen and 0.370 g of oxygen?

Answer:

\(N_2O_5\)

Video \(\PageIndex{1}\): Additional worked examples illustrating the derivation of empirical formulas are presented in the brief video clip.

Deriving Empirical Formulas from Percent Composition

Finally, with regard to deriving empirical formulas, consider instances in which a compound’s percent composition is available rather than the absolute masses of the compound’s constituent elements. In such cases, the percent composition can be used to calculate the masses of elements present in any convenient mass of compound; these masses can then be used to derive the empirical formula in the usual fashion.

Example \(\PageIndex{4}\): Determining an Empirical Formula from Percent Composition

The bacterial fermentation of grain to produce ethanol forms a gas with a percent composition of 27.29% C and 72.71% O (Figure \(\PageIndex{3}\)). What is the empirical formula for this gas?

Figure \(\PageIndex{3}\): An oxide of carbon is removed from these fermentation tanks through the large copper pipes at the top. (credit: “Dual Freq”/Wikimedia Commons)

Solution Since the scale for percentages is 100, it is most convenient to calculate the mass of elements present in a sample weighing 100 g. The calculation is “most convenient” because, per the definition for percent composition, the mass of a given element in grams is numerically equivalent to the element’s mass percentage. This numerical equivalence results from the definition of the “percentage” unit, whose name is derived from the Latin phrase per centum meaning “by the hundred.” Considering this definition, the mass percentages provided may be more conveniently expressed as fractions:

\[\begin{align}
27.29\,\%\,\ce C&=\mathrm{\dfrac{27.29\:g\: C}{100\:g\: compound}}\nonumber \\ \nonumber \\
72.71\,\%\,\ce O&=\mathrm{\dfrac{72.71\:g\: O}{100\:g\: compound}} \nonumber
\end{align}\]

The molar amounts of carbon and hydrogen in a 100-g sample are calculated by dividing each element’s mass by its molar mass:

\[\begin{align}
\mathrm{27.29\:g\: C\left(\dfrac{mol\: C}{12.01\:g}\right)}&=\mathrm{2.272\:mol\: C} \nonumber \\ \nonumber \\
\mathrm{72.71\:g\: O\left(\dfrac{mol\: O}{16.00\:g}\right)}&=\mathrm{4.544\:mol\: O} \nonumber
\end{align}\]

Coefficients for the tentative empirical formula are derived by dividing each molar amount by the lesser of the two:

\[\mathrm{\dfrac{2.272\:mol\: C}{2.272}=1} \nonumber\]

\[\mathrm{\dfrac{4.544\:mol\: O}{2.272}=2} \nonumber\]

Since the resulting ratio is one carbon to two oxygen atoms, the empirical formula is CO₂.

Exercise \(\PageIndex{4}\)

What is the empirical formula of a compound containing 40.0% C, 6.71% H, and 53.28% O?

Answer:

\(CH_2O\)

Summary

The percent composition of a compound is often experimentally determined and used to derive the compound’s empirical formula. The empirical formula is the lowest whole number ratio of elements in a compound. As multiple compounds can have the same lowest whole number ratio of elements - for example CH₂ is the empirical formula for both C₂H₄ and C₄H₈ - the empirical formula for a compound is not necessarily the same as the compounds molecular formula. 

 

Contributors

• Paul Flowers (University of North Carolina - Pembroke), Klaus Theopold (University of Delaware) and Richard Langley (Stephen F. Austin State University) with contributing authors. Textbook content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at http://cnx.org/contents/85abf193-2bd...a7ac8df6@9.110).