1.3: Bohr's Atom
- Page ID
- 294066
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Review Necessary Skills
- Relate the wavelength (λ) and frequency (ν) of light to the velocity of light (c) (c = λν) and to the energy of a photon (E) (E = hν = hc/λ).
-
Relate charge, distance, and electrostatic potential energy using Coulomb’s law (U = k q1 x q2/r) qualitatively.
-
Describe what happens to molecules when they interact with electromagnetic radiation.
-
What happens to molecules at different wavelengths? See NO2 in this simulation. Don't worry if this doesn't look familiar, it is just a reminder that IR, microwave, and UV light all interact with molecules differently.
-
Experiments that can't be explained without quantization of energy or position
|
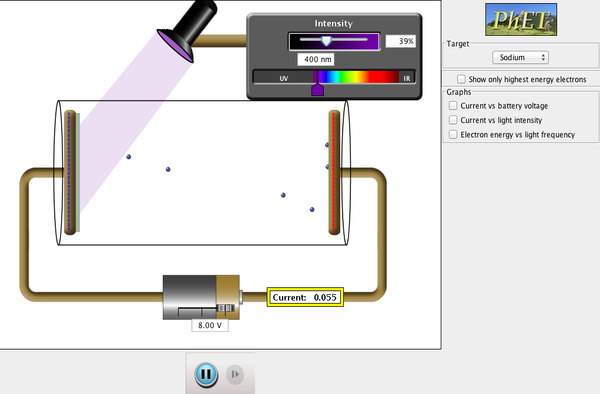
Photoelectric effect (see demo below or go to PheT) |
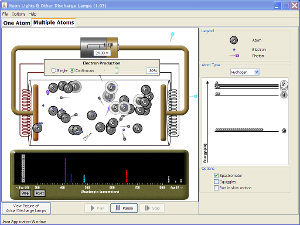
Atomic line spectra (see demo below or go to PheT) |
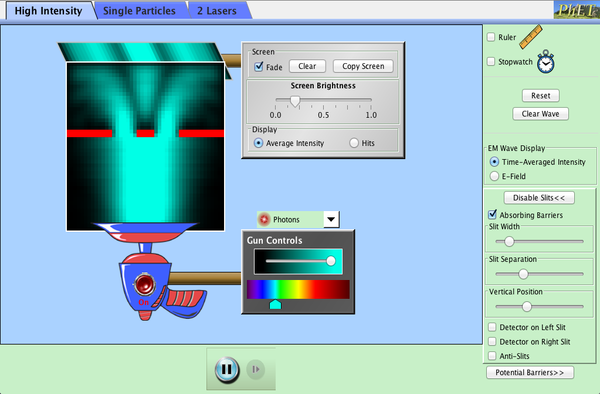
Electron diffraction (see demo below or go to PheT)
|
|
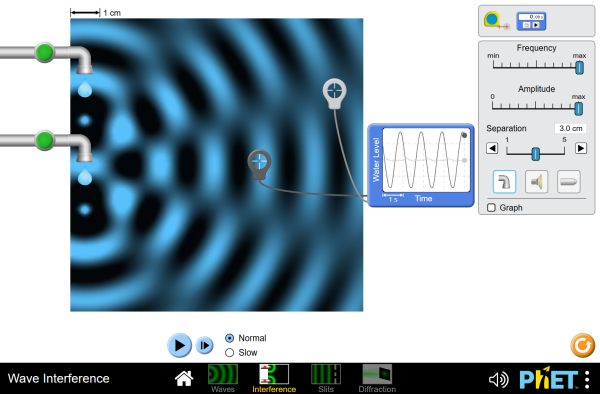
Double-slit experiment (see demo or go to PheT)
|
So what does this mean for atoms? The Bohr model and particle-in-a-box.
Bohr's Model of the Hydrogen Atom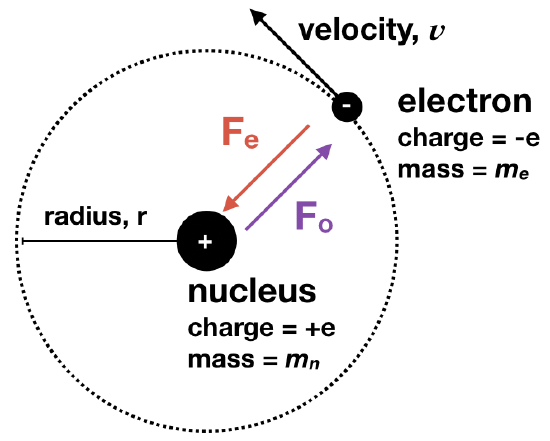
The Danish scientist, Niels Bohr, introduced the first theory that quantized the energy of electrons in atoms. Although Bohr's reasoning relies on classical concepts and hence, is not a correct explanation, the reasoning is interesting, and so we examine this model for its historical significance. This is now referred to as "Old Quantum Theory", while the "New Quantum Theory" is that described by the Schrodinger equation, and that will be described a bit later. Below, the story of Bohr's model will be described. Another way to tell the story is here.
Bohr's Condition of a Stable Orbit: Bohr imagined that electrons were in circular orbit around a nucleus. He applied classical mechanics to rationalize that if the electron of charge, -e, were to be in a stable orbit around a nucleus of opposite charge, +e, then the electrostatic attractive force (Fe) between the electron and nucleus must be exactly opposed by the outward centripetal force (Fo) created by the electron's circular orbit. (We can ignore any gravitational force because it is relatively weak.)
Where the electrostatic attractive force \(F_e\) and centripetal force \(F_o\) are,
\[F_e=\frac{(+e)(-e)}{r^2} = -\frac{e^2}{r^2}\]
\[F_o=\frac{m_ev^2}{r}\]
For a stable orbit to exist \(F_e\) + \(F_o\) = 0, or,
\[F_o = -F_e\]
\[\frac{m_ev^2}{r} = \frac{e^2}{r^2}\]
Bohr's Calculation of the Electron's Energy: Bohr could calculate the total energy of the electron, again using classical mechanics. The total energy of a system is the sum of the kinetic energy (KE, energy of motion of the electron) and the potential energy (PE, from the electrostatic attraction, \(F_e\) and the distance, r).
\[KE = \frac{1}{2}m_ev^2\]
\[PE = rF_e = r\big(-\frac{e^2}{r^2}\big) = -\frac{e^2}{r}\]
If total Energy (E) is equal to the sum of KE and PE,
\[E = KE + PE = \frac{1}{2}m_ev^2 - \frac{e^2}{r}\]
This expression can be simplified by first solving equation (4) for \(m_ev^2=\frac{e^2}{r}\) and substituting into equation 7.
\[E = \frac{1}{2}\big(\frac{e^2}{r}\big)-\frac{2}{2}\big(\frac{e^2}{r}\big) = -\frac{1}{2}\big(\frac{e^2}{r}\big) = -\frac{e^2}{2r}\]
Now we see that energy of the electron, E, can be calculated if we know the distance, r, at which the electron is orbiting. This is a good time to remind ourselves that we also know, from Planck's work, that \(E = h\nu\). This reminds us that the electron is a wave with frequency, \(\nu\), in units of sec-1. So, we could also write,
\[E = -\frac{e^2}{2r} = h\nu\]
Bohr's Quantization, and Equations for Radius, r, and Velocity, v: Bohr knew that electrons must have stable orbits, otherwise the electrons would fall into the nucleus. Bohr was familiar with Maxwell's theory of classical electromagnetism and knew that in a classical theory, the orbiting electron should radiate energy away and eventually collapse into the nucleus (E is given off as r decreases). He circumvented this problem by following Planck's idea underlying blackbody radiation and positing that the orbital angular momentum \(p = m_evr\) of the electron could only take on specific values. He proposed those values to be units of \(\frac{h}{2\pi}\), where h is Planck's constant. Bohr's proposal was,
\[m_evr = n\frac{h}{2\pi}\]
where \(n\) is the first quantum number and can have values of any integer (\(n = 1,2,3...\)). This relationship can be rearranged to find the velocity, \(v\),
\[v = n\frac{h}{m_er2\pi}\]
This implies that only certain velocities are allowed, since only certain values of \(n\) are allowed. This expression for \(v\) can be substituted into the condition of a stable orbit (using a rearranged version of equation 4, (\(m_ev^2=\frac{e^2}{r}\)) to give equation 12. Ultimately, this allows us to find how the radius, \(r\), depends on the the quantum number, \(n\), as shown in equation 13.
\[\frac{m_e\big(n\frac{h}{m_er2\pi}\big)^2}{r} = \frac{m_en^2h^2}{4m_e^2r^2\pi^2} = \frac{n^2h^2}{4m_er^2\pi^2} = \frac{e^2}{r}\]
This expression can be rearranged to solve for \(r\),
\[r = \frac{n^2h^2}{4\pi^2m_ee^2K}\]
K is the Coulomb constant which is needed for unit conversion and has a value of
\(K = 8.9875517923 x 10^9\frac{N m^2}{C^2}\nonumber\)
This expression shows Bohr's assumption that there are discrete distances where the electron can orbit, as the values or \(r\) are restricted by the integer values of \(n\). The relationship between \(n\) and \(E\) is found by substitution of the equation for \(r\) into equation 8 or 9.
\[E = -\frac{e^2K}{2\big(\frac{n^2h^2}{4\pi^2m_ee^2K}\big)} = -\frac{e^2K4\pi^2m_ee^2K}{2n^2h^2} = -\frac{2\pi^2m_ee^42K^2}{n^2h^2}\]
This expression shows that energy is quantized, as like values of \(v\) and \(r\), the energy depends on the integer value, \(n\).
Exercise \(\PageIndex{1}\)
Show how you would find the Bohr radius, velocity, and energy of an electron in the first shell of a hydrogen atom.
- Answer
-
\(r = \frac{n^2h^2}{4\pi^2m_ee^2K}\nonumber\)
\(r = \frac{1^2(6.626070 x 10^{-34})^2}{4(3.141592654)^2(9.10938356 x 10^{-31})(1.602176634 x 10^{-19})^2(8.9875517923 x 10^9)}\nonumber\)
\(r = \frac{(4.390480364 x 10^{-67})J^2s^2}{(8.296805693 x 10^{-57})kg N m^2}\nonumber\)
\(r = 5.292 x 10^{-11}m\nonumber\)
\(v = n\frac{h}{m_er2\pi}\nonumber\)
\(v = 1\frac{6.626070 x 10^{-34}}{(9.10938356 x 10^{-31})(5.292 x 10^{-11})2(3.141592654)}\nonumber\)
\(v = \frac{6.626070 x 10^{-34}Js}{3.028926207 x 10^{-40}kgm}\nonumber\)
\(v = 2.19 x 10^6 m/s\nonumber\)
\(E = -\frac{2\pi^2m_ee^42K^2}{n^2h^2}\nonumber\)
\(E = -\frac{2(3.141592654)^2(9.10938356 x 10^{-31})(1.602176634 x 10^{-19})^4(8.9875517923 x 10^9)^2}{1^2(6.626070 x 10^{-34})^2}\nonumber\)
\(E = -\frac{9.570687085 x 10^{-85}kgN^4m^4}{4.390480367 x 10^{-67}J^2s^2}\nonumber\)
\(E = -2.1799 x 10^{-18} J\nonumber\)
Hydrogen Absorption and Emission Spectra
When a high-voltage electrical discharge is passed through a sample of hydrogen gas (H2) at low pressure, the result is individual isolated hydrogen atoms that emit a red light. Unlike blackbody radiation, the color of the light emitted by the hydrogen atoms does not depend greatly on the temperature of the gas in the tube. When the emitted light is passed through a prism, only a few narrow lines of particular wavelengths, called a line spectrum, are observed rather than a continuous range of wavelengths (Figure \(\PageIndex{1}\)). The light emitted by hydrogen atoms is red because, of its four characteristic lines, the most intense line in its spectrum is in the red portion of the visible spectrum, at 656 nm.
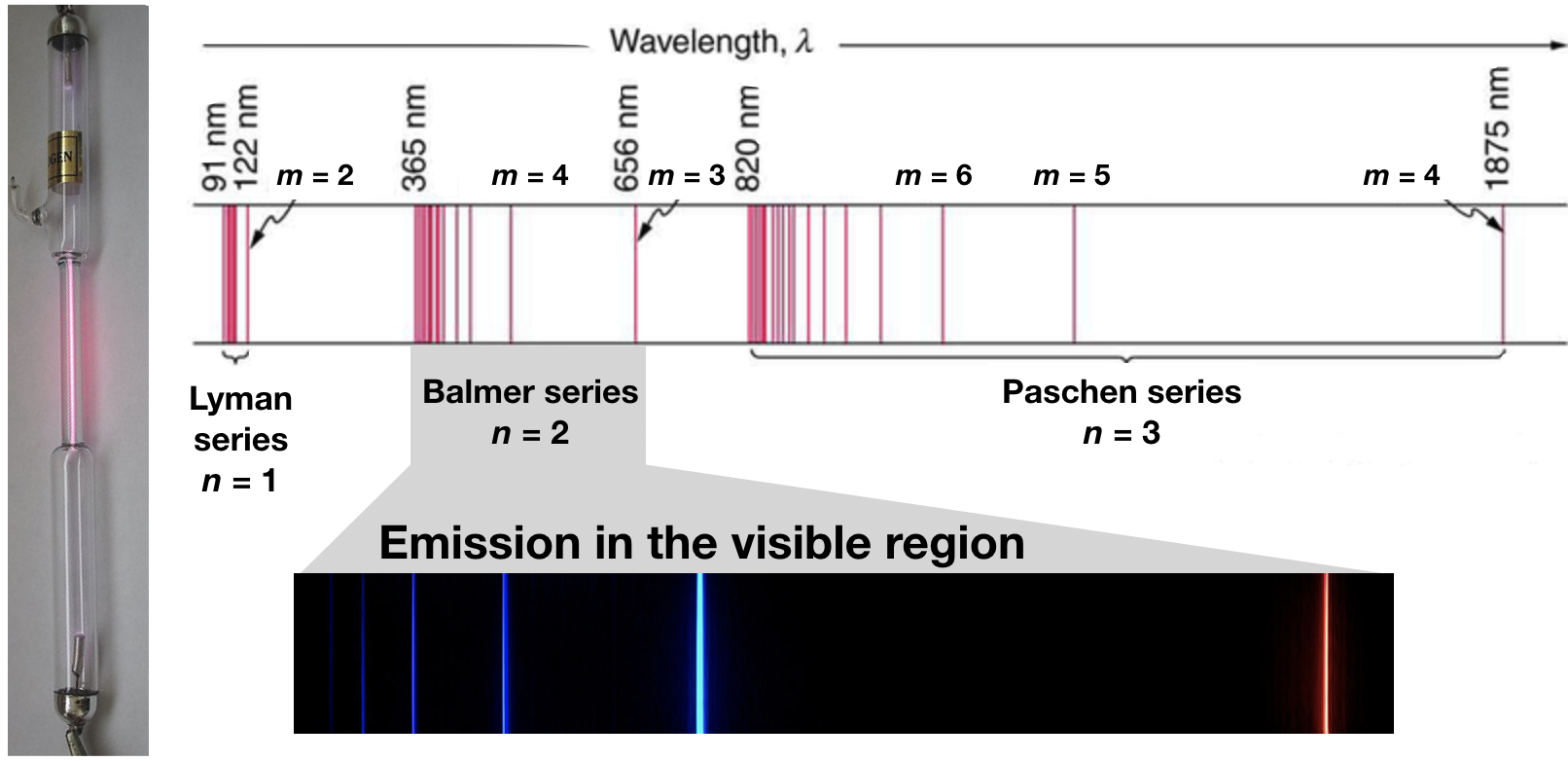
Figure \(\PageIndex{1}\): The Emission of Light by Hydrogen Atoms. (left) A sample of excited hydrogen atoms emits a characteristic red light. (bottom) When the light emitted by a sample of excited hydrogen atoms is split into its component wavelengths by a prism, four characteristic violet, blue, green, and red emission lines can be observed, the most intense of which is at 656 nm. (top) An diagram showing extended regions of the electromagnetic spectrum and the hydrogen line spectra that are observed.
In 1885, a Swiss mathematics teacher, Johann Balmer (1825–1898), showed that the frequencies of the lines observed in the visible region of the hydrogen line spectrum fit a simple equation that can be expressed as follows:
\[ \nu=constant\; \left ( \dfrac{1}{2^{2}}-\dfrac{1}{n^{^{2}}} \right ) \label{6.3.1}\]
where n = 3, 4, 5, 6. As a result, these lines are known as the Balmer series. The Swedish physicist Johannes Rydberg (1854–1919) subsequently restated and expanded Balmer’s result in the Rydberg equation:
\[ \dfrac{1}{\lambda }=R_h\; \left ( \dfrac{1}{n^{2}}-\dfrac{1}{m^{2}} \right ) \label{6.3.2}\]
where \(n\) and \(m\) are positive integers, \(m > n\), and \(R_h\) the Rydberg constant, has a value of 1.09737 × 107 m−1. Like Balmer’s equation, Rydberg’s simple equation described the wavelengths of the visible lines in the emission spectrum of hydrogen (with n = 2, m = 3, 4, 5,…). More important, Rydberg’s equation also predicted the wavelengths of other series of lines that would be observed in the emission spectrum of hydrogen: one in the ultraviolet (n = 1, m = 2, 3, 4,…) and one in the infrared (n = 3, m = 4, 5, 6).
Exercise \(\PageIndex{2}\)
Solve the Rydberg Equation for a line where \(m = 3\) and \(n = 1\). In what region of the electromagnetic spectrum does this appear, and which series is this?
- Answer
-
\(\frac{1}{\lambda } = R_h\left(\dfrac{1}{n^{2}}-\dfrac{1}{m^{2}}\right)\nonumber\)
\(\frac{1}{\lambda } = 1.09737 x 10^7m^{-1}\left(\dfrac{1}{1^{2}}-\dfrac{1}{3^{2}}\right)\nonumber\)
\(\frac{1}{\lambda } = 9754400m^{-1}\nonumber\)
\({\lambda } = 1.03 x 10^{-7}m = 102.5 nm\nonumber\)
This is in the Ultra-violet region.