1.2: Rutherford's Atom
- Page ID
- 294735
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
Learning Objectives
- Introduce the initial attempts to explain the structure of atoms.
The Gold Foil Experiment
In 1911, Rutherford and coworkers Hans Geiger and Ernest Marsden initiated a series of groundbreaking experiments that would completely change the accepted model of the atom. They bombarded very thin sheets of gold foil with fast moving alpha particles. Alpha particles, a type of natural radioactive particle, are positively charged particles with a mass about four times that of a hydrogen atom.
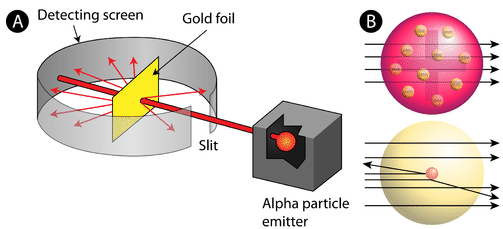
According to the accepted atomic model, in which an atom's mass and charge are uniformly distributed throughout the atom, the scientists expected that all of the alpha particles would pass through the gold foil with only a slight deflection or none at all. Surprisingly, while most of the alpha particles were indeed undeflected, a very small percentage (about 1 in 8000 particles) bounced off the gold foil at very large angles. Some were even redirected back toward the source. No prior knowledge had prepared them for this discovery. In a famous quote, Rutherford exclaimed that it was "as if you had fired a 15-inch [artillery] shell at a piece of tissue and it came back and hit you."
Rutherford needed to come up with an entirely new model of the atom in order to explain his results. Because the vast majority of the alpha particles had passed through the gold, he reasoned that most of the atom was empty space. In contrast, the particles that were highly deflected must have experienced a tremendously powerful force within the atom. He concluded that all of the positive charge and the majority of the mass of the atom must be concentrated in a very small space in the atom's interior, which he called the nucleus. The nucleus is the tiny, dense, central core of the atom and is composed of protons and neutrons.
Rutherford's atomic model became known as the nuclear model. Most of the \(\alpha\)-particles were not scattered; they passed unchanged through the thin metal foil. Some of the few that were scattered were scattered in the backward direction; i.e. they recoiled. This backward scattering requires that the foil contain heavy particles. When an α-particle hits one of these heavy particles it simply recoils backward, just like a ball thrown at a brick wall. Since most of the \(\alpha\)-particles don’t get scattered, the heavy particles (the nuclei of the atoms) must occupy only a very small region of the total space of the atom. Most of the space must be empty or occupied by very low-mass particles. These low-mass particles are the electrons that surround the nucleus. It is worth emphasizing just how small the nucleus is compared to the rest of the atom. If we could blow up an atom to be the size of a large professional football stadium, the nucleus would be about the size of a marble.
Rutherford's Failed Planetary Atom
There are some basic problems with the Rutherford model. The Coulomb force that exists between oppositely charge particles means that a positive nucleus and negative electrons should attract each other, and the atom should collapse. To prevent the collapse, the electron was postulated to be orbiting the positive nucleus. The Coulomb force (discussed below) is used to change the direction of the velocity, just as a string pulls a ball in a circular orbit around your head or the gravitational force holds the moon in orbit around the Earth. The origin for this hypothesis that suggests this perspective is plausible is the similarity of gravity and Coulombic interactions. The expression for the force of gravity between two masses (Newton's Law of gravity) is
\[F_{gravity} \propto \dfrac{m_1m_2}{r^2}\label{1.8.1}\]
with \(m_1\) and \(m_2\) representing the mass of object 1 and 2, respectively and \(r\) representing the distance between the objects centers
The expression for the Coulomb force between two charged species is
\[F_{Coulomb} \propto \dfrac{Q_1Q_2}{r^2}\label{1.8.2}\]
with \(Q_1\) and \(Q_2\) representing the charge of object 1 and 2, respectively and \(r\) representing the distance between the objects centers.
However, this analogy has a problem too. An electron going around in a circle is constantly being accelerated because its velocity vector is changing. A charged particle that is being accelerated emits radiation. This property is essentially how a radio transmitter works. A power supply drives electrons up and down a wire and thus transmits energy (electromagnetic radiation) that your radio receiver picks up. The radio then plays the music for you that is encoded in the waveform of the radiated energy.
If the orbiting electron is generating radiation, it is losing energy. If an orbiting particle loses energy, the radius of the orbit decreases. To conserve angular momentum, the frequency of the orbiting electron increases. The frequency increases continuously as the electron collapses toward the nucleus. Since the frequency of the rotating electron and the frequency of the radiation that is emitted are the same, both change continuously to produce a continuous spectrum and not the observed discrete lines. Furthermore, if one calculates how long it takes for this collapse to occur, one finds that it takes about \(10^{‑1l}\) seconds. This means that nothing in the world based on the structure of atoms could exist for longer than about \(10^{-11}\) seconds. Clearly something is terribly wrong with this classical picture, which means that something was missing at that time from the known laws of physics.
Conservative Forces can be explained with Potentials
A conservative force is dependent only on the position of the object. If a force is conservative, it is possible to assign a numerical value for the potential at any point. When an object moves from one location to another, the force changes the potential energy of the object by an amount that does not depend on the path taken. The potential can be constructed as simple derivatives for 1-D forces:
\[F = -\dfrac{dV}{dx} \nonumber\]
or as gradients in 3-D forces
\[F = -\nabla V \nonumber\]
where \(\nabla\) is the vector of partial derivatives
\[\nabla = \left ( \dfrac{\partial}{\partial x}, \dfrac{\partial}{\partial y}, \dfrac{\partial}{\partial z} \right) \nonumber\]
The most familiar conservative forces are gravity and Coloumbic forces.
The Coulomb force law (Equation \(\ref{1.8.2}\)) comes from the corresponding Coulomb potential (sometimes call electrostatic potential)
\[V(r)=\dfrac{kQ_1 Q_2}{r} \label{1.8.5}\]
and it can be easily verified that the Coulombic force from this interaction (\(F(r)\) is
\[F(r)=-\dfrac{dV}{dr} \label{1.8.6}\]
As \(r\) is varied, the energy will change, so that we have an example of a potential energy curve \(V(r)\) (Figure \(\PageIndex{2; left}\)). If \(Q_1\) and \(Q_2\) are the same sign, then the curve which is a purely repulsive potential, i.e., the energy increases monotonically as the charges are brought together and decreases monotonically as they are separated. From this, it is easy to see that like charges (charges of the same sign) repel each other.
If the charges are of opposite sign, then the curve appears roughly Figure \(\PageIndex{2; right}\) and this is a purely attractive potential. Thus, the energy decreases as the charges are brought together, implying that opposite charges attract.
Contributors and Attributions
- CK-12 Foundation by Sharon Bewick, Richard Parsons, Therese Forsythe, Shonna Robinson, and Jean Dupon.
David M. Hanson, Erica Harvey, Robert Sweeney, Theresa Julia Zielinski ("Quantum States of Atoms and Molecules")
- Template:Contriboundless

