Chapter 4.2: Lattice Energies in Ionic Solids
- Page ID
- 17557
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)
Learning Objectives
- To understand the relationship between the lattice energy and physical properties of an ionic compound.
The reaction of a metal with a nonmetal usually produces an ionic compound; that is, electrons are transferred from the metal to the nonmetal. Metal ores are commonly combinations of metal atoms with oxygen atoms, and this combination is produced when metals rust, so the process where electrons are transferred to the oxygen atoms from the metal atoms is known as oxidation of the metal and the reverse process, where pure metals are produced is called reduction of the ore to the metal.
Ionic compounds are usually rigid, brittle, crystalline substances with flat surfaces that intersect at characteristic angles. They are not easily deformed, and they melt at relatively high temperatures. NaCl, for example, melts at 801°C. These properties result from the regular arrangement of the ions in the crystalline lattice and from the strong electrostatic attractive forces between ions with opposite charges.
While Equation 4.1.1 has demonstrated that the formation of ion pairs from isolated ions releases large amounts of energy, even more energy is released when these ion pairs condense to form an ordered three-dimensional array. In such an arrangement each cation in the lattice is surrounded by more than one anion (typically four, six, or eight) and vice versa, so it is more stable than a system consisting of separate pairs of ions, in which there is only one cation–anion interaction in each pair. Note that r0 may differ between the gas-phase dimer and the lattice.
Note the Pattern
An ionic lattice is more stable than a system consisting of separate ion pairs.
Calculating Lattice Energies
The lattice energy of nearly any ionic solid can be calculated rather accurately using a modified form of Equation 4.1:
\( U = - k^{\prime} \dfrac {Q_{1}Q_{2}}{r_{0}},\; where\; U > 0 \tag{4.2.1} \)
U, which is always a positive number, represents the amount of energy required to dissociate 1 mol of an ionic solid into the gaseous ions. As before, Q1 and Q2 are the charges on the ions and r0 is the internuclear distance. We see from Equation 4.4 that lattice energy is directly related to the product of the ion charges and inversely related to the internuclear distance. The value of the constant k′ depends on the specific arrangement of ions in the solid lattice and their valence electron configurations, topics that will be discussed in more detail in the second semester. Representative values for calculated lattice energies, which range from about 600 to 10,000 kJ/mol, are listed in Table 4.2.1. Energies of this magnitude can be decisive in determining the chemistry of the elements.
Table 4.2.1 Representative Calculated Lattice Energies
| Substance | U (kJ/mol) |
|---|---|
| NaI | 682 |
| CaI2 | 1971 |
| MgI2 | 2293 |
| NaOH | 887 |
| Na2O | 2481 |
| NaNO3 | 755 |
| Ca3(PO4)2 | 10,602 |
| CaCO3 | 2804 |
Source: Data from CRC Handbook of Chemistry and Physics (2004).
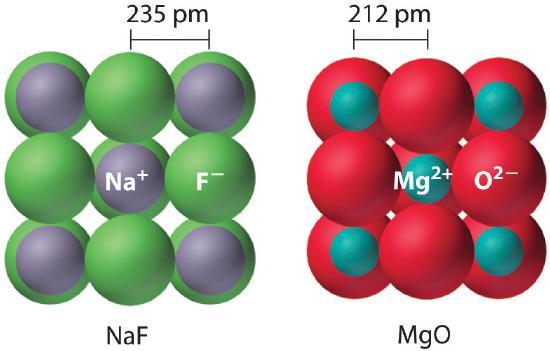
Because the lattice energy depends on the product of the charges of the ions, a salt having a metal cation with a +2 charge (M2+) and a nonmetal anion with a −2 charge (X2−) will have a lattice energy four times greater than one with M+ and X−, assuming the ions are of comparable size (and have similar internuclear distances). For example, the calculated value of U for NaF is 910 kJ/mol, whereas U for MgO (containing Mg2+ and O2− ions) is 3795 kJ/mol.
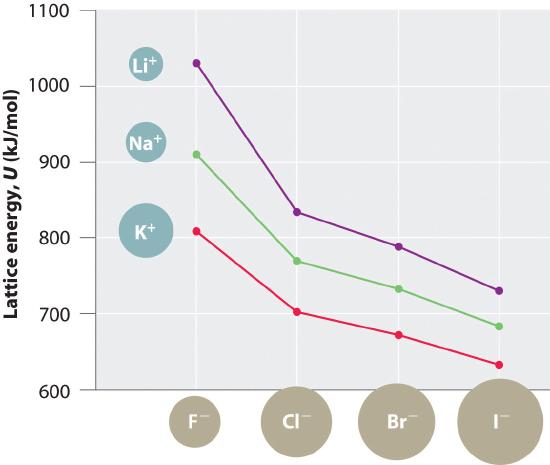
Because lattice energy is inversely related to the internuclear distance, it is also inversely proportional to the size of the ions. This effect is illustrated in Figure 4.2.2, which shows that lattice energy decreases for the series LiX, NaX, and KX as the radius of X− increases. Because r0 in Equation 4.2.1 is the sum of the ionic radii of the cation and the anion (r0 = r+ + r−), r0 increases as the cation becomes larger in the series, so the magnitude of U decreases. A similar effect is seen when the anion becomes larger in a series of compounds with the same cation.
Figure 4.2.2 A Plot of Lattice Energy versus the Identity of the Halide for the Lithium, Sodium, and Potassium Halides. Because the ionic radii of the cations decrease in the order K+ > Na+ > Li+ for a given halide ion, the lattice energy decreases smoothly from Li+ to K+. Conversely, for a given alkali metal ion, the fluoride salt always has the highest lattice energy and the iodide salt the lowest.
Note the Pattern
Lattice energies are highest for substances with small, highly charged ions.
Example 2
Arrange GaP, BaS, CaO, and RbCl in order of increasing lattice energy.
Given: four compounds
Asked for: order of increasing lattice energy
Strategy:
Using Equation 4.2.1, predict the order of the lattice energies based on the charges on the ions. For compounds with ions with the same charge, use the relative sizes of the ions to make this prediction.
Solution:
The compound GaP, which is used in semiconductor electronics, contains Ga3+ and P3− ions; the compound BaS contains Ba2+ and S2− ions; the compound CaO contains Ca2+ and O2− ions; and the compound RbCl has Rb+ and Cl− ions. We know from Equation 4.4 that lattice energy is directly proportional to the product of the ionic charges. Consequently, we expect RbCl, with a (−1)(+1) term in the numerator, to have the lowest lattice energy, and GaP, with a (+3)(−3) term, the highest. To decide whether BaS or CaO has the greater lattice energy, we need to consider the relative sizes of the ions because both compounds contain a +2 metal ion and a −2 chalcogenide ion. Because Ba2+ lies below Ca2+ in the periodic table, Ba2+ is larger than Ca2+. Similarly, S2− is larger than O2−. Because the cation and the anion in BaS are both larger than the corresponding ions in CaO, the internuclear distance is greater in BaS and its lattice energy will be lower than that of CaO. The order of increasing lattice energy is RbCl < BaS < CaO < GaP.
Exercise
Arrange InAs, KBr, LiCl, SrSe, and ZnS in order of decreasing lattice energy.
Answer: InAs > ZnS > SrSe > LiCl > KBr
The Relationship between Lattice Energies and Physical Properties
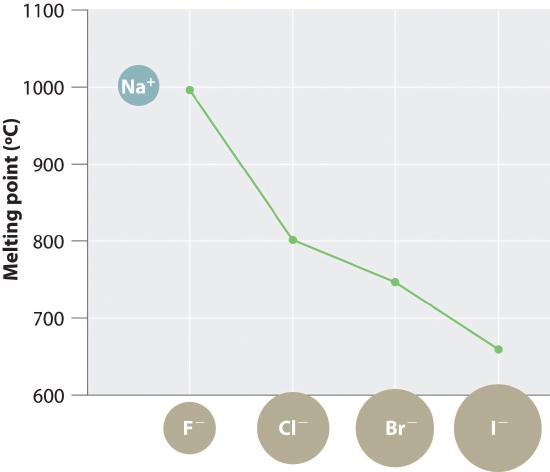
The magnitude of the forces that hold an ionic substance together has a dramatic effect on many of its properties. The melting point is the temperature at which the individual ions in a lattice or the individual molecules in a covalent compound have enough kinetic energy to overcome the attractive forces that hold them together in the solid. At the melting point, the ions can move freely, and the substance becomes a liquid. Thus melting points vary with lattice energies for ionic substances that have similar structures. The melting points of the sodium halides (Figure 4.2.3), for example, decrease smoothly from NaF to NaI, following the same trend as seen for their lattice energies (Figure 4.2.2). Similarly, the melting point of MgO is 2825°C, compared with 996°C for NaF, reflecting the higher lattice energies associated with higher charges on the ions. In fact, because of its high melting point, MgO is used as an electrical insulator in heating elements for electric stoves.
Figure 4.2.3 A Plot of Melting Point versus the Identity of the Halide for the Sodium Halides. The melting points follow the same trend as the magnitude of the lattice energies in Figure 4.2.2.
The hardness s the resistance of ionic materials to scratching or abrasion. of ionic materials—that is, their resistance to scratching or abrasion—is also related to their lattice energies. Hardness is directly related to how tightly the ions are held together electrostatically, which, as we saw, is also reflected in the lattice energy. As an example, MgO is harder than NaF, which is consistent with its higher lattice energy.
In addition to determining melting point and hardness, lattice energies affect the solubilities of ionic substances in water. In general, the higher the lattice energy, the less soluble a compound is in water. For example, the solubility of NaF in water at 25°C is 4.13 g/100 mL, but under the same conditions, the solubility of MgO is only 0.65 mg/100 mL, meaning that it is essentially insoluble.
Note the Pattern
High lattice energies lead to hard, insoluble compounds with high melting points.
Summary
Ionic compounds have strong electrostatic attractions between oppositely charged ions in a regular array. The lattice energy (U) of an ionic substance is defined as the energy required to dissociate the solid into gaseous ions; U can be calculated from the charges on the ions, the arrangement of the ions in the solid, and the internuclear distance. Because U depends on the product of the ionic charges, substances with di- or tripositive cations and/or di- or trinegative anions tend to have higher lattice energies than their singly charged counterparts. Higher lattice energies typically result in higher melting points and increased hardness because more thermal energy is needed to overcome the forces that hold the ions together.
Key Takeaway
- The lattice energy is usually the most important energy factor in determining the stability of an ionic compound.
Key Equation
Lattice energy
\[ U=-k^{\prime} \dfrac {Q_{1}Q_{2}}{r_{0}} \tag{4.2.1}\]
Conceptual Problems
-
If a great deal of energy is required to form gaseous ions, why do ionic compounds form at all?
-
What are the general physical characteristics of ionic compounds?
-
Ionic compounds consist of crystalline lattices rather than discrete ion pairs. Why?
-
What factors affect the magnitude of the lattice energy of an ionic compound? What is the relationship between ionic size and lattice energy?
-
Which would have the larger lattice energy—an ionic compound consisting of a large cation and a large anion or one consisting of a large anion and a small cation? Explain your answer and any assumptions you made.
-
How would the lattice energy of an ionic compound consisting of a monovalent cation and a divalent anion compare with the lattice energy of an ionic compound containing a monovalent cation and a monovalent anion, if the internuclear distance was the same in both compounds? Explain your answer.
-
Which would have the larger lattice energy—CrCl2 or CrCl3—assuming similar arrangements of ions in the lattice? Explain your answer.
-
Which cation in each pair would be expected to form a chloride salt with the larger lattice energy, assuming similar arrangements of ions in the lattice? Explain your reasoning.
- Na+, Mg2+
- Li+, Cs+
- Cu+, Cu2+
-
Which cation in each pair would be expected to form an oxide with the higher melting point, assuming similar arrangements of ions in the lattice? Explain your reasoning.
- Mg2+, Sr2+
- Cs+, Ba2+
- Fe2+, Fe3+
Numerical Problems
-
Arrange SrO, PbS, and PrI3 in order of decreasing lattice energy.
-
Compare BaO and MgO with respect to each of the following properties.
- enthalpy of sublimation
- ionization energy of the metal
- lattice energy
- enthalpy of formation