2: Oxidation Numbers and Redox Reactions

Redox reactions may involve proton transfers and other bond-breaking and bond-making processes, as well as electron transfers, and therefore the equations involved are much more difficult to deal with than those describing acid-base reactions. In order to be able to recognize redox reactions, we need a method for keeping a careful account of all the electrons. This is done by assigning oxidation numbers to each atom before and after the reaction.

For example, in NO₃^– the nitrogen is assigned an oxidation number of +5 and each oxygen an oxidation number of –2. This arbitrary assignment corresponds to the nitrogen’s having lost its original five valence electrons to the electronegative oxygens. In NO₂, on the other hand, the nitrogen has an oxidation number of + 4 and may be thought of as having one valence electron for itself, that is, one more electron than it had in NO₃^–.

This arbitrarily assigned gain of one electron corresponds to reduction of the nitrogen atom on going from NO₃^– to NO₂. As a general rule, reduction corresponds to a lowering of the oxidation number of some atom. Oxidation corresponds to increasing the oxidation number of some atom. Applying the oxidation number rules to the following equation, we have

Since the oxidation number of copper increased from 0 to +2, we say that copper was oxidized and lost two negatively charged electrons. The oxidation number of nitrogen went down from 5 to 4, and so the nitrogen (or nitrate ion) was reduced. Each nitrogen gained one electron, so 2e^– were needed for the 2 NO₃^–. The nitrogen was reduced by electrons donated by copper, and so copper was the reducing agent. Copper was oxidized because its electrons were accepted by an oxidizing agent, nitrogen (or nitrate ion).

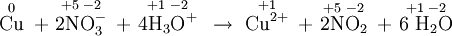
Although they are useful and necessary for recognizing redox reactions, oxidation numbers are a highly artificial device. The nitrogen atom in NO₃^– does not really have a +5 charge which can be reduced to +4 in NO₂. Instead, there are covalent bonds and electron-pair sharing between nitrogen and oxygen in both species, and nitrogen has certainly not lost its valence electrons entirely to oxygen. Even though this may (and indeed should) make you suspicious of the validity of oxidation numbers, they are undoubtedly a useful tool for spotting electron-transfer processes. So long as they are used for that purpose only, and not taken to mean that atoms in covalent species actually have the large charges oxidation numbers often imply, their use is quite valid.

The general rules for oxidation numbers are seen below, taken from the following page in the Analytical Chemistry Core Textbook: Oxidation States

Determining Oxidation States

Counting the number of electrons transferred is an inefficient and time-consuming way of determining oxidation states.These rules provide a simpler method:

• The oxidation state of an uncombined element is zero. This applies regardless of the structure of the element: Xe, Cl_2, S₈, and large structures of carbon or silicon each have an oxidation state of zero.
• The sum of the oxidation states of all the atoms or ions in a neutral compound is zero.
• The sum of the oxidation states of all the atoms in an ion is equal to the charge on the ion.
• The more electronegative element in a substance is assigned a negative oxidation state. The less electronegative element is assigned a positive oxidation state. Remember that electronegativity is greatest at the top-right of the periodic table and decreases toward the bottom-left.
• Some elements almost always have the same oxidation states in their compounds:

Element	Usual oxidation state	Exceptions
Group 1 metals	Always +1
Group 2 metals	Always +2
Oxygen	Usually -2	Peroxides and F2O (see below)
Hydrogen	Usually +1	Metal hydrides (-1) (see below)
Fluorine	Always -1
Chlorine	usually -1	Compounds with O or F (see below)

Exceptions:

Hydrogen in the metal hydrides: Metal hydrides include compounds like sodium hydride, NaH. Here the hydrogen exists as a hydride ion, H^-. The oxidation state of a simple ion like hydride is equal to the charge on the ion—in this case, -1.

Alternatively, the sum of the oxidation states in a neutral compound is zero. Because Group 1 metals always have an oxidation state of +1 in their compounds, it follows that the hydrogen must have an oxidation state of -1 (+1 -1 = 0).

Oxygen in peroxides: Peroxides include hydrogen peroxide, H₂O₂. This is an electrically neutral compound, so the sum of the oxidation states of the hydrogen and oxygen must be zero.

Because each hydrogen has an oxidation state of +1, each oxygen must have an oxidation state of -1 to balance it.

Oxygen in F₂O: The deviation here stems from the fact that oxygen is less electronegative than fluorine; the fluorine takes priority with an oxidation state of -1. Because the compound is neutral, the oxygen has an oxidation state of +2.

Chlorine in compounds with fluorine or oxygen: Because chlorine adopts such a wide variety of oxidation states in these compounds, it is safer to simply remember that its oxidation state is not -1, and work the correct state out using fluorine or oxygen as a reference.

Example \(\PageIndex{1}\) : Redox Reactions

Identify the redox reactions and the reducing and oxidizing agents from the following:

1. \(\ce{2MnO4^{–} + 5SO2 + 6H2O -> 5SO4^{2–} + 2Mn^{2+} + 4H3O^{+}}\)
2. \(\ce{NH4^+ + PO4^{3–} -> NH3 + PO4^{2–}}\)
3. \(\ce{HClO + H2S -> H3O^+ + Cl^{–} + S}\)

Solution:

a) The appropriate oxidation numbers are

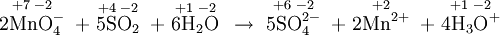The only atoms which change are Mn, from +7 to +2, a reduction, and S, from +4 to +6, an oxidation. The reaction is a redox process. SO₂ has been oxidized by MnO₄^–, and so MnO₄^–is the oxidizing agent. MnO₄^– has been reduced by SO₂, and so SO₂ is the reducing agent.

b) The oxidation numbers

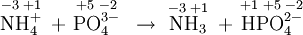
show that no redox has occurred. This is an acid-base reaction because a proton, but no electrons, has been transferred.

c)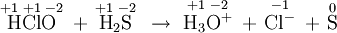

H₂S has been oxidized, losing two electrons to form elemental S. Since H₂S donates electrons, it is the reducing agent. HClO accepts these electrons and is reduced to Cl^–. Since it accepts electrons, HClO is the oxidizing agent.

Contributors

• Ed Vitz (Kutztown University), John W. Moore (UW-Madison), Justin Shorb (Hope College), Xavier Prat-Resina (University of Minnesota Rochester), Tim Wendorff, and Adam Hahn.