12.2: The Solution Process

Learning Objectives

• To understand how enthalpy and entropy changes affect solution formation.
• To use the magnitude of the changes in both enthalpy and entropy to predict whether a given solute–solvent combination will spontaneously form a solution.

In all solutions, whether gaseous, liquid, or solid, the substance present in the greatest amount is the solvent, and the substance or substances present in lesser amounts are the solute(s). The solute does not have to be in the same physical state as the solvent, but the physical state of the solvent usually determines the state of the solution. As long as the solute and solvent combine to give a homogeneous solution, the solute is said to be soluble in the solvent. Table \(\PageIndex{1}\) lists some common examples of gaseous, liquid, and solid solutions and identifies the physical states of the solute and solvent in each.

Table \(\PageIndex{1}\): Types of Solutions

Solution	Solute	Solvent	Examples
gas	gas	gas	air, natural gas
liquid	gas	liquid	seltzer water (\(CO_2\) gas in water)
liquid	liquid	liquid	alcoholic beverage (ethanol in water), gasoline
liquid	solid	liquid	tea, salt water
solid	gas	solid	\(H_2\) in Pd (used for \(H_2\) storage)
solid	solid	liquid	mercury in silver or gold (amalgam often used in dentistry)
solid	solid	solid	alloys and other "solid solutions"

Forming a Solution

The formation of a solution from a solute and a solvent is a physical process, not a chemical one. That is, both solute and solvent can be recovered in chemically unchanged forms using appropriate separation methods. For example, solid zinc nitrate dissolves in water to form an aqueous solution of zinc nitrate:

\[\ce{Zn(NO3)2(s) + H2O(l) \rightarrow Zn^{2+}(aq) + 2NO^{-}3(aq)} \label{13.1.1} \]

Because \(Zn(NO_3)_2\) can be recovered easily by evaporating the water, this is a physical process. In contrast, metallic zinc appears to dissolve in aqueous hydrochloric acid. In fact, the two substances undergo a chemical reaction to form an aqueous solution of zinc chloride with evolution of hydrogen gas:

\[\ce{ Zn(s) + 2H^{+}(aq) + 2Cl^{-}(aq) \rightarrow Zn^{2+}(aq) + 2Cl^{-}(aq) + H2(g)} \label{13.1.2} \]

When the solution evaporates, we do not recover metallic zinc, so we cannot say that metallic zinc is soluble in aqueous hydrochloric acid because it is chemically transformed when it dissolves. The dissolution of a solute in a solvent to form a solution does not involve a chemical transformation (that it is a physical change).

Dissolution of a solute in a solvent to form a solution does not involve a chemical transformation.

Substances that form a single homogeneous phase in all proportions are said to be completely miscible in one another. Ethanol and water are miscible, just as mixtures of gases are miscible. If two substances are essentially insoluble in each other, such as oil and water, they are immiscible. Examples of gaseous solutions that we have already discussed include Earth’s atmosphere.

The Role of Enthalpy in Solution Formation

Energy is required to overcome the intermolecular interactions in a solute, which can be supplied only by the new interactions that occur in the solution, when each solute particle is surrounded by particles of the solvent in a process called solvation (or hydration when the solvent is water). Thus all of the solute–solute interactions and many of the solvent–solvent interactions must be disrupted for a solution to form. In this section, we describe the role of enthalpy in this process.

Because enthalpy is a state function, we can use a thermochemical cycle to analyze the energetics of solution formation. The process occurs in three discrete steps, indicated by \(ΔH_1\), \(ΔH_2\), and \(ΔH_3\) in Figure \(\PageIndex{2}\). The overall enthalpy change in the formation of the solution (\( \Delta H_{soln}\)) is the sum of the enthalpy changes in the three steps:

\[ \Delta H_{soln} = \Delta H_1 + \Delta H_2 + \Delta H_3 \label{13.1.3} \]

When a solvent is added to a solution, steps 1 and 2 are both endothermic because energy is required to overcome the intermolecular interactions in the solvent (\(\Delta H_1\)) and the solute (\(\Delta H_2\)). Because \(ΔH\) is positive for both steps 1 and 2, the solute–solvent interactions (\(\Delta H_3\)) must be stronger than the solute–solute and solvent–solvent interactions they replace in order for the dissolution process to be exothermic (\(\Delta H_{soln} < 0\)). When the solute is an ionic solid, \(ΔH_2\) corresponds to the lattice energy that must be overcome to form a solution. The higher the charge of the ions in an ionic solid, the higher the lattice energy. Consequently, solids that have very high lattice energies, such as \(MgO\) (−3791 kJ/mol), are generally insoluble in all solvents.

Figure \(\PageIndex{2}\): Enthalpy Changes That Accompany the Formation of a Solution. Solvation can be an exothermic or endothermic process depending on the nature of the solute and solvent. In both cases, step 1, separation of the solvent particles, is energetically uphill (ΔH₁ > 0), as is step 2, separation of the solute particles (ΔH₂ > 0). In contrast, energy is released in step 3 (\(ΔH_3\) < 0) because of interactions between the solute and solvent. (a) When \(ΔH_3\) is larger in magnitude than the sum of \(ΔH_1\) and \(ΔH_2\), the overall process is exothermic (\(ΔH_{soln}\) < 0), as shown in the thermochemical cycle. (b) When \(ΔH_3\) is smaller in magnitude than the sum of \(ΔH_1\) and \(ΔH_2\), the overall process is endothermic (\(ΔH_{soln}\) > 0).

A positive value for \(ΔH_{soln}\) does not mean that a solution will not form. Whether a given process, including formation of a solution, occurs spontaneously depends on whether the total energy of the system is lowered as a result. Enthalpy is only one of the contributing factors. A high \(ΔH_{soln}\) is usually an indication that the substance is not very soluble. Instant cold packs used to treat athletic injuries, for example, take advantage of the large positive \(ΔH_{soln}\) of ammonium nitrate during dissolution (+25.7 kJ/mol), which produces temperatures less than 0°C (Figure \(\PageIndex{3}\)).

Figure \(\PageIndex{3}\): Commercial Cold Packs for Treating Injuries. These packs contain solid \(NH_4NO_3\) and water in separate compartments. When the seal between the compartments is broken, the \(NH_4NO_3\) dissolves in the water. Because \(ΔH_{soln}\) for \(NH_4NO_3\) is much greater than zero, heat is absorbed by the cold pack during the dissolution process, producing local temperatures less than 0°C.

Entropy and Solution Formation

The enthalpy change that accompanies a process is important because processes that release substantial amounts of energy tend to occur spontaneously. A second property of any system, its entropy, is also important in helping us determine whether a given process occurs spontaneously. We will discuss entropy in more detail elsewhere, but for now we can state that entropy (\(S\)) is a thermodynamic property of all substances that is proportional to their degree of disorder. A perfect crystal at 0 K, whose atoms are regularly arranged in a perfect lattice and are motionless, has an entropy of zero. In contrast, gases have large positive entropies because their molecules are highly disordered and in constant motion at high speeds.

The formation of a solution disperses molecules, atoms, or ions of one kind throughout a second substance, which generally increases the disorder and results in an increase in the entropy of the system. Thus entropic factors almost always favor formation of a solution. In contrast, a change in enthalpy may or may not favor solution formation. The London dispersion forces that hold cyclohexane and n-hexane together in pure liquids, for example, are similar in nature and strength. Consequently, \(ΔH_{soln}\) should be approximately zero, as is observed experimentally. Mixing equal amounts of the two liquids, however, produces a solution in which the n-hexane and cyclohexane molecules are uniformly distributed over approximately twice the initial volume. In this case, the driving force for solution formation is not a negative \(ΔH_{soln}\) but rather the increase in entropy due to the increased disorder in the mixture. All spontaneous processes with \(ΔH \ge 0\) are characterized by an increase in entropy. In other cases, such as mixing oil with water, salt with gasoline, or sugar with hexane, the enthalpy of solution is large and positive, and the increase in entropy resulting from solution formation is not enough to overcome it. Thus in these cases a solution does not form.

All spontaneous processes with ΔH ≥ 0 are characterized by an increase in entropy.

Table \(\PageIndex{2}\) summarizes how enthalpic factors affect solution formation for four general cases. The column on the far right uses the relative magnitudes of the enthalpic contributions to predict whether a solution will form from each of the four. Keep in mind that in each case entropy favors solution formation. In two of the cases the enthalpy of solution is expected to be relatively small and can be either positive or negative. Thus the entropic contribution dominates, and we expect a solution to form readily. In the other two cases the enthalpy of solution is expected to be large and positive. The entropic contribution, though favorable, is usually too small to overcome the unfavorable enthalpy term. Hence we expect that a solution will not form readily.

Table \(\PageIndex{2}\): Relative Changes in Enthalpies for Different Solute–Solvent Combinations*

\(ΔH_1\) (separation of solvent molecules)	\(ΔH_2\) (separation of solute particles)	\(ΔH_3\) (solute–solvent interactions)	\(ΔH_{soln}\) (\(ΔH_1\) + \(ΔH_2\) +\(ΔH_3\))	Result of Mixing Solute and Solvent†
large; positive	large; positive	large; negative	small; positive or negative	solution will usually form
small; positive	large; positive	small; negative	large; positive	solution will not form
large; positive	small; positive	small; negative	large; positive	solution will not form
small; positive	small; positive	small; negative	small; positive or negative	solution will usually form
*\(ΔH_1\), \(ΔH_2\), and \(ΔH_3\) refer to the processes indicated in the thermochemical cycle shown in Figure \(\PageIndex{2}\). ^†In all four cases, entropy increases.

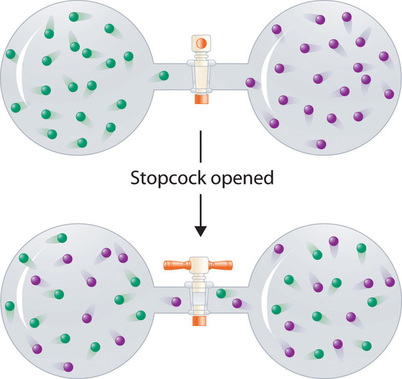
In contrast to liquid solutions, the intermolecular interactions in gases are weak (they are considered to be nonexistent in ideal gases). Hence mixing gases is usually a thermally neutral process (\(ΔH_{soln} \approx 0\)), and the entropic factor due to the increase in disorder is dominant (Figure \(\PageIndex{4}\)). Consequently, all gases dissolve readily in one another in all proportions to form solutions.

Figure \(\PageIndex{4}\): Formation of a Solution of Two Gases. (top) Pure samples of two different gases are in separate bulbs. (bottom) When the connecting stopcock is opened, diffusion causes the two gases to mix together and form a solution. Even though \(ΔH_{soln}\) is zero for the process, the increased entropy of the solution (the increased disorder) versus that of the separate gases favors solution formation.

Example \(\PageIndex{1}\)

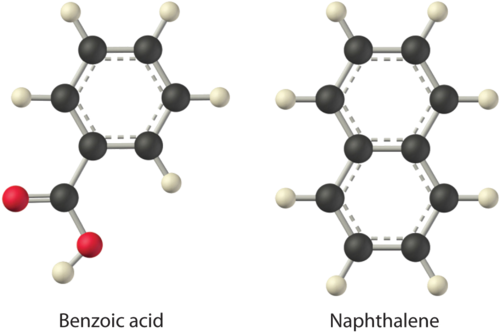
Considering \(\ce{LiCl}\), benzoic acid (\(\ce{C6H5CO2H}\)), and naphthalene, which will be most soluble and which will be least soluble in water?

Given: three compounds

Asked for: relative solubilities in water

Strategy: Assess the relative magnitude of the enthalpy change for each step in the process shown in Figure \(\PageIndex{2}\). Then use Table \(\PageIndex{2}\) to predict the solubility of each compound in water and arrange them in order of decreasing solubility.

Solution:

The first substance, \(\ce{LiCl}\), is an ionic compound, so a great deal of energy is required to separate its anions and cations and overcome the lattice energy (ΔH₂ is far greater than zero in Equation \(\ref{13.1.1}\)). Because water is a polar substance, the interactions between both Li⁺ and Cl⁻ ions and water should be favorable and strong. Thus we expect \(ΔH_3\) to be far less than zero, making LiCl soluble in water. In contrast, naphthalene is a nonpolar compound, with only London dispersion forces holding the molecules together in the solid state. We therefore expect \(ΔH_2\) to be small and positive. We also expect the interaction between polar water molecules and nonpolar naphthalene molecules to be weak \(ΔH_3 \approx 0\). Hence we do not expect naphthalene to be very soluble in water, if at all. Benzoic acid has a polar carboxylic acid group and a nonpolar aromatic ring. We therefore expect that the energy required to separate solute molecules (ΔH₂) will be greater than for naphthalene and less than for LiCl. The strength of the interaction of benzoic acid with water should also be intermediate between those of LiCl and naphthalene. Hence benzoic acid is expected to be more soluble in water than naphthalene but less soluble than \(\ce{LiCl}\). We thus predict \(\ce{LiCl}\) to be the most soluble in water and naphthalene to be the least soluble.

Exercise \(\PageIndex{1}\)

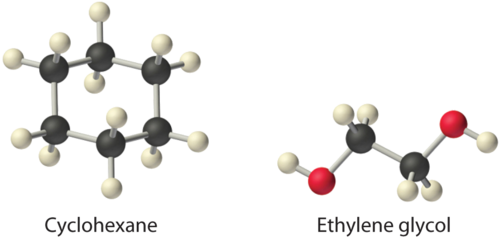
Considering ammonium chloride, cyclohexane, and ethylene glycol (\(HOCH_2CH_2OH\)), which will be most soluble and which will be least soluble in benzene?

Answer

The most soluble is cyclohexane; the least soluble is ammonium chloride.

Summary

Solutions are homogeneous mixtures of two or more substances whose components are uniformly distributed on a microscopic scale. The component present in the greatest amount is the solvent, and the components present in lesser amounts are the solute(s). The formation of a solution from a solute and a solvent is a physical process, not a chemical one. Substances that are miscible, such as gases, form a single phase in all proportions when mixed. Substances that form separate phases are immiscible. Solvation is the process in which solute particles are surrounded by solvent molecules. When the solvent is water, the process is called hydration. The overall enthalpy change that accompanies the formation of a solution, \(ΔH_{soln}\), is the sum of the enthalpy change for breaking the intermolecular interactions in both the solvent and the solute and the enthalpy change for the formation of new solute–solvent interactions. Exothermic (\(ΔH_{soln} < 0\)) processes favor solution formation. In addition, the change in entropy, the degree of disorder of the system, must be considered when predicting whether a solution will form. An increase in entropy (a decrease in order) favors dissolution.