6.11: Standard Temperature and Pressure
- Page ID
- 213228
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- State the value of standard temperature for Gas Law experiments.
- State the value of standard pressure for Gas Law experiments.
- Apply an STP conversion factor to convert between a molar quantity of a gas and its corresponding volume.
- Apply multiple conversion factors to solve problems that involve complex molar relationships.
As stated in Section 6.3, the original Gas Law experiments were limited to the investigation of two of the four measurable properties of gases. The measurements that were associated with two variables were held constant, so that any experimental change in the third quantity could only influence the value of the fourth. The subsequent sections presented and applied the Gas Laws, which relate the quantities that are altered in a particular trial. However, in order for any collected data to be meaningful, the experiment that was performed must be reproducible. Therefore, in order to complete every experimental trial under the same conditions, scientists were required to standardize the values of the two variables that were held constant.
Standard Temperature and Pressure (STP)
Recall that Avogadro's Law directly relates an amount of gas to its volume under isothermal and isobarometric conditions. As described previously, the temperature and pressure of a gas impact the behaviors of its constituent particles, which, in turn, influence the volume of the gas. The application of pressure causes gaseous particles to move closer to one another, which decreases the overall volume of the gas. Additionally, by decreasing the temperature of a gas, its constituent particles move more slowly and, therefore, collide less often with the surfaces of the container in which they are held, which causes the container to shrink. Since the pressure and temperature at which a gas are held directly influence the volumetric results of an Avogadro's Law experiment, scientists who completed trials using different "constant" conditions generated inconsistent data and, therefore, were unable to corroborate the experimental findings of their peers. In order to eliminate these variations, scientists chose to perform all Avogadro's Law experiments at a temperature of 273 Kelvin and under 1 atmosphere of pressure.
Under these conditions, which became known as standard temperature and pressure (STP), scientists discovered that 1 mole of a gas, regardless of its identity, occupied a volume of 22.4 liters. Recall that the value of the constant, k4, that is associated with the Avogadro's Law equation typically varies based on the identity of the gas that is being investigated. Therefore, since the amount of space that is occupied by a gas is independent of the identity of that gas at STP, the volumetric value that is given above is a chemically-significant quantity and, therefore, is defined as a molar standard.
Equality Pattern
Every molar standard has a corresponding equality pattern, which contains one number and two units on both sides of an equal sign. The left side of the STP equality pattern that is shown below contains a numerical value of "1," which is associated with the unit "mol." The right side of this equality pattern, which utilizes the volumetric value, "22.4," as its numerical quantity, has a primary unit of "L." The secondary unit positions, which are indicated as "blanks" in the equality pattern that is shown below, should be occupied by units that are relevant to the identity of the specific chemical that is referenced in a given problem. In particular, the chemical formula of the gas that is being considered should be inserted into both of these positions. A chemical name should not be used in this, or any, equality, and the relative order of the two units on either side of an STP equality should not be interchanged.
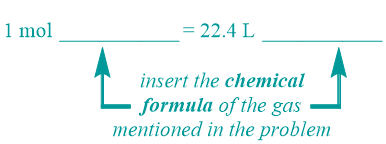
Indicator Phrase
Recall that all molar standards have a corresponding indicator word or phrase that identifies which relationship and, therefore, which equality pattern, must be applied to solve the problem at-hand. Because the volumetric value that is associated with this equality is only valid at an experimental temperature of 273 Kelvin and under 1 atmosphere of pressure, the phrase "at STP" must be present to indicate that an STP equality should be used to solve the given problem.
Calculations
For example, calculate how many moles of molecular chlorine gas are present in 75.0 liters of molecular chlorine at STP.
The phrase "at STP" indicates that the chemical formula for the gas that is referenced in the problem, molecular chlorine, Cl2, should be incorporated into both of the secondary unit positions in the STP equality pattern that was developed above. The resultant equality, 1 mol Cl2 = 22.4 L Cl2, must then be applied as a conversion factor to eliminate the given unit, "liters of molecular chlorine." Applying the correct number of significant figures to the calculated quantity results in the final answer that is shown below.
\( {\text {75.0}}\) \({\cancel{\rm{L} \; \rm{Cl_2}}} \times\) \( \dfrac{1 \; \rm{mol} \; \rm{Cl_2}}{22.4 \; \cancel{\rm{L} \; \rm{Cl_2}}}\) = \( {\text {3.348214...}}\) \({\rm{mol} \; \rm{Cl_2}}\) ≈ \( {\text {3.35}}\) \({\rm{mol} \; \rm{Cl_2}}\)
Consider the following balanced chemical equation.
\(\ce{CaCN_2} \left( s \right) + \) \(3 \; \ce{H_2O} \left( l \right) \rightarrow\) \(\ce{CaCO_3} \left( s \right) + \) \(2 \; \ce{NH_3} \left( g \right)\)
Calculate how many milliliters of nitrogen trihydride gas are generated if 0.17 moles of calcium cyanamide, CaCN2, are consumed in this reaction at STP.
Solution
Indicator Information & Equality Patterns
Because both of the chemicals that are referenced in the problem, nitrogen trihydride, NH3, and calcium cyanamide, CaCN2, are also present in the given reaction equation, a stoichiometric equality should be developed and applied to solve this problem. The chemical formulas for nitrogen trihydride, NH3, and calcium cyanamide, CaCN2, are incorporated into the secondary unit positions on the left and rightsides, respectively, of this equality. Since the coefficient that is associated with nitrogen trihydride, NH3, is a "2" in the given chemical equation, a 2 is inserted into the numerical position on the left side of this equality. Finally, because the coefficient that corresponds to calcium cyanamide, CaCN2, is an unwritten "1" in the balanced chemical equation, a 1 is inserted into the numerical position on the right side of this equality, as shown below.
2 mol NH3 = 1 mol CaCN2
Additionally, the phrase "at STP" indicates that an STP equality should also be developed and applied to solve this problem. The chemical formula for the gas that is referenced in the problem, nitrogen trihydride, NH3, should be incorporated into both of the secondary unit positions in this equality, as shown below.
1 mol NH3 = 22.4 L NH3
Dimensional Analysis
In order to completely eliminate the given unit, "moles of calcium cyanamide," a conversion factor based on the stoichiometric equality must be applied first. However, the unit that results upon the cancelation of "moles of calcium cyanamide" is "mol NH3," which is not the desired final unit. Therefore, a second conversion factor, based on the STP equality, must be applied.
The unit that results upon the cancelation of the intermediate unit "mol NH3" is "L NH3," which still is not the desired final unit. In order to convert the intermediate unit "L NH3" to the desired final unit, "milliliters of nitrogen trihydride," a prefix modifier equality that relates these two units must be developed and applied. As discussed in Section 1.8, a unit that contains a prefix modifier, such as "milliliters," can be related back to its base unit, "liters," by replacing the prefix modifier, "milli" (m), with its meaning, "10-3," as shown below.
mL = 10-3 L
While not absolutely necessary, a prefix modifier equality can be simplified by rewriting the numerical quantity as a decimal, which can then be eliminated by dividing both sides of the equality by 0.001, resulting in the relationship that is shown below.
mL = 0.001 L
1,000 mL = L
Before applying one of these relationships to cancel the the intermediate unit "L NH3," the chemical formula for nitrogen trihydride, NH3, must be added as a secondary unit on each side of the equal sign. After incorporating this chemical formula, any of these equalities can be applied to completely cancel the intermediate unit "L NH3," as shown below.
\( {\text {0.17}} {\cancel{\rm{mol} \; \rm{CaCN_2}}} \times\) \( \dfrac{2 \; \bcancel{\rm{mol} \; \rm{NH_3}}}{1 \; \cancel{\rm{mol} \; \rm{CaCN_2}}}\) × \( \dfrac{22.4 \; \cancel{\rm{L} \; \rm{NH_3}}}{1 \; \bcancel{\rm{mol} \; \rm{NH_3}}}\) × \( \dfrac{1,000 \; \rm{mL} \; \rm{NH_3}}{\cancel{\rm{L} \; \rm{NH_3}}}\) = \( {\text {7,616}}\) \({\rm{mL} \; \rm{NH_3}}\)
≈ \( {\text {7,600}}\) \({\rm{mL} \; \rm{NH_3}}\)
The solution is calculated by multiplying the given number by the value in each numerator, and then dividing by the quantity in each denominator. When using a calculator, each conversion factor should be entered in parentheses, or the "=" key should be used after each division. Applying the correct number of significant figures to the calculated quantity results in the final answer that is shown above.
Consider the following chemical equation.
___ \( \ce{S} \left( s \right) + \) ___ \( \ce{O_2} \left( g \right) + \) ___ \(\ce{H_2O} \left( l \right) \rightarrow\) ___ \( \ce{H_2SO_4} \left( aq \right)\)
- Balance this equation by writing coefficients in the "blanks," as necessary.
- Classify this reaction as a combination, a decomposition, a single replacement, a double replacement, or a combustion reaction.
- Identify the state of matter in which sulfur participates in this reaction.
- Calculate the molecular weight of sulfuric acid, H2SO4. Represent the resultant solution as a molar equality and as a "hidden" conversion factor.
- Calculate how many liters of molecular oxygen gas must be consumed if 76.2 grams of sulfuric acid, H2SO4, are generated in this reaction at STP.
- Answer a
- In order to balance a chemical equation, the quantities of each type of element and polyatomic ion that are present in the reactants and the products of the reaction must be determined. The product of this reaction contains hydrogen, H, and the sulfate ion, SO4-2, which is a polyatomic anion. However, because the sulfate ion is not present on the reactant side of the arrow, this ion cannot be balanced as a single entity and, therefore, must be divided into its constituent elements, sulfur, S, and oxygen, O. The quantities in which these elements are present in the given reaction equation are summarized in the table that is shown below. Note that oxygen, O, is present in two of the reactants that are shown in this equation. Therefore, in order to determine the number of oxygens that are present on the reactant side of this equation, the subscripts on both oxygens must be added.
Element or Ion Reactants Products Balanced S 1 1 
O 3 4 
H 2 2 
Since both sides of the equation contain equal amounts of sulfur, S, and hydrogen, H, those elements are balanced. Oyxgen, O, is not balanced, because this element is present in different quantities on the reactant and product sides of the reaction arrow. Therefore, one or more coefficients must be written in the "blanks" above, in order to balance this reaction.
In order to balance oxygen, O, a coefficient should be written in one of the "blanks" on the left side of the equation, as fewer oxygens are present on this side of the reaction arrow. However, as stated above, oxygen, O, is present in two of the reactants, molecular oxygen, O2, and water, H2O, in this equation. Because water, H2O, also contains hydrogen, H, which is already balanced, a coefficient should not be placed in the "blank" that is associated with this molecule. Instead, a coefficient should be written in the "blank" that corresponds to molecular oxygen, O2. The value of this coefficient, 1.5, is determined by first subtracting 1 from the larger quantity of this element, 4, in order to account for the oxygen, O, that is present in water, H2O, and then dividing the resultant quantity, 3, by the count of this element, 2, that is associated with molecular oxygen, O2, on the left side of the equation. Inserting this coefficient results in the chemical equation that is shown below.___ \( \ce{S} \left( s \right) + \) 1.5 \( \ce{O_2} \left( g \right) + \) ___ \(\ce{H_2O} \left( l \right) \rightarrow\) ___ \( \ce{H_2SO_4} \left( aq \right)\)
As oxygen, O, is the only element that is present in this chemical formula, incorporating this coefficient does not alter the amounts of sulfur, S, or hydrogen, H, that are present on the reactant side of the equation. The updated quantity of this element is reflected in the table that is shown below. Because oxygen is present in both of the reactants, the quantities of oxygen in both of these molecules must be added to determine the amount of oxygen that is present on the reactant side of this equation. Inserting this coefficient balances oxygen, O, as intended. Therefore, all of the components of this equation are now balanced.
Element or Ion Reactants Products Balanced S 1 1 
O \( \cancel{\rm{3}}\) 4 4 
H 2 2 
However, a fractional coefficient, 1.5, is written in the equation that is shown above. As a result, all of the coefficients in this equation, including the unwritten "1"s that are understood to occupy the first, third, and fourth blanks, must be multiplied by 2, in order to cancel this half-fraction. The doubled coefficient values are reflected in the chemical equation that is shown below.2 \( \ce{S} \left( s \right) + \) 3 \( \ce{O_2} \left( g \right) + \) 2 \(\ce{H_2O} \left( l \right) \rightarrow\) 2 \( \ce{H_2SO_4} \left( aq \right)\)
By multiplying all of the coefficients in this equation by 2, the quantities in which sulfur, S, oxygen, O, and hydrogen, H, are present in the equation have changed, as shown in the table below, but their relative ratios have not. Therefore, all of the components of this equation are still balanced.
Element or Ion Reactants Products Balanced S \( \bcancel{\rm{1} } \) 2 \( \bcancel{\rm{1} } \) 2 
O \( \cancel{\rm{3}}\) \( \bcancel{\rm{4} } \) 8 \( \bcancel{\rm{4} } \) 8 
H \( \bcancel{\rm{2} } \) 4 \( \bcancel{\rm{2} } \) 4 
Finally, these coefficients cannot be divided, as they do not all share a common divisor that would result in the calculation of four whole number coefficients. Therefore, the final equation that is presented above is chemically-correct, as written. - Answer b
- This reaction is classified as a combination because only a single molecule, sulfuric acid, H2SO4, is present on the right side of the reaction arrow.
- Answer c
- Sulfur, S, participates in this reaction as a solid, as indicated by the "\( \left( s \right)\)" that is associated with its formula in the given chemical equation.
- Answer d
- In order to calculate the molecular weight of a compound, the mass contribution of each element that is found within that compound must first be determined. Because sulfuric acid, H2SO4, contains three elements, the mass contributions of hydrogen, H, sulfur, S, and oxygen, O, must be calculated. In a mass contribution calculation,
- the chemical formula of the element that is being considered is written as the secondary unit for all numerical quantities;
- the subscript for the element that is being considered is inserted into the "component within" portion of the mass contribution pattern;
- the atomic mass average of the element that is being considered is recorded to the hundredths place in the numerator of the atomic weight conversion factor; and
- each resultant calculated value is reported to the hundredths place.
\( {\text {2}}\) \({\cancel{\rm{mol} \; \rm{H}}}\) × \( \dfrac{1.01 \; \rm{g} \; \rm{H}}{1\; \cancel{\rm{mol} \; \rm{H}}}\) = \( {\text {2.02}}\) \({\rm{g} \; \rm{H}}\)
\( {\text {1}}\) \({\cancel{\rm{mol} \; \rm{S}}}\) × \( \dfrac{32.07 \; \rm{g} \; \rm{S}}{1\; \cancel{\rm{mol} \; \rm{S}}}\) = \( {\text {32.07}}\) \({\rm{g} \; \rm{S}}\)
\( {\text {4}}\) \({\cancel{\rm{mol} \; \rm{O}}}\) × \( \dfrac{16.00 \; \rm{g} \; \rm{O}}{1\; \cancel{\rm{mol} \; \rm{O}}}\) = \( {\text {64.00}}\) \({\rm{g} \; \rm{O}}\)
The numerical value of the molecular weight of sulfuric acid, H2SO4, 98.09, is determined by adding the mass contributions that are shown above and should be reported to the hundredths place.
In order to develop a molecular weight equality, the calculated molecular weight of the compound is equated to 1 mol of the compound, and the chemical formula of the entire compound is utilized as the secondary unit on both sides of the resultant equality, as shown below.1 mol H2SO4 = 98.09 g H2SO4
Finally, this equality can be rewritten as a "hidden" conversion factor by dividing the quantity on the right side of the equal sign by the information on the left side, removing the "1," and condensing the primary unit to "g/mol." The chemical formula of the entire compound is still utilized as the secondary unit in this representation of molecular weight, as shown below.
98.09 g/mol H2SO4
- Answer e
- Indicator Information & Equality Patterns
The mass unit "grams" indicates that a mass-based equality should be developed and applied to solve this problem. As multiple chemicals are referenced in this problem, the chemical formula for the substance that is written in closest physical proximity to the indicator word "grams," "sulfuric acid," H2SO4, is incorporated into the mass-based equality. Since sulfuric acid, H2SO4, is a compound, a molecular weight equality for this chemical, which was developed in Part (d) and is replicated below, should be applied to solve this problem.1 mol H2SO4 = 98.09 g H2SO4
Additionally, because both of the chemicals that are referenced in the problem, molecular oxygen, O2, and sulfuric acid, H2SO4, are also present in the given reaction equation, a stoichiometric equality should also be developed and applied to solve this problem. The chemical formulas for molecular oxygen, O2, and sulfuric acid, H2SO4, are incorporated into the secondary unit positions on the left and right sides, respectively, of this equality. Since the coefficient that is associated with molecular oxygen, O2, is a "3" in the chemical equation that was balanced in Part (a), a 3 is inserted into the numerical position on the left side of this equality. Finally, because the coefficient that corresponds to sulfuric acid, H2SO4, is a "2" in the balanced chemical equation, a 2 is inserted into the numerical position on the right side of this equality, as shown below.3 mol O2 = 2 mol H2SO4
Finally, the phrase "at STP" indicates that an STP equality should also be developed and applied to solve this problem. The chemical formula for the gas that is referenced in the problem, molecular oxygen, O2, should be incorporated into both of the secondary unit positions in this equality, as shown below.1 mol O2 = 22.4 L O2
Dimensional Analysis
In order to completely eliminate the given unit, "grams of sulfuric acid," a conversion factor based on the molecular weight equality must be applied first. However, the unit that results upon the cancelation of "grams of sulfuric acid" is "mol H2SO4," which is not the desired final unit. Therefore, a second conversion factor, based on the stoichiometric equality, must be applied. The unit that results upon the cancelation of the intermediate unit "mol H2SO4" is "mol O2," which still is not the desired final unit. Therefore, the STP equality must be applied as a third conversion factor, as shown below.\( {\text {76.2}}\) \({\cancel{\rm{g} \; \rm{H_2SO_4}}} \times\) \( \dfrac{1 \; \bcancel{\rm{mol} \; \rm{H_2SO_4}}}{98.09 \; \cancel{\rm{g} \; \rm{H_2SO_4}}}\) × \( \dfrac{3 \; \cancel{\rm{mol} \; \rm{O_2}}}{2 \; \bcancel{\rm{mol} \; \rm{H_2SO_4}}}\) × \( \dfrac{22.4 \; \rm{L} \; \rm{O_2}}{1 \; \cancel{\rm{mol} \; \rm{O_2}}}\) = \( {\text {26.101743...}}\) \({\rm{L} \; \rm{O_2}}\) ≈ \( {\text {26.1}}\) \({\rm{L} \; \rm{O_2}}\)
The solution is calculated by multiplying the given number by the value in each numerator, and then dividing by the quantity in each denominator. When using a calculator, each conversion factor should be entered in parentheses, or the "=" key should be used after each division. Applying the correct number of significant figures to the calculated quantity results in the final answer that is shown above.

