2.5: Locating Electrons: Orbitals and Electron Configurations
- Page ID
- 213213
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Define energy level.
- Define orbital.
Electrons were defined and described in an earlier section of this chapter. As previously stated, scientists initially believed that electrons were tiny particles that were randomly-dispersed across a considerable volume, just as raindrops are little bits of water that are scattered throughout rain clouds. However, this concept of an "electron cloud" was proven to be inaccurate by a Danish physicist named Niels Bohr.
Energy Levels
In 1913, Bohr realized that electrons had defined, or quantized, energies that could only be possible if electrons were located at specific distances from the nucleus, much like a ladder only has rungs at certain heights. The specific distances from the nucleus at which electrons are located became known as energy levels. Every period on the periodic table has a corresponding energy level; therefore, a total of seven energy levels exist in every atom.

Orbitals
The locations of electrons can be specified to an even greater level of accuracy. Every energy level is associated with one or more orbitals, which are regions in space in which an electron can be found. Four different types of orbitals, called s orbitals, p orbitals, d orbitals, and f orbitals, exist. Only s orbitals and p orbitals will be discussed further, as understanding d orbitals and f orbitals will not be necessary for the applications that will be presented in this text.
s Orbitals
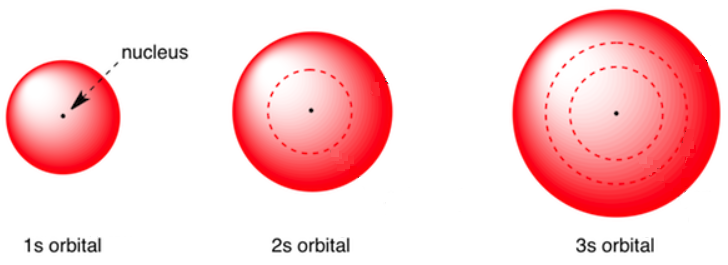
s orbitals are spherical in shape, making them perfectly symmetrical, and are centered around the nucleus of an atom. Each of the seven energy levels has its own s orbital. Figure \(\PageIndex{2}\) shows the s orbitals for the first three energy levels. Note that the size of the orbital is proportional to the value of the energy level. In other words, smaller orbitals are associated with lower energy levels, and the orbitals for higher energy levels are larger. Finally, the 1s orbital is able to fit completely inside of the 2s orbital, which, in turn, is completely contained within the 3s orbital. This "nesting" effect can be likened to the appearance of Russian "stacking dolls," which are a set of seven wooden dolls of decreasing sizes that all fit inside of one another.

p Orbitals
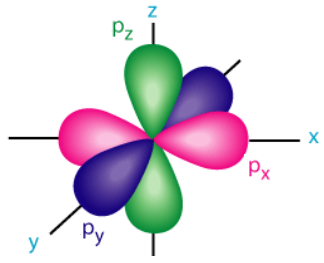
p orbitals are described as "dumbbell"-shaped and are still centered around the nucleus of an atom. Since a p orbital is not perfectly symmetrical, it must also have a defined orientation. Specifically, a p orbital can align with the x-, y-, or z-axis in three-dimensional space. While the first energy level does not have any corresponding p orbitals, each of the remaining energy levels do. Furthermore, all three of the aforementioned p orbital orientations exist for each of these energy levels. These three orientations, which are called px, py, and pz orbitals, respectively, superimpose to create the "flower" shape that is shown below in Figure \(\PageIndex{4}\). Finally, much like s orbitals, p orbitals also "nest" and become larger in size as the value of their energy level increases.
Electron Maximums
Finally, Bohr determined that every orbital could contain a maximum of two electrons. Since only one s orbital orientation exists, every energy level can hold a maximum of two electrons in s orbitals. However, three unique p orbital orientations (px, py, and pz) exist, beginning at the second energy level. Since each of these p orbitals can contain a maximum of two electrons, every corresponding energy level can hold a maximum of six electrons in its combined p orbitals.
Electron Configurations
The energy level, orbital, and electron maximum information described above can be summarized in an electron configuration. This notation allows chemists to explicitly state the location of each individual electron within an atom. In particular, the combination of an energy level value and an orbital type denote the location of the electron of interest, and a superscript indicates the maximum number of electrons that can be collectively-contained in that orbital or orbital set. The electron configuration for the first six orbitals/orbital sets that exist for an atom is shown below.
1s22s22p63s23p64s2
Note that the location of up to 20 electrons (2+2+6+2+6+2) can be specified using these six orbitals/orbital sets. As the periodic table currently contains 118 elements, this electron configuration pattern can be greatly expanded-upon, in order to account for any additional electrons. However, the partial configuration shown above is sufficient for the applications that will be presented in the next sections of this text.

