2.4: Neutrons: Isotopes and Mass Number Calculations
- Page ID
- 214181
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Describe the location, charge, and relative mass of the neutron.
- Define isotope and mass number.
- Determine the number of protons, neutrons, and electrons in a specific isotope of an element.
- Represent a single isotope of an element using the three main elemental symbolisms.
The final subatomic particle was not discovered until 1932. In order to account for the neutral charge of an atom as a whole, the number of positively-charged protons and negatively-charged electrons found within an atom must be equal. Therefore, any remaining subatomic particles must be uncharged, so as to not upset this established charge balance. Indeed, neutrons, which were named as a result of their neutral charge, do not possess any electrical properties. Consequently, these subatomic particles, which are symbolized using the notation "n0," were incredibly difficult to detect. Neutrons are also located in the nucleus of an atom, and the mass of a neutron was found to be just slightly greater than the mass of a proton.
Each subatomic particle exists to serve a specific purpose. As stated in the previous section, the number of valence electrons present in an atom dictates the reactivity of that element. The number of protons found within an atom defines the identity of that atom, and all of an atom's protons collectively attract the surrounding electrons, keeping the latter bound to the atom. Recall, however, that all protons, which each bear a +1 charge, are densely-packed into the central region of an atom. Therefore, each positively-charged proton must be strongly repelled by every other proton in the nucleus, and, furthermore, the combined strength of these repulsive forces is substantial enough to splinter the nucleus. However, neutrons effectively act as "nuclear glue" and allow the protons to exist in close physical proximity to one another. In other words, neutrons are the subatomic particle responsible for maintaining the structural integrity of the nucleus.
Finally, recall that every atom of a certain element must have a defined number of protons and electrons. Every atom of carbon, C, that exists in the known universe is defined to contain 6 protons, because its atomic number is 6, and must also contain 6 electrons, in order for the atom to maintain an overall net neutral charge. However, the number of neutrons within an atom of an element is not defined by the atomic number of that element. In fact, the number of neutrons present in an element can vary from atom to atom. The "glue" analogy found within the previous paragraph can be extended to explain this phenomenon. While a minimum amount of glue is required to adhere one object to another, a small amount of excess glue will not prevent those objects from sticking together, but a large excess of glue could prove to be problematic. Likewise, each element must contain a minimum number of neutrons to hold the nucleus together, but could contain a small number of additional neutrons without sacrificing the structural integrity of the nucleus. However, a nucleus that contains too many neutrons will become unstable and undergo radioactive decay, which will be discussed in Chapter 9 of this text.
Mass Number
The mass number of an atom is equal to the total number of protons and neutrons contained in its nucleus. This definition can be represented in an equation, as shown below.
Mass Number = # of Protons + # of Neutrons
The true mass of an atom is an incredibly small quantity. To simplify the numerical values being used, the mass of a single proton is assigned a value of 1 atomic mass unit, or amu. As the mass of a neutron is approximately the same as the mass of a proton, each neutron that is present is also given a value of 1 amu. Since the mass of an electron is 1/2,000th of the mass of a proton, any contribution that electrons make to the overall mass of an atom is negligible. Therefore, the number of electrons present in an atom are ignored when calculating the mass number of that atom.
Use a periodic table to calculate the mass number of a hydrogen atom that contains 2 neutrons.
Solution
The mass number of an atom is calculated by adding together the number of protons and neutrons that are found within that atom. The number of neutrons is given, but the number of protons must be determined from the atomic number for the element. In this case, hydrogen (H) has an atomic number of 1 and, therefore, every atom of hydrogen will contain 1 proton. The equation shown above can then be applied, as follows.
Mass Number = # of Protons + # of Neutrons
Mass Number = 1 + 2
Therefore, this particular atom of hydrogen will have a mass number of 3.
Note that the mass number calculated in Example \(\PageIndex{1}\) does not match the number underneath the elemental symbol and name for hydrogen on the periodic table. This discrepancy can be explained by a subtle, but incredibly important, piece of information: The calculation performed in Example \(\PageIndex{1}\) was done for a single atom of hydrogen. However, the periodic table is intended to represent all of the atoms of hydrogen in the known universe. Since every existing atom of hydrogen must contain 1 proton, the atomic number that is written above hydrogen's elemental symbol truly does represent every atom of hydrogen.
However, recall that the number of neutrons contained in an element can vary from atom to atom. Changing the number of neutrons present in an atom will, in turn, cause these individual atoms of hydrogen to have different calculated mass numbers. These individual "versions" of an element are called isotopes, which are defined as atoms of an element that have the same atomic numbers and, therefore, contain the same number of protons, but different mass numbers, and, therefore, contain differing numbers of neutrons. Three isotopes of hydrogen are modeled in Figure \(\PageIndex{1}\). Most hydrogen atoms have one proton, one electron, and do not contain any neutrons, but less common isotopes of hydrogen can contain either one or two neutrons. Hydrogen is unique, in that its isotopes are given special names, which are also shown below in Figure \(\PageIndex{1}\).

For spatial reasons, listing the mass numbers for all of an element's isotopes within a single box on the periodic table is impractical. Instead, a weighted average, called an atomic mass average, is calculated. A weighted average takes into account not only the mass number of each isotope, but also how prevalent, or common, that isotope is in nature, relative to each of that element's other isotopes. Therefore, an atomic mass average is a quantity that truly represents all isotopes of a given element, making it appropriate for inclusion on the periodic table.
Use a periodic table to determine the following information for an atom that has an atomic number of 74 and a mass number of 186.
- Elemental symbol
- Elemental name
- Number of protons contained in the atom
- Number of electrons contained in the atom
- Number of neutrons contained in the atom
Solutions
- The atomic number of an element is found above the elemental symbol within a box on the periodic table. The element with an atomic number of 74 is symbolized as W.
- The element with an atomic number of 74 is named tungsten.
- The number of protons present in an atom is defined by the element's atomic number. Therefore, every atom of tungsten contains 74 protons.
- Since an atom must have an overall neutral charge, the number of protons and electrons found within an atom of an element must be equal. Therefore, every atom of tungsten also contains 74 electrons.
- The mass number of an atom is calculated by adding together the number of protons and neutrons that are found within that atom, as shown below.
Mass Number = # of Protons + # of Neutrons
Since the mass number was provided, this equation can be rearranged to determine the number of neutrons contained in this specific isotope of tungsten.
186 = 74 + # of Neutrons
186 - 74 = # of NeutronsTherefore, this particular atom of tungsten contains 112 neutrons.
Elemental Symbolisms
In total, 252 stable isotopes have been isolated for 80 different elements. Factoring in the number of unstable isotopes that have been observed causes the total number of known elemental isotopes to increase substantially. While each of hydrogen's three most common isotopes has a unique name, it would ultimately be highly impractical to establish different names for every isotope of every element that has been shown to exist. Therefore, scientists utilize three different elemental symbolisms to refer to specific elemental isotopes. The first two symbolisms are very similar, in that each includes the elemental name, or elemental symbol, of an element, followed by a dash and a numerical value, which corresponds to the mass number of a particular isotope of that element. In the third type of elemental symbolism, which is called a nuclear symbol, the mass number of the isotope is positioned as a superscript before an elemental symbol, and the atomic number of the element is written directly underneath the mass number. It is important to note the difference between an isotope and an elemental symbolism. Figure \(\PageIndex{2}\) models these three different elemental symbolisms, which all represent the same isotope, since each has an identical mass number.
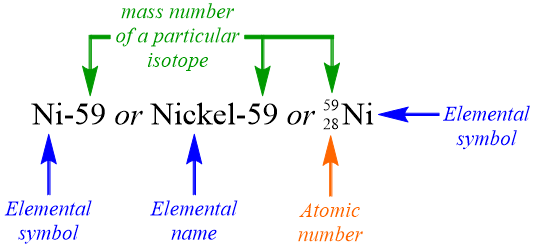
Write the nuclear symbol of the isotope that is described in Example \(\PageIndex{2}\).
Solutions
In a nuclear symbol, the mass number of the isotope is positioned as a superscript before an elemental symbol, and the atomic number of the element is written directly underneath the mass number.
The isotope in Example \(\PageIndex{2}\) has an atomic number of 74, a mass number of 186, and is symbolized as W. When this information is incorporated into this notation, the nuclear symbol shown below results.
\(\ce{^{186}_{74}W}\)
Determine how many protons, electrons, and neutrons are present in an atom of each of the following isotopes.
- \(^{40}_{19}\ce{K}\)
- Zinc-65
Solutions
- This isotope is symbolized using a nuclear symbol. In this notation, the atomic number of the isotope is written as a subscript. Since the atomic number indicates both the number of protons and the number of electrons present in an atom, this isotope contains 19 protons and 19 electrons. The number of neutrons in the isotope can be calculated from its mass number, which is written as a superscript in a nuclear symbol.
Mass Number = # of Protons + # of Neutrons
40 = 19 + # of Neutrons
40 - 19 = # of NeutronsTherefore, there are 21 neutrons in this isotope of potassium (K).
- This isotope is represented using the second symbolism shown in Figure \(\PageIndex{2}\). When using this notation, the name of the element must be used to find its atomic number. Since zinc (Zn) has an atomic number of 30, this isotope contains 30 protons and 30 electrons. The number of neutrons in the isotope can again be calculated from its mass number, which is the numerical value written after the dash in both representations shown in Figure \(\PageIndex{2}\).
Mass Number = # of Protons + # of Neutrons
65 = 30 + # of Neutrons
65 - 30 = # of NeutronsTherefore, there are 35 neutrons in this isotope of zinc (Zn).
Determine how many protons, electrons, and neutrons are present in an atom of each of the following isotopes.
- \(^{60}_{27}\ce{Co}\)
- Uranium-238
- Na-25
- Answer a
- This isotope is represented using a nuclear symbol. In this notation, the atomic number of the isotope is written as a subscript. Since the atomic number indicates both the number of protons and the number of electrons present in an atom, this isotope contains 27 protons and 27 electrons. The number of neutrons in the isotope can be calculated from its mass number, which is written as a superscript in a nuclear symbol.
Mass Number = # of Protons + # of Neutrons
Therefore, there are 33 neutrons in this isotope of cobalt (Co).
60 = 27 + # of Neutrons
60 - 27 = # of Neutrons - Answer b
- This isotope is represented using the second symbolism shown in Figure \(\PageIndex{2}\). When using this notation, the name of the element must be used to find its atomic number. Since uranium (U) has an atomic number of 92, this isotope contains 92 protons and 92 electrons. The number of neutrons in the isotope can again be calculated from its mass number, which is the numerical value written after the dash in both representations shown in Figure \(\PageIndex{2}\).
Mass Number = # of Protons + # of Neutrons
Therefore, there are 146 neutrons in this isotope of uranium (U).
238 = 92 + # of Neutrons
238 - 92 = # of Neutrons - Answer c
- This isotope is represented using the first symbolism shown in Figure \(\PageIndex{2}\). When using this notation, the symbol of the element must be used to find its atomic number. Since sodium (Na) has an atomic number of 11, this isotope contains 11 protons and 11 electrons. The number of neutrons in the isotope can again be calculated from its mass number, which is the numerical value written after the dash in both representations shown in Figure \(\PageIndex{2}\).
Mass Number = # of Protons + # of Neutrons
Therefore, there are 14 neutrons in this isotope of sodium (Na).
25 = 11 + # of Neutrons
25 - 11 = # of Neutrons

