13.2: The Distribution of Molecular Speeds is Given by the Maxwell-Boltzmann Distribution
- Last updated
- Save as PDF
- Page ID
- 426492
The Boltzmann Distribution
If we were to plot the number of molecules whose velocities fall within a series of narrow ranges, we would obtain a slightly asymmetric curve known as a velocity distribution. The peak of this curve would correspond to the most probable velocity. This velocity distribution curve is known as the Maxwell-Boltzmann distribution, but is frequently referred to only by Boltzmann's name. The Maxwell-Boltzmann distribution law was first worked out around 1860 by the great Scottish physicist, James Clerk Maxwell (1831-1879), who is better known for discovering the laws of electromagnetic radiation. Later, the Austrian physicist Ludwig Boltzmann (1844-1906) put the relation on a sounder theoretical basis and simplified the mathematics somewhat. Boltzmann pioneered the application of statistics to the physics and thermodynamics of matter and was an ardent supporter of the atomic theory of matter at a time when it was still not accepted by many of his contemporaries.


In section 27.2 we saw that the distribution function for molecular speeds in the x direction is given by:
\[f(v_x) = \underbrace{\sqrt{ \dfrac{m}{2\pi k_BT} }}_{\text{normalization term}} \underbrace{\exp \left(\dfrac{-mv_x^2}{2k_BT} \right)}_{\text{exponential term}} \nonumber \]
However, real gas samples have molecules not only with a distribution of molecular speeds and but also a random distribution of directions. Using normal vector magnitude properties (or simply using the Pythagorean Theorem), it can be seen that
\[ \langle v \rangle^2 = \langle v_x \rangle^2 + \langle v_y \rangle^2 + \langle v_z \rangle^2 \nonumber \]
Since the direction of travel is random, the velocity can have any component in x, y, or z directions with equal probability. As such, the average value of the x, y, or z components of velocity should be the same. And so
\[ \langle v \rangle^2 = 3 \langle v_x \rangle^2 \nonumber \]
Substituting this into the expression for pressure yields
\[ p =\dfrac{ N_{tot}m}{3V} \langle v \rangle^2 \nonumber \]
All that remains is to determine the form of the distribution of velocity magnitudes the gas molecules can take. In his 1860 paper (Illustrations of the dynamical theory of gases. Part 1. On the motions and collisions of perfectly elastic spheres, 1860), Maxwell proposed a form for this distribution of speeds which proved to be consistent with observed properties of gases (such as their viscosities). He derived this expression based on a transformation of coordinate system from Cartesian coordinates (\(x\), \(y\), \(z\)) to spherical polar coordinates (\(v\), \(\theta\), \(\phi\)). In this new coordinate system, \(v\) represents the magnitude of the velocity (or the speed) and all of the directional data is carried in the angles \(\theta\) and \(\phi\). The infinitesimal volume unit becomes
\[ dx\,dy\,dz\, = v^2 \sin( \theta) \,dv\,d\theta \,d\phi \nonumber \]
Applying this transformation of coordinates Maxwell’s distribution took the following form
\[f(v) = 4\pi v^2 \left(\dfrac{m}{2\pi k_BT} \right)^{3/2} \exp \left(\dfrac{-mv^2}{2k_BT} \right) \label{27.3.1} \]
The Distribution of Speed over all Directions
The Distribution of Kinetic Energy in Three Dimensions
As noted above, the distribution function of molecular energies for one dimension is
\[f(v_x) = \sqrt{ \dfrac{m}{2\pi k_BT} } \exp \left(\dfrac{-mv_x^2}{2k_BT} \right) \nonumber \]
To obtain a three-dimensional probability distribution, you multiply the distribution function for each of the three dimensions so that
\[f(v_x, v_y, v_z) = \left(\dfrac{m}{2\pi k_BT} \right)^{3/2} \exp \left(\dfrac{-mv^2}{2k_BT} \right) \nonumber \]
given \[ \langle v \rangle^2 = \langle v_x \rangle^2 + \langle v_y \rangle^2 + \langle v_z \rangle^2 \nonumber \]
The Conversion of Energy Distribution to Speed Distribution
To convert the three-dimensional energy distribution to a speed distribution over all space, the energy distribution must be summed over all directions. This sum is usually described by imagining a "velocity space" in spherical polar coordinates. As noted above, in this new coordinate system, \(v\) represents the magnitude of the velocity (or the speed) and all of the directional data is carried in the angles \(\theta\) and \(\phi\). The infinitesimal volume unit becomes
\[ dx\,dy\,dz\, = v^2 \sin( \theta) \,dv\,d\theta \,d\phi \nonumber \]
You integrate over \(\theta\) and \(\phi\) to sum over all space, thus
\[f(v) = \left(\dfrac{m}{2\pi k_BT} \right)^{3/2} \exp \left(\dfrac{-mv^2}{2k_BT} \right) \underbrace {\int_0^{\pi} \int_0^{2\pi} v^2 \sin \theta d \phi d \theta}_{=4\pi v^2} \nonumber \]
This equation is rearranged to give
\[f(v) = 4\pi v^2 \left(\dfrac{m}{2\pi k_BT} \right)^{3/2} \exp \left(\dfrac{-mv^2}{2k_BT} \right) \nonumber \]
This function can be thought of as having three basic parts to it: a normalization constant (\(N\)), a velocity dependence (\(v^2\)), and an exponential term that contains the kinetic energy (\(½ mv^2\)).
Because the function represents the fraction of molecules with the speed \(v\), the sum of the fractions for all possible velocities must be unity. This sum can be calculated as an integral. The normalization constant ensures that
\[ \int_0^{\infty} f(v) dv = 1 \nonumber \]
Thus the normalization constant is
\[ N =4\pi \sqrt{\left( \dfrac{m}{2\pi k_BT} \right) ^3 } \nonumber \]
Velocity distributions depend on temperature and mass
Higher temperatures allow a larger fraction of molecules to acquire greater amounts of kinetic energy, causing the Boltzmann plots to spread out. Figure 27.3.2 shows how the Maxwell-Boltzmann distribution is affected by temperature. At lower temperatures, the molecules have less energy. Therefore, the speeds of the molecules are lower and the distribution has a smaller range. As the temperature of the molecules increases, the distribution flattens out. Because the molecules have greater energy at higher temperature, the molecules are moving faster.
Notice how the left ends of the plots are anchored at zero velocity (there will always be a few molecules that happen to be at rest.) As a consequence, the curves flatten out as the higher temperatures make additional higher-velocity states of motion more accessible. The area under each plot is the same for a constant number of molecules.
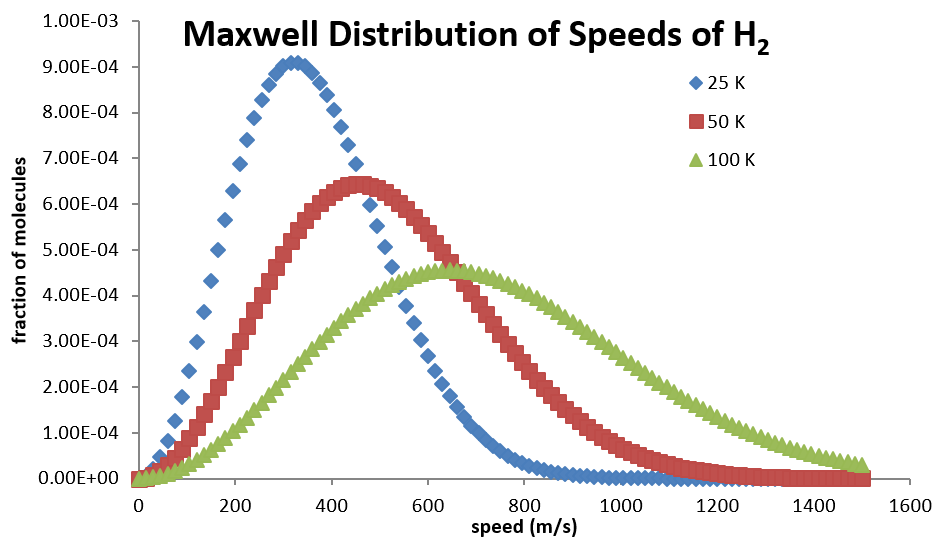
Calculating the Average Speed
Using the Maxwell distribution as a distribution of probabilities, the average molecular speed in a sample of gas molecules can be determined.
\[ \begin{align} \langle v \rangle & = \int _{-\infty}^{\infty} v \,f(v) dv \nonumber \\ & = \int _{-\infty}^{\infty} v\, 4\pi \sqrt{\left( \dfrac{m}{2\pi k_BT} \right) ^3 } v^2 \text{exp} \left( \dfrac{-m v^2}{2 k_BT} \right)\ dv \nonumber \\ & = 4\pi \sqrt{\left( \dfrac{m}{2\pi k_BT} \right) ^3 } \int _{-\infty}^{\infty} v^3 \text{exp} \left( \dfrac{-m v^2}{2 k_BT} \right)\ dv \nonumber \end{align} \nonumber \]
The following can be found in a table of integrals:
\[ \int_0^{\infty} x^{2n+1} e^{-ax^2} dx = \dfrac{n!}{2a^{n+1}} \nonumber \]
So
\[\langle v \rangle = 4\pi \sqrt{\left( \dfrac{m}{2\pi k_BT} \right) ^3 } \left[ \dfrac{1}{2 \left( \dfrac{m}{2 k_B T} \right) ^2 } \right] \nonumber \]
Which simplifies to
\[\langle v \rangle = \left( \dfrac{8 k_BT}{\pi m} \right) ^{1/2} \nonumber \]
Note: the value of \(\langle v \rangle \) is twice that of \(\langle v_x \rangle \) which was derived in an earlier example!
\[\langle v \rangle = 2\langle v_x \rangle \nonumber \]
Example 27.3.1 :
What is the average value of the squared speed according to the Maxwell distribution law?
Solution:
\[ \begin{align} \langle v^2 \rangle & = \int _{-\infty}^{\infty} v^2 \,f(v) dv \nonumber \\ & = \int _{-\infty}^{\infty} v^2\, 4\pi \sqrt{\left( \dfrac{m}{2\pi k_BT} \right) ^3 } v^2 \text{exp} \left( \dfrac{-m v^2}{2 k_BT} \right)\ dv \nonumber \\ & = 4\pi \sqrt{\left( \dfrac{m}{2\pi k_BT} \right) ^3 } \int _{-\infty}^{\infty} v^4 \text{exp} \left( \dfrac{-m v^2}{2 k_BT} \right)\ dv \nonumber \end{align} \nonumber \]
A table of integrals indicates that
\[ \int_0^{\infty} x^{2n} e^{-ax^2} dx = \dfrac{1 \cdot 3 \,cdot 5 \dots (2n-1)}{2^{n+1}a^n} \sqrt{\dfrac{\pi}{a}} \nonumber \]
Substitution (noting that \(n = 2\)) yields
\[\langle v^2 \rangle = 4\pi \sqrt{\left( \dfrac{m}{2\pi k_BT} \right) ^3 } \left[ \dfrac{1 \cdot 3}{2^3 \left( \dfrac{m}{2 k_BT} \right) ^2 } \sqrt{\dfrac{\pi}{\left( \dfrac{m}{2 k_BT} \right)}} \right] \nonumber \]
which simplifies to
\[\langle v^2 \rangle = \dfrac{3 k_BT}{ m} \nonumber \]
Note: The square root of this average squared speed is called the root mean square (RMS) speed, and has the value
\[v_{rms} = \sqrt{ \langle v^2 \rangle } = \left( \dfrac{3 k_BT}{ m} \right)^{1/2} \nonumber \]
All molecules have the same kinetic energy (\(½ mv^2\)) at the same temperature, so the fraction of molecules with higher velocities will increase as m, and thus the molecular weight, decreases. Figure 27.3.3 shows the dependence of the Maxwell-Boltzmann distribution on molecule mass. On average, heavier molecules move more slowly than lighter molecules. Therefore, heavier molecules will have a smaller speed distribution, while lighter molecules will have a speed distribution that is more spread out.
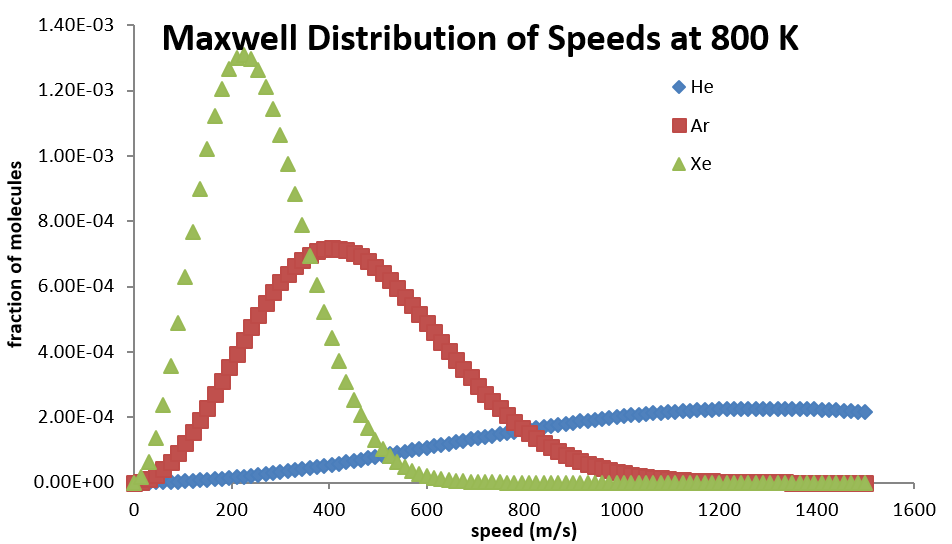
Related Speed Expressions
Usually, we are more interested in the speeds of molecules rather than their component velocities. The Maxwell–Boltzmann distribution for the speed follows immediately from the distribution of the velocity vector, above. Note that the speed of an individual gas particle is:
\[v =\sqrt{v_x^2+ v_y^2 = v_z^2} \nonumber \]
Three speed expressions can be derived from the Maxwell-Boltzmann distribution:
- the most probable speed,
- the average speed, and
- the root-mean-square speed.
The most probable speed is the maximum value on the distribution plot (Figure 27.3.4 ). This is established by finding the velocity when the derivative of Equation \(\ref{27.3.1}\) is zero
\[\dfrac{df(v)}{dv} = 0 \nonumber \]
which is
\[\color{red} v_{mp}=\sqrt {\dfrac {2RT}{M}} \label{3a} \]
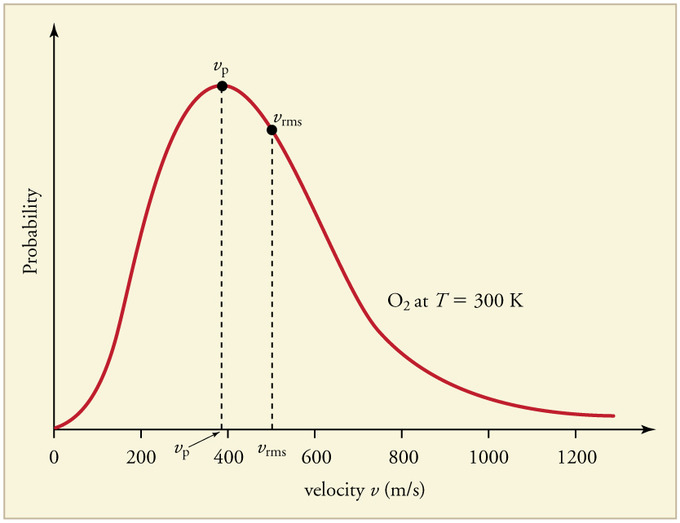
The average speed is the sum of the speeds of all the molecules divided by the number of molecules.
\[\color{red} v_{avg}= \bar{v} = \int_0^{\infty} v f(v) dv = \sqrt {\dfrac{8RT}{\pi M}} \nonumber \]
The root-mean-square speed is square root of the average speed-squared.
\[ \color{red} v_{rms}= \bar{v^2} = \sqrt {\dfrac {3RT}{M}} \nonumber \]
where
- \(R\) is the gas constant,
- \(T\) is the absolute temperature and
- \(M\) is the molar mass of the gas.
It always follows that for gases that follow the Maxwell-Boltzmann distribution:
\[v_{mp}< v_{avg}< v_{rms} \nonumber \]
Problems
- Using the Maxwell-Boltzman function, calculate the fraction of argon gas molecules with a speed of 305 m/s at 500 K.
- If the system in problem 1 has 0.46 moles of argon gas, how many molecules have the speed of 305 m/s?
- Calculate the values of \(C_{mp}\), \(C_{avg}\), and \(C_{rms}\) for xenon gas at 298 K.
- From the values calculated above, label the Boltzmann distribution plot with the approximate locations of (C_{mp}\), \(C_{avg}\), and \(C_{rms}\).
- What will have a larger speed distribution, helium at 500 K or argon at 300 K? Helium at 300 K or argon at 500 K? Argon at 400 K or argon at 1000 K?
Answers
- 0.00141
- \(3.92 \times 10^{20}\) argon molecules
- cmp = 194.27 m/s, cavg = 219.21 m/s, crms = 237.93 m/s
- As stated above, Cmp is the most probable speed, thus it will be at the top of the distribution curve. To the right of the most probable speed will be the average speed, followed by the root-mean-square speed.
- Hint: Use the related speed expressions to determine the distribution of the gas molecules: helium at 500 K. helium at at 300 K. argon at 1000 K.
Sources
- Dunbar, R.C. Deriving the Maxwell Distribution J. Chem. Ed. 1982, 59, 22-23.
- Peckham, G.D.; McNaught, I.J.; Applications of the Maxwell-Boltzmann Distribution J. Chem. Ed. 1992, 69, 554-558.
- Chang, R. Physical Chemistry for the Biosciences, 25-27.
- HyperPhysics: http://hyperphysics.phy-astr.gsu.edu...maxspe.html#c3
Contributors and Attributions
Stephen Lower, Professor Emeritus (Simon Fraser U.) Chem1 Virtual Textbook
- Adam Maley (Hope College)
Patrick E. Fleming (Department of Chemistry and Biochemistry; California State University, East Bay)
- Stephanie Schaertel (Grand Valley State University)
- Tom Neils (Grand Rapids Community College, editing)

