4.8: Gases
- Page ID
- 142227
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The Ideal Gas Law
An ideal gas is a mythical substance in which the gas particles have neither volume nor attractive intermolecular forces. Such a substance does not exist, but using the approximation creates a very simple mathematical description of a gas sample, the ideal gas law. The ideal gas law, PV = nRT, relates the four variables that describe any sample of a gas:
P is pressure, the force per unit area exerted by gas molecules as they bounce off of the surfaces that they hit. There are many units for measuring gas pressure. A unit you may have seen in a weather report is inches of mercury (in Hg), which are convenient units to use when measuring pressure with a mercury manometer. Another common unit is pounds per square inch (psi). However, we will use the unit of atmospheres (atm), an older pressure unit that was once defined as the pressure required to hold up a 760 mm column of Hg at 0oC. Colloquially, 1.00 atm is the pressure exerted by the atmosphere at sea level on an average day.
V is for volume, the amount of space that the gas sample is confined in. We will use the unit of Liters for our volume measurements.
n is for moles, the number of moles of gas particles in the sample.
T is for temperature, the property that allows us to determine the direction of heat flow and also gives us an idea of the kinetic energy of the gas molecules. We will use the Kelvin temperature scale for temperature, because we can not have any negative temperatures when describing gases. (Remember, the temperature in Kelvin = the temperature in Celsius plus 273.15o. K = 273.15 + oC.)
R is the gas constant, 0.08206 \(\dfrac{L·atm}{mole·K} \). This value can be obtained from the ratio of \(\dfrac {(22.4 \; L)(1.00 \; atm)}{(1.00 \; mole)(273.15 \; K)} \), employing the volume that 1.00 mole of an ideal gas occupies when held at 1.00 atm pressure and a temperature of 273.15 K, but it is true for any ideal gas under any set of conditions.
The ideal gas law is useful because if we know the values of any three of the four variables (P, V, T, and n) for a sample of gas, we can calculate the value of the fourth variable for that gaseous sample. The equation also allows us to predict the final state of a sample of a gas (i.e., its final temperature, pressure, volume, and amount) following any changes in conditions if the parameters (P, V, T, and n) are specified for an initial state. Some applications are illustrated in the following examples. The approach used throughout is always to start with the same equation—the ideal gas law—and then determine which quantities are given and which need to be calculated. Let’s begin with simple cases in which we are given three of the four parameters needed for a complete physical description of a gaseous sample.
Example \(\PageIndex{1}\)
A balloon with a volume of 31,150 L is to be filled with an ideal gas. If the temperature at ground level is 303 K, and the atmospheric pressure is 0.980 atm, how many moles of hydrogen gas will be needed to fill the balloon?
Given: volume, temperature, and pressure
Asked for: moles of gas
Strategy:
- Solve the ideal gas law for the unknown quantity, in this case n.
- Make sure that all quantities are given in units that are compatible with the units of the gas constant. If necessary, convert them to the appropriate units, insert them into the equation you have derived, and then calculate the number of moles of hydrogen gas needed.
Solution
\( n = \dfrac{PV}{RT} = \dfrac{(0.980 \; atm)(31150 \; L)}{(0.08206 \; \dfrac {L \; atm}{mole \; K})(303 \; K)} = 1.23 \times 10^3 moles \)
Exercise \(\PageIndex{1}\)
Suppose that an “empty” aerosol spray-paint can has a volume of 0.406 L and contains 0.0250 mol of a propellant gas such as CO2. What is the pressure of the gas at 25.0°C?
- Answer
-
1.51 L
A Practical Use of Air Pressure
A water well is an excavation or structure created in the ground by digging, driving, boring, or drilling to access groundwater in underground aquifers. The well water is often drawn by a pump (Figure \(\PageIndex{1}\)). Unfortunately, it impossible to pump water from very deep in the ground with just a surface pump. The key to understanding why is realizing that suction generated by the pump is not a force, but simply removing an opposing force to the force of air pressure which is already there. When you stick a pipe down a deep hole into a pool of water at the bottom of a well, air inside the pipe is pushing down on the water in the pipe, and air outside the pipe is pushing down on the water outside the pipe, which in turn pushes up on water inside the pipe - all is in a balance.
.jpg?revision=1&size=bestfit&width=451&height=422)
Figure \(\PageIndex{1}\): The manual water pump draws water up from a well by creating a vacuum that water rushes in to fill. Hand pump to pump water from a well in a village near Chennai in India. Image used with permission (CC BY 2.0; Sustainable Sanitation Alliance).
Let's say you remove the air inside the pipe. The water is pushed up the the same as it was before, but there is no counter acting force pushing the water down, so the water begins to rise inside the pipe (Figure \(\PageIndex{2}\)). So far so good, but the water stops rising at some height because the water is pulled down by gravity (i.e., the more water in the pipe, the more it weighs). Because the force of the air outside the pipe is not changing, eventually the weight of the water is equal to the air pressure outside the pipe. When this happens, the system is in balance again and water stops flowing.
Suction is not a force. Atmospheric pressure is the force that pushes the water up the pipe
Water is pumped from a well by creating a partial vacuum above the water by the pump. The amount of vacuum is equal to the weight of the column of water from the water table to the surface. Atmospheric pressure at sea level is 760 mm of mercury (\(1.01 \times 10^5 \,Pascals\)), which is equivalent to a 10.3-meter column of water. This is how deep water can be pumped from (with a surface pump; other pressurized pumps can go deeper).
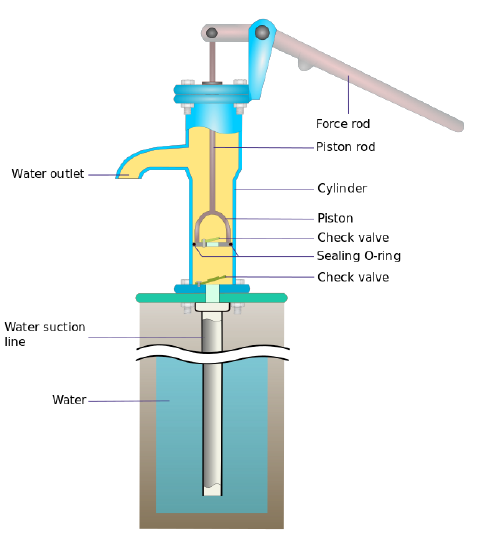
Figure \(\PageIndex{2}\): Cross section and details of a surface pump used in a well. Image used with permission (CC BY-SA 3.0; Manco Capac).
Modified by Tom Neils (Grand Rapids Community College)

