5.7: Calculating Half-Life
- Page ID
- 85164
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Describe what is meant by the term half-life and what factors affect half-life.
- Calculate the amount of radioactive material that will remain after an integral number of half-lives.
- Calculate the age of a material based upon its half-life.
- Describe how carbon-14 is used to determine the age of carbon containing objects.
- Give examples of other isotopes used in radioactive dating.
- Appreciate the half-life of isotopes involved in nuclear weapons and reactors.
Rate of Radioactive Decay
During natural radioactive decay, not all atoms of an element are instantaneously changed to atoms of another element. The decay process takes time and there is value in being able to express the rate at which a process occurs. A useful concept is half-life (symbol is \(t_{1/2}\)), which is the time required for half of the starting material to change or decay. Half-lives can be calculated from measurements on the change in mass of a nuclide and the time it takes to occur. The only thing we know is that in the time of that substance's half-life, half of the original nuclei will disintegrate. Although chemical changes were sped up or slowed down by changing factors such as temperature, concentration, etc, these factors have no effect on half-life. Each radioactive isotope will have its own unique half-life that is independent of any of these factors.
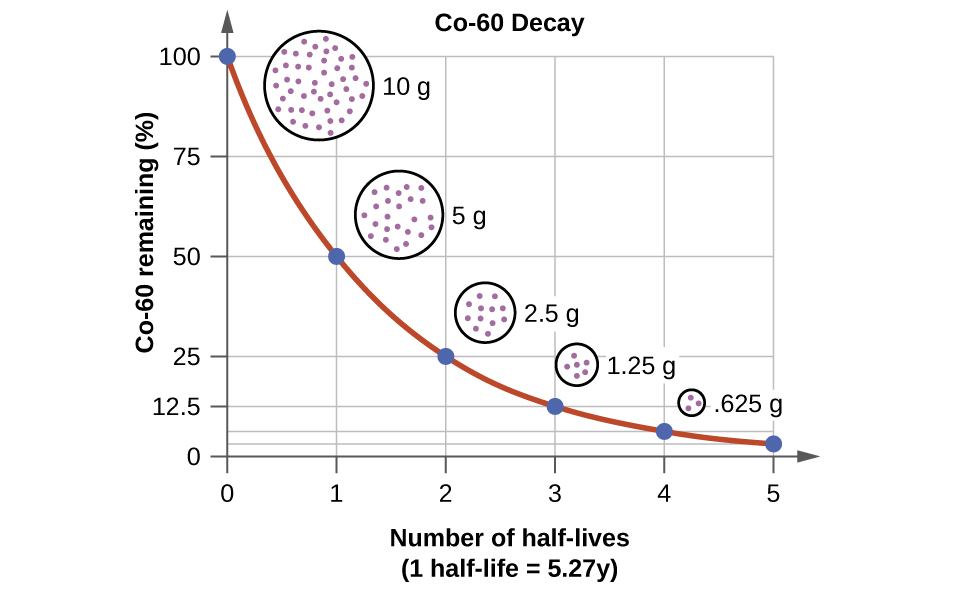
The half-lives of many radioactive isotopes have been determined and they have been found to range from extremely long half-lives of 10 billion years to extremely short half-lives of fractions of a second. The table below illustrates half-lives for selected elements. In addition, the final elemental product is listed after the decal process. Knowing how an element decays (alpha, beta, gamma) can allow a person to appropriately shield their body from excess radiation.
| Element | Mass Number (A) | Half-life | Element | Mass Number (A) | Half Life |
|---|---|---|---|---|---|
| Uranium | 238 | 4.5 Billion years | Californium | 251 | 800 years |
| Neptunium | 240 | 1 hour | Nobelium | 254 | 3 seconds |
| Plutonium | 243 | 5 hours | Carbon | 14 | 5730 years |
| Americium | 245 | 25 minutes | Carbon | 16 | 740 milliseconds |
The quantity of radioactive nuclei at any given time will decrease to half as much in one half-life. For example, if there were \(100 \: \text{g}\) of \(\ce{Cf}\)-251 in a sample at some time, after 800 years, there would be \(50 \: \text{g}\) of \(\ce{Cf}\)-251 remaining. After another 800 years (1600 years total), there would only be \(25 \: \text{g}\) remaining.
Remember, the half-life is the time it takes for half of your sample, no matter how much you have, to remain. Each half-life will follow the same general pattern as \(\ce{Cf}\)-251. The only difference is the length of time it takes for half of a sample to decay.
Click on this interactive simulation to visualize what happens to a radioisotope when it decays. and learn about different types of radiometric dating, such as carbon dating. Understand how decay and half life work to enable radiometric dating. Play a game that tests your ability to match the percentage of the dating element that remains to the age of the object.
There are two types of half-life problems we will perform. One format involves calculating a mass amount of the original isotope. Using the equation below, we can determine how much of the original isotope remains after a certain interval of time.
\[\text{how much mass remains} = \dfrac{1}{2^n} (\text{original mass}) \nonumber \]
\(n\) is the number of half-lives.
If there are 60 grams of \(\ce{Np}\)-240 present, how much \(\ce{Np}\)-240 will remain after 4 hours? (\(\ce{Np}\)-240 has a half-life of 1 hour)
Solution
\[\text{how much mass remains} = \dfrac{1}{2^4} (60 \, \text{grams}) \nonumber \]
After 4 hours, only \(3.75 \: \text{g}\) of our original \(60 \: \text{g}\) sample would remain the radioactive isotope \(\ce{Np}\)-240.
A sample of \(\ce{Ac}\)-225 originally contained \(8.0\,\,ug\). After 720 hours, how much of the original \(\ce{Ac}\)-225 remains? The half-life of this isotope is 10 days.
Solution
To determine the number of half-lives (n), both time units must be the same.
\[720\cancel{hours}\times \dfrac{1\, day}{\cancel{24 \,hours}}= 30\, days \nonumber \]
\[n=3 =\dfrac{30 \,days}{10\, days} \nonumber \]
\[\text{how much mass remains} = \dfrac{1}{2^3} (8.0 \, ug) \nonumber \]
After 720 hours, 1.0 ug of the material remains as \(\ce{Ac}\)-225
Radioactive Dating
Radioactive dating is a process by which the approximate age of an object is determined through the use of certain radioactive nuclides. For example, carbon-14 has a half-life of 5,730 years and is used to measure the age of organic material. The ratio of carbon-14 to carbon-12 in living things remains constant while the organism is alive because fresh carbon-14 is entering the organism whenever it consumes nutrients. When the organism dies, this consumption stops, and no new carbon-14 is added to the organism. As time goes by, the ratio of carbon-14 to carbon-12 in the organism gradually declines, because carbon-14 radioactively decays while carbon-12 is stable. Analysis of this ratio allows archaeologists to estimate the age of organisms that were alive many thousands of years ago.
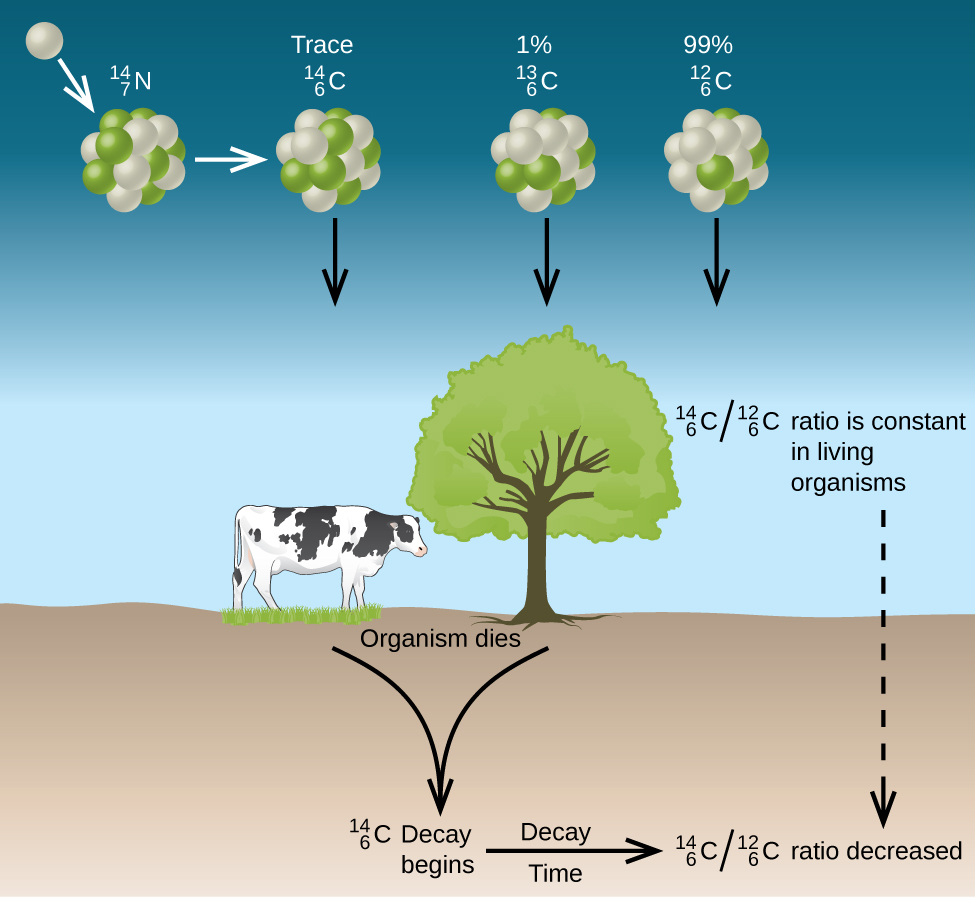
C-14 dating does have limitations. For example, a sample can be C-14 dating if it is approximately 100 to 50,000 years old. Before or after this range, there is too little of the isotope to be detected. Substances must have obtained C-14 from the atmosphere. For this reason, aquatic samples cannot be effectively C-14 dated. Lastly, accuracy of C-14 dating has been affected by atmosphere nuclear weapons testing. Fission bombs ignite to produce more C-14 artificially. Samples tested during and after this period must be checked against another method of dating (isotopic or tree rings).
To calculate the age of a substance using isotopic dating, use the equation below:
\[ \text{how old (time)} = n \times t_{1/2} \nonumber \]
\(n\) is the number of half-lives and \(t_{1/2}\) is the half-life (in time).
How long will it take for 18.0 grams of Ra-226 to decay to leave a total of 2.25 grams? Ra-226 has a half-life of 1600 years.
Solution
18.0g ⇒ 9.0g ⇒ 4.5g ⇒ 2.25g, this is three half-lives
\[ \text{how old (time)} = 3 \times 1600\, years \nonumber \]
This decay process takes 4800 years to occur.
Radioactive Dating Using Nuclides Other than Carbon-14
Radioactive dating can also use other radioactive nuclides with longer half-lives to date older events. For example, uranium-238 (which decays in a series of steps into lead-206) can be used for establishing the age of rocks (and the approximate age of the oldest rocks on earth). Since U-238 has a half-life of 4.5 billion years, it takes that amount of time for half of the original U-238 to decay into Pb-206. In a sample of rock that does not contain appreciable amounts of Pb-208, the most abundant isotope of lead, we can assume that lead was not present when the rock was formed. Therefore, by measuring and analyzing the ratio of U-238:Pb-206, we can determine the age of the rock. This assumes that all of the lead-206 present came from the decay of uranium-238. If there is additional lead-206 present, which is indicated by the presence of other lead isotopes in the sample, it is necessary to make an adjustment.
Potassium-argon dating uses a similar method. K-40 decays by positron emission and electron capture to form Ar-40 with a half-life of 1.25 billion years. If a rock sample is crushed and the amount of Ar-40 gas that escapes is measured, determination of the Ar-40:K-40 ratio yields the age of the rock. Other methods, such as rubidium-strontium dating (Rb-87 decays into Sr-87 with a half-life of 48.8 billion years), operate on the same principle. To estimate the lower limit for the earth’s age, scientists determine the age of various rocks and minerals, making the assumption that the earth is older than the oldest rocks and minerals in its crust. As of 2014, the oldest known rocks on earth are the Jack Hills zircons from Australia, found by uranium-lead dating to be almost 4.4 billion years old.
An ingenious application of half-life studies established a new science of determining ages of materials by half-life calculations. For geological dating, the decay of \(\ce{U}\)-238 can be used. The half-life of \(\ce{U}\)-238 is \(4.5 \times 10^9\) years. The end product of the decay of \(\ce{U}\)-238 is \(\ce{Pb}\)-206. After one half-life, a 1.00 gram sample of uranium will have decayed to 0.50 grams of \(\ce{U}\)-238 and 0.43 grams of \(\ce{Pb}\)-206. By comparing the amount of \(\ce{U}\)-238 to the amount of \(\ce{Pb}\)-206 in a sample of uranium mineral, the age of the mineral can be estimated. Present day estimates for the age of the Earth's crust from this method is at 4 billion years. This radioactivity approach can be used to detecting fake wine vintages too.
Isotopes with shorter half-lives are used to date more recent samples. For example, tritium (t1/2 =12.3 years) can date samples within an age range of 1-100 years. Chemists and geologists use tritium dating to determine the age of water (ocean and fresh). In addition, tritium dating can be useful in determining the age of wines and brandies.
Need More Practice?
Turn to section 5.E and work problems 11 and 13.
Contributors and Attributions
- Emma Gibney (Furman University)


