Worksheet 14: Chemical Kinetics
- Page ID
- 133041
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)
Q1
Write the rate expression in terms of \(\Delta\)[reactant]/\(\Delta\)t and \(\Delta\)[product]/\(\Delta\)t for the reaction:
\(N_2 + 3H_2 \rightarrow 2NH_3\)
Q2
The initial rate of the reaction between \(A\) and \(B\) was measured. From the data given,
- determine the order of each reactant,
- determine the order of the reaction,
- write the rate law and
- calculate the rate constant, \(k\).
| Experiment | \({[A]}\) | \({[B]}\) | initial rate |
|---|---|---|---|
| #1 | \(0.20\, M\) | \(0.10\, M\) | \(3.50 \times 10^{-3} M/s\) |
| #2 | \(0.40\, M\) | \(0.10\, M\) | \(7.00 \times 10^{-3} M/s\) |
| #3 | \(0.40\, M\) | \(0.40\, M\) | \(7.00 \times 10^{-3} M/s\) |
Q3
The decomposition of \(A_2B_3\) is second order with a \(k = 6.5 \times 10^{-5} M^{-1}s^{-1}\) at 25oC.
- If the initial concentration is \(0.50\, M\), what is the concentration after \(3 min\)?
- What is the half-life for this reaction?
Q4
- What is the concentration of reactant after 2.5 minutes if the initial concentration was \(0.100\, M\) and \(k = 6.93 \times 10^{-3} s^{-1}\) for a first order reaction?
- What is the half-life?
Q5
For the first order reaction:
\(SO_2Cl_2 \rightarrow SO_2 + Cl_2\)
How long will it take to reach \(0.31 \times 10^{-3}\, M\) if the initial concentration was \(1.25 \times 10^{-3}\; M\) and \(k = 0.17 hr^{-1}\)?
Q6
For the reaction below, if substance A is disappearing at a rate of \(1.82 \times10^{-2}\; M/s\), at what rate is C appearing?
\(3A + 3B \rightarrow 5C + 2D\)
Q7
Ozone, \(O_3\), is produced in the stratosphere by the chemical reaction shown below. If at a given instant, molecular oxygen, \(O_2\), is reacting at a rate of \(2.17 \times10^{-5}\; M/s\), at what rate is ozone being produced?
\(3O_2(g) \rightarrow 2O_3(g)\)
Q8
For the reaction,
\(H_2O_2 + 3I^- + 2H^+ \rightarrow 2H_2O + I_3^-\)
The rate law was experimentally determined to be Rate = \({k[H_2O_2][I^-]}\)
- What is the reaction order in terms of \(H_2O_2\)?
- What is the reaction order in terms of \(I^-\)?
- What is the reaction order in terms of \(H^+\)?
- What is the overall reaction order of this reaction?
Q9
If a reaction is second order in B and the concentration of B increased from \(0.0850 M\) to \(0.2975 M\), what should happen to the rate?
Q10
The data below were collected for the reaction:
\(BrO_3^- + 5Br^- + H_3O^+ \rightarrow 3Br_2 + 9H_2O\)
| Experiment # | Initial Concentrations \({(M)}\) | Initial Rate \({(M/s)}\) | |||
| \(BrO_3^-\) | \(Br^-\) | \(H_3O^+\) | \(Br_2\) | ||
| 1 | 0.10 | 0.10 | 0.10 | 0 | 1.2 |
| 2 | 0.20 | 0.10 | 0.10 | 0 | 2.4 |
| 3 | 0.10 | 0.30 | 0.10 | 0 | 3.6 |
| 4 | 0.20 | 0.10 | 0.15 | 0 | 5.4 |
- Determine the rate law for this reaction.
- Calculate the value of k for this reaction and express it with the correct units.
- How would the initial rate change if the initial concentration of \(Br_2\) were to be non-zero?
Q11
It is known that compounds called chlorofluorocarbons (CFC.s) (eg. \(CFCl_3\)) will break up in the presence of ultraviolet radiation, such as found in the upper atmosphere, forming single chlorine atoms (radicals):
\(CFCl_3 \rightarrow CFCl_2 + Cl\)
The \(Cl\) atoms then react with ozone (\(O_3\) ) as outlined in the following mechanism.
Step 1: \(Cl + O_3 \rightarrow ClO + O_2\)
Step 2: \(ClO + O \rightarrow Cl + O_2\) (single "O" atoms occur naturally in the atmosphere.)
- Write the equation for the overall reaction. (Using steps 1 and 2)
- What is the catalyst in this reaction?
- Identify an intermediate in this reaction.
- Explain how a small amount of chlorofluorocarbons can destroy a large amount of ozone.
- What breaks the bond in the \(CFCl_3\) and releases the free Cl atom?
Q12
Given the following mechanism, answer the questions below:
Step 1: \(O_3 + NO \rightarrow NO_2 + O_2\) (slow)
Step 2: \(NO_2 + O \rightarrow NO + O_2\) (fast)
- Give the equation for the overall reaction.
- What could the catalyst be in this mechanism?
- What is an intermediate in this mechanism?
- Given that the uncatalyzed overall reaction is a slow exothermic reaction, draw an energy diagram which shows the possible shape of the curve for the uncatalyzed reaction. On the same diagram, show a possible curve for the catalyzed reaction.
Q13
What is meant by the rate determining step in a reaction mechanism?
Q14
What is meant by a reaction mechanism ?
Q15
How are reaction mechanisms determined?
Q16
Given the following energy diagram for a 3-step reaction, answer the questions below:
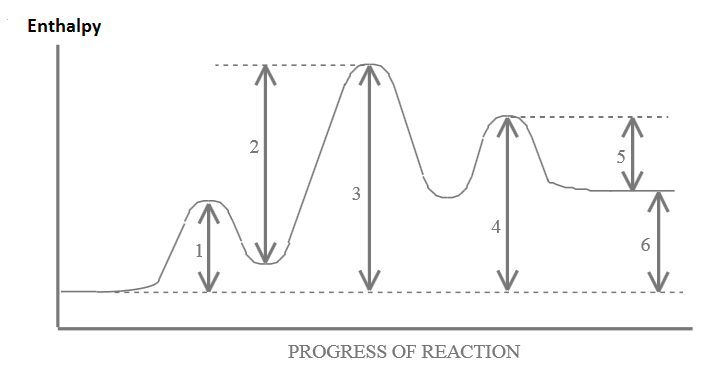
- Which arrow indicates the activation energy for the first step of the reverse reaction?
- Which arrow indicates the activation energy for the first step of the forward reaction?
- Which arrow indicates the activation energy for the second step of the forward reaction?
- Which arrow indicates the enthalpy change ( \(\Delta{H}\)) for the overall forward reaction?
- Which arrow indicates the enthalpy change ( \(\Delta{H}\)) for the overall reverse reaction?
- Which arrow indicates the activation energy for the overall forward reaction?
- Which step would be the rate determining step in the forward reaction?
- In a dashed line or another color sketch a possible curve that would represent the route for the uncatalyzed overall reaction. Label this on the graph.
Q17
Given the reaction:
\(4HBr + O_2 \rightarrow 2H_2O + 2Br_2\)
- Would you expect this reaction to take place in a single step? Why or why not?
- This reaction is thought to take place by means of the following mechanism:
Step 1: \(HBr + O_2 \rightarrow HOOBr \) (slow)
Step 2:\(HBr + HOOBr \rightarrow 2HOBr\) (fast)
Step 3: \(2HBr + 2HOBr \rightarrow 2H_2O + 2Br_2\) (fast)
- Identify the two intermediates.
- A catalyst is discovered which increases the rate of Step 3. How will this affect the rate of the overall reaction? Explain your answer.
- A catalyst is discovered which increases the rate of Step 1. How will this affect the rate of the overall reaction? Explain your answer.
- Which step has the greatest activation energy?
- How many "peaks" will the potential energy diagram for the reaction mechanism have?
- Which step is called the rate determining step in this mechanism?
- In order to have successful collisions, the colliding particles must have both the proper amount of energy and the proper _______________. (fill in blank)
- Draw an energy diagram which shows the shape of the curve you might expect for the reaction in this question. The overall reaction is exothermic. Make sure you get the "bumps" the correct relative sizes.
Q18
The equation for an overall reaction is: \(I^- + OCl^- \rightarrow IO^- + Cl^-\)
- The following is a proposed mechanism for this reaction. One of the species has been left out. Determine what that species is (in lieu of the question mark). Make sure the charge is correct if it has one.
Step 1: \(OCl^- + H_2O \rightarrow HOCl + OH^-\) (fast )
Step 2: \(I^- + HOCl \rightarrow IOH + Cl^- \) (slow )
Step 3: \(IOH + OH^- \rightarrow ? + H_2O \)(fast)
- Which species in the mechanism above acts as a catalyst ?
- Which three species in the mechanism above are intermediates?
- Which step is the rate determining step?
- Draw an energy diagram which shows the shape of the curve you might expect for the reaction in this question. The overall reaction is endothermic. Make sure you get the "bumps" the correct relative sizes.
Q19
Reaction rates and rate laws for the following gas phase reaction are given.
| \({[O_3]} = 1.0 \times 10^{14} molecules/cm^3\) | \({[NO]} = 2.0 \times 10^{14} molecules/cm^3\) | |||
|---|---|---|---|---|
| Time (ms) | \([NO]\) | Time | \([O_3]\) | |
| 0 | \(6.0 \times 10^8\) | 0 | \(1.0 \times 10^{10}\) | |
| 100 | \(5.0 \times 10^8\) | 50 | \(8.4 \times 10^9\) | |
| 500 | \(2.4 \times 10^8\) | 100 | \(7.0 \times 10^9\) | |
| 700 | \(1.7 \times 10^8\) | 200 | \(4.9 \times 10^9\) | |
| 1000 | \(9.9 \times 10^7\) | 300 | \(3.4 \times 10^9\) | |
Using the data above:
- Graph concentration vs. time for each data set.
- Graph ln[] vs. time.
- Determine the average rate for the reaction between each data point.
- Use your graph to determine the instantaneous reaction rate at 250 ms.
- Given that the reaction is first order in \(NO\) and in \(O_3\), determine the rate constant using your calculated rate for each set of data points
- Use the ln[] vs time graph to determine the rate constant.
- What is the overall rate law?
- Convert the units of the rate constant to moles, liters, and seconds.
Q20
Given the following kinetics data for the reaction in Q19:
| T (K) | \(k {(M^{-1} s^{-1})}\) |
| 195 | \(1.08 \times 10^9\) |
| 230 | \(2.95 \times 10^9\) |
| 260 | \(5.42 \times 10^9\) |
| 298 | \(12.0 \times 10^9\) |
| 369 | \(35.5 \times 10^9\) |
- Graph this data as ln(k) vs 1/T.
- Determine the activation energy and the frequency factor from the graph.
- What is the rate constant at 150 K?

