6.5: Mole-Mass and Mass-Mass Problems
- Page ID
- 68009
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
Learning Objectives
- To convert from mass or moles of one substance to mass or moles of another substance in a chemical reaction.
We have established that a balanced chemical equation is balanced in terms of moles as well as atoms or molecules. We have used balanced equations to set up ratios, now in terms of moles of materials, that we can use as conversion factors to answer stoichiometric questions, such as how many moles of substance A react with so many moles of reactant B. We can extend this technique even further. Recall that we can relate a molar amount to a mass amount using molar mass. We can use that ability to answer stoichiometry questions in terms of the masses of a particular substance, in addition to moles. We do this using the following sequence:
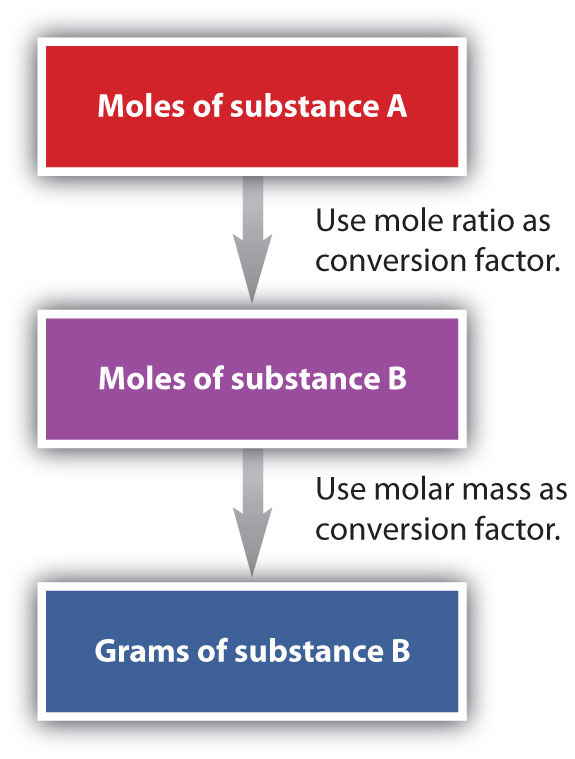
Collectively, these conversions are called mole-mass calculations.
As an example, consider the balanced chemical equation
\[Fe_2O_3 + 3SO_3 \rightarrow Fe_2(SO_4)_3 \label{Eq1}\]
If we have 3.59 mol of Fe2O3, how many grams of SO3 can react with it? Using the mole-mass calculation sequence, we can determine the required mass of SO3 in two steps. First, we construct the appropriate molar ratio, determined from the balanced chemical equation, to calculate the number of moles of SO3 needed. Then using the molar mass of SO3 as a conversion factor, we determine the mass that this number of moles of SO3 has.
As usual, we start with the quantity we were given:
\[\mathrm{3.59\: mol\: Fe_2O_3\times\dfrac{3\: mol\: SO_3}{1\: mol\: Fe_2O_3}=10.77\: mol\: SO_3} \label{Eq2}\]
The mol Fe2O3 units cancel, leaving mol SO3 unit. Now, we take this answer and convert it to grams of SO3, using the molar mass of SO3 as the conversion factor:
\[\mathrm{10.77\: mol\: SO_3\times\dfrac{80.06\: g\: SO_3}{1\: mol\: SO_3}=862\: g\: SO_3} \label{Eq3}\]
Our final answer is expressed to three significant figures. Thus, in a two-step process, we find that 862 g of SO3 will react with 3.59 mol of Fe2O3. Many problems of this type can be answered in this manner.
The same two-step problem can also be worked out in a single line, rather than as two separate steps, as follows:
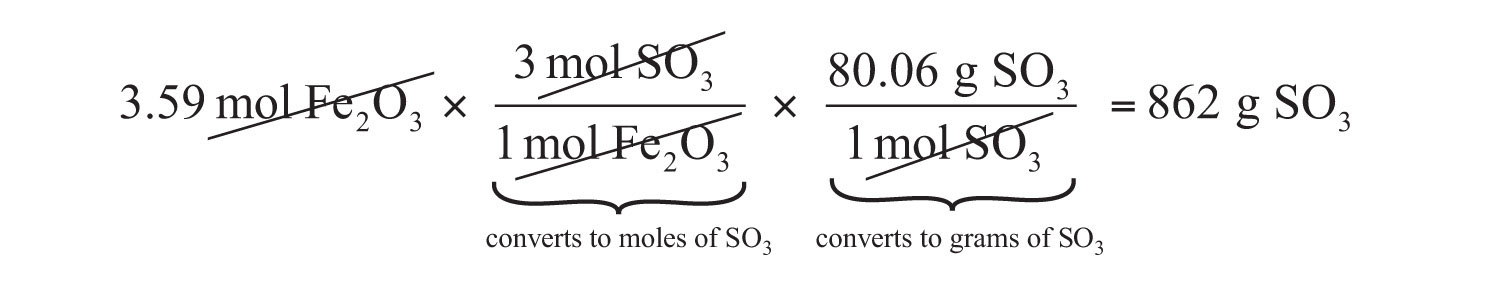
We get exactly the same answer when combining all the math steps together as we do when we calculate one step at a time.
Example \(\PageIndex{1}\)
How many grams of CO2 are produced if 2.09 mol of HCl are reacted according to this balanced chemical equation?
\[CaCO_3 + 2HCl \rightarrow CaCl_2 + CO_2 + H_2O\]
Solution
Our strategy will be to convert from moles of HCl to moles of CO2 and then from moles of CO2 to grams of CO2. We will need the molar mass of CO2, which is 44.01 g/mol. Performing these two conversions in a single-line gives 46.0 g of CO2:
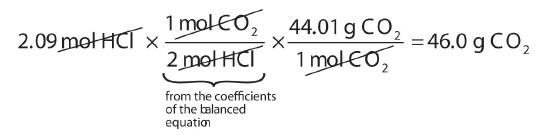
The molar ratio between CO2 and HCl comes from the balanced chemical equation.
Exercise \(\PageIndex{1}\)
How many grams of glucose (C6H12O6) are produced if 17.3 mol of H2O are reacted according to this balanced chemical equation?
\[6CO_2 + 6H_2O \rightarrow C_6H_{12}O_6 + 6O_2\]
It is a small step from mole-mass calculations to mass-mass calculations. If we start with a known mass of one substance in a chemical reaction (instead of a known number of moles), we can calculate the corresponding masses of other substances in the reaction. The first step in this case is to convert the known mass into moles, using the substance’s molar mass as the conversion factor. Then—and only then—we use the balanced chemical equation to construct a conversion factor to convert that quantity to moles of another substance, which in turn can be converted to a corresponding mass. Sequentially, the process is as follows:
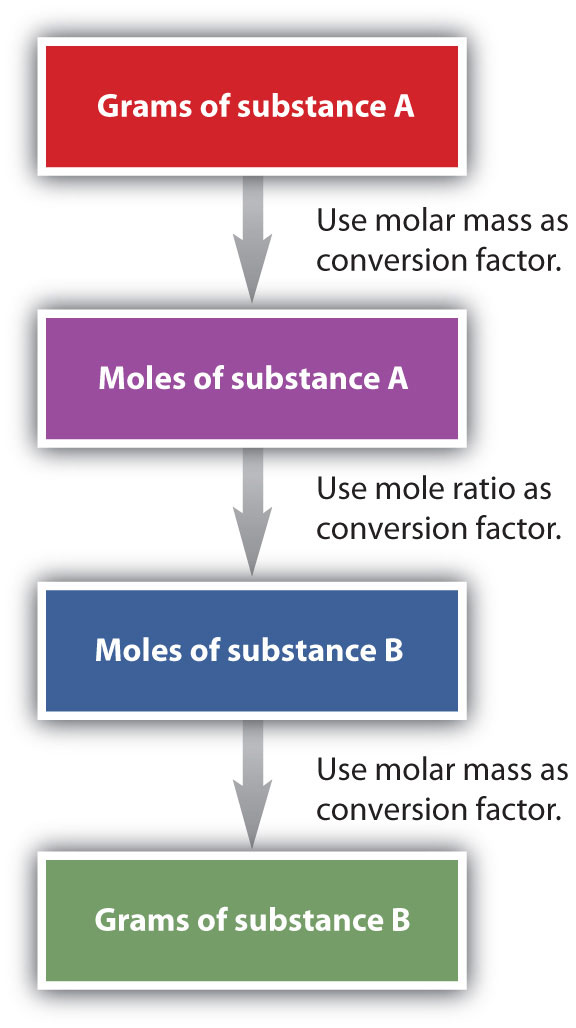
This three-part process can be carried out in three discrete steps or combined into a single calculation that contains three conversion factors. The following example illustrates both techniques.
Example \(\PageIndex{2}\): Chlorination of Carbon
Methane can react with elemental chlorine to make carbon tetrachloride (CCl4). The balanced chemical equation is as follows:
\[CH_4 + 4Cl_2 \rightarrow CCl_4 + 4HCl\]
How many grams of HCl are produced by the reaction of 100 g of CH4?
Solution
First, let us work the problem in stepwise fashion. We begin by converting the mass of CH4 to moles of CH4, using the molar mass of CH4 (16.05 g/mol) as the conversion factor:
\(\mathrm{100.0\: g\: CH_4\times\dfrac{1\: mol\: CH_4}{16.05\: g\: CH_4}=6.231\: mol\: CH_4}\)
Note that we inverted the molar mass so that the gram units cancel, giving us an answer in moles. Next, we use the balanced chemical equation to determine the ratio of moles CH4 and moles HCl and convert our first result into moles of HCl:
\(\mathrm{6.231\: mol\: CH_4\times\dfrac{4\: mol\: HCl}{1\: mol\: CH_4}=24.92\: mol\: HCl}\)
Finally, we use the molar mass of HCl (36.46 g/mol) as a conversion factor to calculate the mass of 24.92 mol of HCl:
\(\mathrm{24.92\: mol\: HCl\times\dfrac{36.46\: g\: HCl}{1\: mol\: HCl}=909\: g\: HCl}\)
In each step, we have limited the answer to the proper number of significant figures. If desired, we can do all three conversions on a single line:
\(\mathrm{100.0\: g\: CH_4\times\dfrac{1\: mol\: CH_4}{16.05\: g\: CH_4}\times\dfrac{4\: mol\: HCl}{1\: mol\: CH_4}\times\dfrac{36.46\: g\: HCl}{1\: mol\: HCl}=909\: g\: HCl}\)
Exercise \(\PageIndex{2}\): Oxidation of Propanal
The oxidation of propanal (CH3CH2CHO) to propionic acid (CH3CH2COOH) has the following chemical equation:
CH3CH2CHO + 2K2Cr2O7 → CH3CH2COOH + other products
How many grams of propionic acid are produced by the reaction of 135.8 g of K2Cr2O7?
Limiting Reactant
In all the examples discussed thus far, the reactants were assumed to be present in stoichiometric quantities. Consequently, none of the reactants was left over at the end of the reaction. This is often desirable, as in the case of a space shuttle, where excess oxygen or hydrogen was not only extra freight to be hauled into orbit but also an explosion hazard. More often, however, reactants are present in mole ratios that are not the same as the ratio of the coefficients in the balanced chemical equation. As a result, one or more of them will not be used up completely but will be left over when the reaction is completed. In this situation, the amount of product that can be obtained is limited by the amount of only one of the reactants. The reactant that restricts the amount of product obtained is called the limiting reactant. The reactant that remains after a reaction has gone to completion is in excess.
To be certain you understand these concepts, let’s first consider a nonchemical example. Assume you have invited some friends for a really cheap lunch, cheese sandwiches for everyone! The balanced equation for cheese sandwich preparation is:
2 bread + 1 cheese → 1 cheese sandwich
Go to the Reactant, Products and Leftovers Phet simulation and make some sandwiches!
Notice how when your ratio of bread to cheese is 2:1 (for example, 4 bread and 2 cheese, or 8 bread and 4 cheese), you have no leftovers. 2:1 is the stoichiometric ratio. But what happens if you have bread and cheese in quantities that don't match that ratio? Leftovers! For example, if you have 7 bread and 2 cheese, you make 4 sandwiches, with three bread and no cheese leftover. Cheese in this example is the limiting reagent, and the bread in this example is said to be 'in molar excess.'
Now consider a chemical example. Methane burns in oxygen according to this reaction equation:
\[CH_4 + 2O_2 → CO-2 + 2H_2O\]
If 1 mole of CH4 is reacted with 2 moles of O2, then there are no left overs, and one mole of CO2 and 2 moles of water are produced. But what if 2 mole of CH4 is reacted with 2 moles of O2? This is not the stoichiometric ratio of 2:1, but 2:2. Only one of those moles of methane will react by the reaction equation above, and the remainder will be left over. Oxygen in this example is the limiting reactant, and methane is in molar excess.
Key Takeaways
- A balanced chemical equation can be used to relate masses or moles of different substances in a reaction.
- Most reactions that occur in nature do not involve the reactants present in exact stoichiometric ratios. Rather one reactant will be in excess and the other will be the limiting reagent.
Concept Review Exercises
- What is the general sequence of conversions for a mole-mass calculation?
- What is the general sequence of conversions for a mass-mass calculation?
Answers
- mol first substance → mol second substance → mass second substance
- mass first substance → mol first substance → mol second substance → mass second substance
Exercises
-
Given the following unbalanced chemical equation,
H3PO4 + NaOH → H2O + Na3PO4
what mass of H2O is produced by the reaction of 2.35 mol of H3PO4?
-
Given the following unbalanced chemical equation,
C2H6 + Br2 → C2H4Br2 + HBr
what mass of HBr is produced if 0.884 mol of C2H6 is reacted?
-
Certain fats are used to make soap, the first step being to react the fat with water to make glycerol (also known as glycerin) and compounds called fatty acids. One example is as follows:
\(\mathrm{\underset{\large{a\: fat}}{C_3H_5(OOC(CH_2)_{14}CH_3)_3}+3H_2O\rightarrow \underset{\large{glycerol}}{C_3H_5(OH)_3}+\underset{\large{fatty\: acid}}{3CH_3(CH_2)_{14}COOH}}\)
How many moles of glycerol can be made from the reaction of 1,000.0 g of C3H5(OOC(CH2)14CH3)3?
-
Photosynthesis in plants leads to the general overall reaction for producing glucose (C6H12O6):
6CO2 + 6H2O → C6H12O6 + 6O2
How many moles of glucose can be made from the reaction of 544 g of CO2?
-
Precipitation reactions, in which a solid (called a precipitate) is a product, are commonly used to remove certain ions from solution. One such reaction is as follows:
Ba(NO3)2(aq) + Na2SO4(aq) → BaSO4(s) + 2NaNO3(aq)
How many grams of Na2SO4 are needed to precipitate all the barium ions produced by 43.9 g of Ba(NO3)2?
-
Nitroglycerin [C3H5(ONO2)3] is made by reacting nitric acid (HNO3) with glycerol [C3H5(OH)3] according to this reaction:
C3H5(OH)3 + 3HNO3 → C3H5(ONO2)3 + 3H2O
If 87.4 g of HNO3 are reacted with excess glycerol, what mass of nitroglycerin can be made?
-
Antacids are bases that neutralize acids in the digestive tract. Magnesium hydroxide [Mg(OH)2] is one such antacid. It reacts with hydrochloric acid in the stomach according to the following reaction:
Mg(OH)2 + 2HCl → MgCl2 + 2H2O
How many grams of HCl can a 200 mg dose of Mg(OH)2 neutralize?
-
Acid rain is caused by the reaction of nonmetal oxides with water in the atmosphere. One such reaction involves nitrogen dioxide (NO2) and produces nitric acid (HNO3):
3NO2 + H2O → 2HNO3 + NO
If 1.82 × 1013 g of NO2 enter the atmosphere every year due to human activities, potentially how many grams of HNO3 can be produced annually?
-
A simplified version of the processing of iron ore into iron metal is as follows:
2Fe2O3 + 3C → 4Fe + 3CO2
How many grams of C are needed to produce 1.00 × 109 g of Fe?
-
The SS Hindenburg contained about 5.33 × 105 g of H2 gas when it burned at Lakehurst, New Jersey, in 1937. The chemical reaction is as follows:
2H2 + O2 → 2H2O
How many grams of H2O were produced?
Answers
-
127 g
-
1.236 mol
-
23.9 g
-
0.251 g
9. 1.61 × 108 g

