4.3: High Spin and Low Spin Complexes
- Page ID
- 83495
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)High spin and low spin are two possible classifications of spin states that occur in coordination compounds. These classifications come from either the ligand field theory, which accounts for the energy differences between the orbitals for each respective geometry, or the crystal field theory, which accounts for the breaking of degenerate orbital states, compared to the pairing energy.
Introduction
To understand the ligand field theory, one must understand molecular geometries. The three molecular geometries relevant to this module are: square planar, tetrahedral, and octahedral. Besides geometry, electrons and the rules governing the filling of the orbitals are also reviewed below.
Square Planar Geometry
Square planar is the geometry where the molecule looks like a square plane. Additionally, the bond angles between the ligands (the ions or molecules bounded to the central atom) are 90o. This compound has a coordination number of 4 because it has 4 ligands bound to the central atom. An example of the square planar molecule XeF4 is provided below.

Tetrahedral Geometry
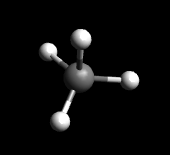
Tetrahedral geometry is a bit harder to visualize than square planar geometry. Tetrahedral geometry is analogous to a pyramid, where each of corners of the pyramid corresponds to a ligand, and the central molecule is in the middle of the pyramid. This geometry also has a coordination number of 4 because it has 4 ligands bound to it. Finally, the bond angle between the ligands is 109.5o. An example of the tetrahedral molecule CH4, or methane, is provided below.
Octahedral Geometry
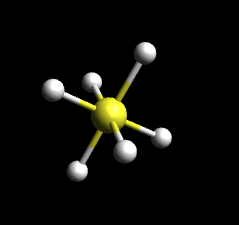
Octahedral geometry is still harder to visualize because of how many ligands it contains. Octahedral geometry can be visualized in two ways: it can be thought of as two pyramids stuck together on their bases (one pyramid is upright and the other pyramid is glued to the first pyramid's base in an upside down manner) or it can be thought of as a molecule with square planar geometry except it has one ligand sticking out on top of the central molecule and another ligand sticking out under the central molecule (like a jack). Finally, the bond angle between the ligands is 90o. An example of the octahedral molecule SF6 is provided below.
Electrons and Orbitals
When placing electrons in orbital diagrams, electrons are represented by arrows. An arrow pointing up corresponds a spin of +1/2 and an arrow pointing corresponds to a spin of -1/2. Electrons in different singly occupied orbitals of the same sub-shell have the same spins (or parallel spins, which are arrows pointing in the same direction). The sub-shell relates to the s, p, d, and f blocks that the electrons of an observed element are located. The s sub-shell has one orbital, the p sub-shell has three orbitals, the d sub-shell has five orbitals, and the f sub-shell has seven orbitals.
When filling orbitals with electrons, a couple of rules must be followed. According to the Aufbau principle, orbitals with the lower energy must be filled before the orbitals with the higher energy. Hunds rule states that all orbitals must be filled with one electron before electron pairing begins. Finally, the Pauli exclusion principle states that an orbital cannot have two electrons with the same spin. The ligand field theory and the splitting of the orbitals helps further explain which orbitals have higher energy and in which order the orbitals should be filled.
Ligand Field Theory
The ligand field theory is the main theory used to explain the splitting of the orbitals and the orbital energies in square planar, tetrahderal, and octahedral geometry. The ligand field theory states that electron-electron repulsion causes the energy splitting between orbitals. It states that the ligand fields may come in contact with the electron orbitals of the central atom, and those orbitals that come in direct contact with the ligand fields have higher energy than the orbitals that come in indirect contact with the ligand fields. This is because when the orbital of the central atom comes in direct contact with the ligand field, a lot of electron-electron repulsion is present as both the ligand field and the orbital contain electrons. Remember, opposites attract and likes repel. Thus, due to the strong repelling force between the ligand field and the orbital, certain orbitals have higher energies than others. One thing to keep in mind is that this energy splitting is different for each molecular geometry because each molecular geometry can hold a different number of ligands and has a different shape to its orbitals.
Spin
A complex can be classified as high spin or low spin. When talking about all the molecular geometries, we compare the crystal field splitting energy (\(\Delta\)) and the pairing energy (\(P\)). Normally, these two quantities determine whether a certain field is low spin or high spin.
When the crystal field splitting energy is greater than the pairing energy, electrons will fill up all the lower energy orbitals first and only then pair with electrons in these orbitals before moving to the higher energy orbitals. Electrons tend to fall in the lowest possible energy state, and since the pairing energy is lower than the crystal field splitting energy, it is more energetically favorable for the electrons to pair up and completely fill up the low energy orbitals until there is no room left at all, and only then begin to fill the high energy orbitals. On the other hand, when the pairing energy is greater than the crystal field energy, the electrons will occupy all the orbitals first and then pair up, without regard to the energy of the orbitals. If every orbital of a lower energy had one electron, and the orbitals of the hext higher energy had none, an electron in this case would occupy the higher energy orbital. This follows Hund's rule that says all orbitals must be occupied before pairing begins. Remember, this situation only occurs when the pairing energy is greater than the crystal field energy. These phenomena occur because of the electron's tendency to fall into the lowest available energy state.
Another method to determine the spin of a complex is to look at its field strength and the wavelength of color it absorbs. If the field is strong, it will have few unpaired electrons and thus low spin. If the field is weak, it will have more unpaired electrons and thus high spin. In terms of wavelength, a field that absorbs high energy photons (in other words, low wavelength light) has low spin and a field that absorbs low energy photons (high wavelength light) has high spin.
Once again, whether a complex is high spin or low spin depends on two main factors: the crystal field splitting energy and the pairing energy. The electrons will take the path of least resistance--the path that requires the least amount of energy. If the paring energy is greater than \(\Delta\), then electrons will move to a higher energy orbital because it takes less energy. If the pairing energy is less than \(\Delta\), then the electrons will pair up rather than moving singly to a higher energy orbital. Below, tips and examples are given to help figure out whether a certain molecule is high spin or low spin.
Is the \([Co(H_2O)_6]^{3+}\) complex ion expected to be high or low spin?
Solution
What do we know?
- The complex has an octahedral shape
- The aqua ligand (\(H_2O\)) is typically regarded as weak-field ligand
- The d electron configuration for \(Co\) is \(d^6\)
- The splitting energy is small
Therefore, the complex is expected to be high spin.
Do you expect the \([Ni(CN)_4]^{2-}\) complex ion to be high or low spin?
Solution
What do we know?
- The complex has a square planar shape
- \(CN^-\) is a strong-field ligand
- The d electron configuration for Ni is \(d^8\)
- The splitting energy is large
Therefore, the complex is low spin.
Do you expect the \([CoF_6]^{3-}\) complex ion to be high or low spin?
Solution
What do we know?
- The complex has an octahedral shape
- F- is a weak-field ligand
- The d electron configuration for Co is d6
- The splitting energy is small
Therefore, the complex is high spin.
Spectrochemical Series
Another tool used often in calculations or problems regarding spin is called the spectrochemical series. The spectrochemical series is a list that orders ligands on the basis of their field strength. Ligands that have a low field strength, and thus high spin, are listed first and are followed by ligands of higher field strength, and thus low spin. This trend also corresponds to the ligands abilities to split d orbital energy levels. The ones at the beginning, such as I−, produce weak splitting (small Δ) and are thus weak field ligands. The ligands toward the end of the series, such as CN−, will produce strong splitting (large Δ) and thus are strong field ligands. A picture of the spectrochemical series is provided below.
(weak) I− < Br− < S2− < SCN− < Cl− < NO3− < N3− < F− < OH− < C2O42− ≈ H2O <
NCS− < CH3CN < py < NH3 < en < bipy < phen < NO2− < PPh3 < CN− ≈ CO (strong)
Octahedral Complexes
Octahedral complexes have a coordination number of 6, meaning that there are six places around the metal center where ligands can bind. Interactions between the electrons of the ligands and those of the metal center produce a crystal field splitting where the dz2 and dx2-y2 orbitals raise in energy, while the other three orbitals of dxz, dxy, and dyz, are lower in energy. This results from the interaction between the orbitals and the ligand field. The ligand field runs almost right into the dz2 and dx2-y2 orbitals, thus having direct contact with these two orbitals. Due to this direct contact, a lot of electron-electron repulsion occurs between the ligand fields and the dz2 and dx2-y2 orbitals, which results in the dz2 and dx2-y2 orbitals having high energy, as the repulsion has to be manifested somewhere. The ligand field only brushes through the other three dxz, dxy, and dyz orbitals. Since the ligand field does not have such direct contact with these orbitals and since there is not as much resulting electron-electron repulsion, the dxz, dxy, and dyz orbitals have lesser energy than the dz2 and dx2-y2 orbitals. It is this difference in energy between the dz2 and dx2-y2 orbitals and the dxz, dxy, and dyz orbitals that is known as crystal field splitting.
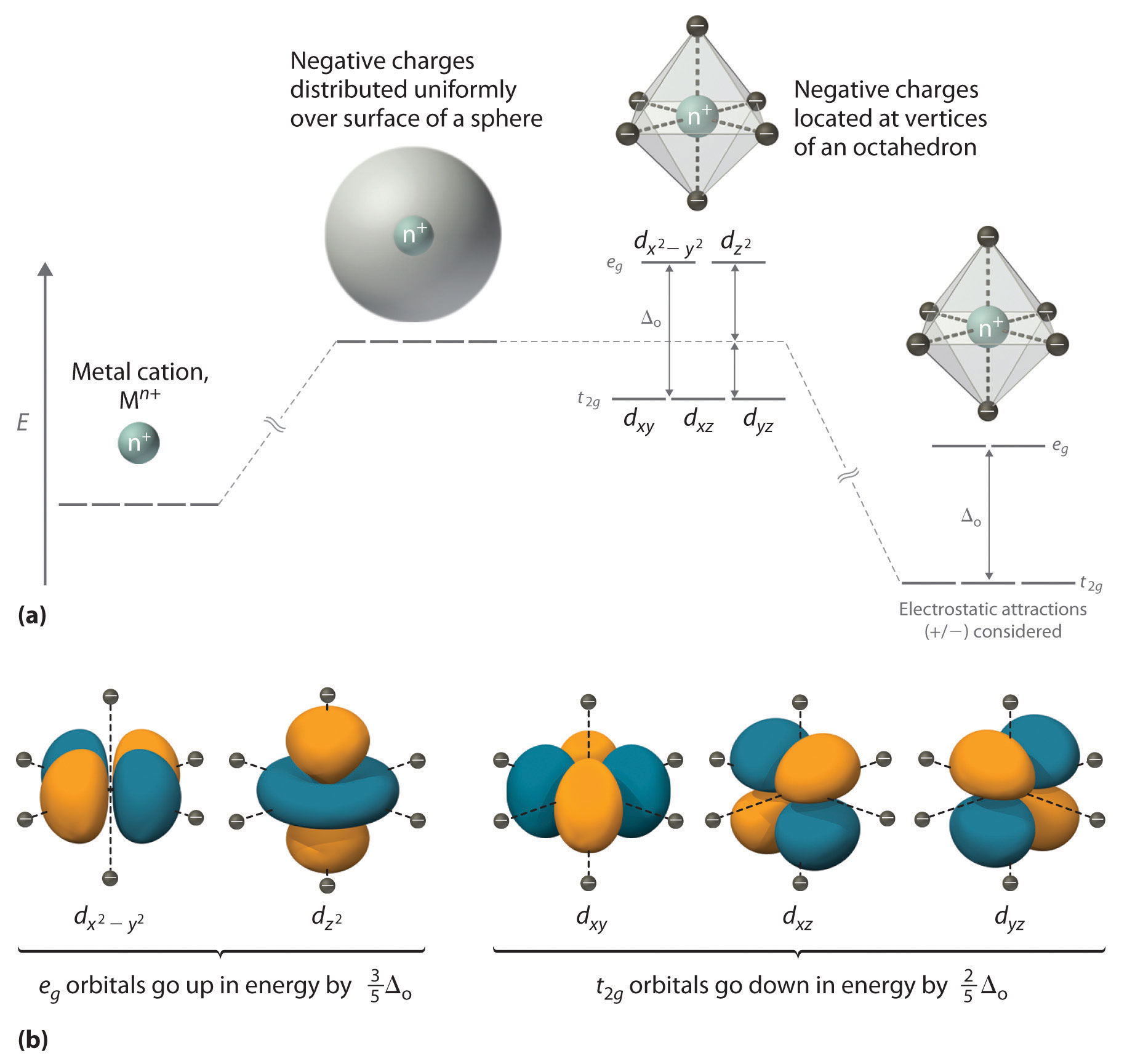
Figure 1: Octahedral Complex Splitting:
In an octahedral complex, when Δ is large (strong field ligand), the electrons will first fill the lower energy d orbitals before any electrons are placed on the higher energy d orbitals. It is then classified as low spin because there is a minimal amount of unpaired electrons. When Δ is small, the pairing energy exceeds the splitting energy, and the electrons will fill the d orbitals as if they were degenerate; this is classified as high spin.
The oxidation state of the metal also determines how small or large Δ is. The higher the oxidation state of the metal, the stronger the ligand field that is created. In the event that there are two metals with the same d electron configuration, the one with the higher oxidation state is more likely to be low spin than the one with the lower oxidation state.
Usually, the field strength of the ligand, which is also determined by large or small Δ, determines whether an octahedral complex is high or low spin. This is where we use the spectrochemical series to determine ligand strength. Strong-field ligands, like CN- and NO2-, increase Δ which results in low spin. While weak-field ligands, like I- and Cl-, decrease the Δ which results in high spin.
Tetrahedral Complexes
The splitting of tetrahedral complexes is directly opposite that of the splitting of the octahedral complexes. Recall that in octahedral complexes, the dz2 and dx2-y2 orbitals have higher energy than the dxz, dxy, and dyz orbitals. In tetrahedral complexes, the opposite occurs because the dxz, dxy, and dyz orbitals have higher energy than the dz2 and dx2-y2 orbitals. This is once again because the contact between the ligands and the orbitals is reverse that of octahedral complexes. Unlike octahedral complexes, the ligands of tetrahedral complexes come in direct contact with the dxz, dxy, and dyz orbitals. Thus, these orbitals have high electron-electron repulsion, due to the direct contact, and thus higher energy. The dz2 and dx2-y2 orbitals do not have as direct contact as the ligands kind of squeeze past or slide by these orbitals, thus lowering the electron-electron repulsion and the energy of the orbital.
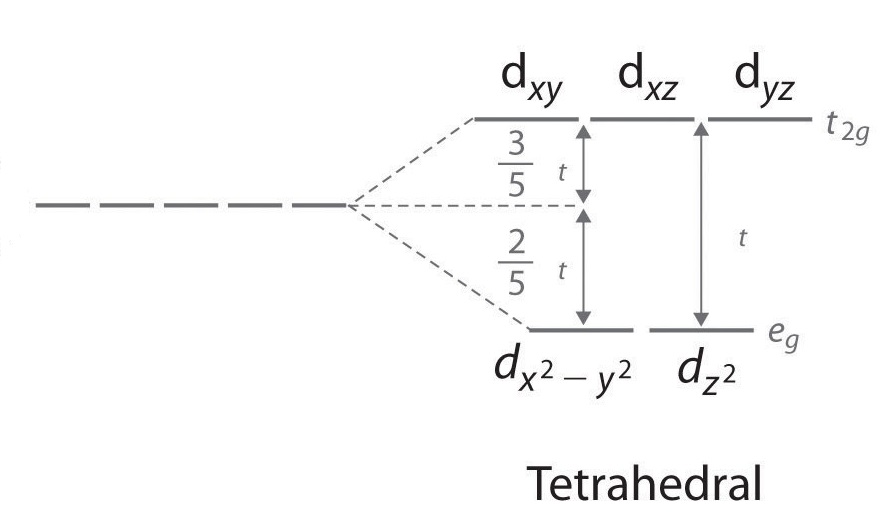
Figure 2: Tetrahedral Complex Splitting:
In a tetrahedral complex, Δt is relatively small even with strong-field ligands as there are fewer ligands to bond with. It is rare for the Δt of tetrahedral complexes to exceed the pairing energy. Usually, electrons will move up to the higher energy orbitals rather than pair. Because of this, most tetrahedral complexes are high spin.
Square Planar Complexes
A square planar complex also has a coordination number of 4. The structure of the complex differs from tetrahedral because the ligands form a simple square on the x and y axes. Because of this, the crystal field splitting is also different. Since there are no ligands along the z-axis in a square planar complex, the repulsion of electrons in the dxz, dyz, and the dz2 orbitals are considerably lower than that of the octahedral complex (the dz2 is slightly higher in energy to the "doughnut" that lies on the x,y axis). The dx2-y2 orbital has the most energy, followed by the dxy orbital, which is followed by the remaining orbtails (although dz2 has slightly more energy than the dxz and dyz orbital). This pattern of orbital splitting remains constant throughout all geometries. Whichever orbitals come in direct contact with the ligand fields will have higher energies than orbitals that slide past the ligand field and have more of indirect contact with the ligand fields. So when confused about which geometry leads to which splitting, think about the way the ligand fields interact with the electron orbitals of the central atom.
In square planar complexes Δ will almost always be large, even with a weak-field ligand. Electrons tend to be paired rather than unpaired because paring energy is usually much less than Δ. Therefore, square planar complexes are usually low spin.
Tips For Determining High Spin or Low Spin Configurations
- Determine the shape of the complex (i.e. octahedral, tetrahedral, square planar)
- Determine the oxidation state of the metal center
- Determine the d electron configuration of the metal center
- Draw the crystal field diagram of the complex with regards to its geometry
- Determine whether the splitting energy is greater than the pairing energy
- Determine the strength of the ligand (i.e. spectrochemical series)
Crystal Field Splitting Electron Count
In order to make a crystal field diagram of a particular coordination compound, one must consider the number of electrons. This can be done simply by recognizing the ground state configuration of the electron and then adjusting the number of electrons with respect to the charge of the metal. For example, one can consider the following chemical compounds. These four examples demonstrate how the number of electrons are determined and used in making Crystal Field Diagrams.
What is the number of electrons of the metal in this complex: [CoF6]3- ?
Solution
This coordination compound has Cobalt as the central transition metal and 6 Fluoro monodentate ligands. However, in this example as well as most other examples, we will focus on the central transition metal. We must determine the oxidation state of Cobalt in this example. Fluorine has a charge of -1 and the overall molecule has a charge of -3. Since there are six fluorines, the overall charge of fluorine is -6. The charge of Cobalt will add to this -6, so that the charge of the overall molecule is -3. Thus, we know that Cobalt must have a charge of +3 (see below). The electron configuration of Cobalt is [Ar]4s23d7. When observing Cobalt 3+, we know that Cobalt must lose three electrons. The first two to go are from the 4s orbital and Cobalt becomes:[Ar]4s03d7. Then, the next electron leaves the 3d orbital and the configuration becomes: [Ar]4s03d6. Thus, we can see that there are six electrons that need to be apportioned to Crystal Field Diagrams. The pairing of these electrons depends on the ligand. Since Fluorine is a weak field, it will be a high spin complex.
Cobalt charge Fluorine charge Overall charge
x + -1(6) = -3
x + -6 = -3
x=-3+6
x=+3
What is the number of electrons of the metal in this complex: [Co(NH3)6]3+?
Solution
This coordination compound has Cobalt as the central Transition Metal and 6 Ammonias as Monodentate Ligands. We must determine the oxidation state of Cobalt in this example. Ammonia has a charge of 0 and the overall molecule has a charge of +3. Since there are six Ammonias the overall charge of of it is 0. The charge of Cobalt will add to this 0, so that the charge of the overall molecule is +3. Thus, we know that Cobalt must have a charge of +3 (see below). In order to find the number of electrons, we must focus on the central Transition Metal. The electron configuration of Cobalt is [Ar]4s23d7. When observing Cobalt 3+, we know that Cobalt must lose three electrons. The first two to go are from the 4s orbital and Cobalt becomes:[Ar]4s03d7. Then, the next electron leaves the 3d orbital and the configuration becomes: [Ar]4s03d6. Thus, we can see that there are six electrons that need to be apportioned to Crystal Field Diagrams. The pairing of these electrons depends on the ligand. Since Ammonia is a strong field ligand, it will be a low spin complex.
Cobalt charge Ammonia charge Overall charge
x + 0(6) = +3
x + 0 = +3
x=+3
What is the number of electrons of the metal in this complex: [Fe(CN)6]3-?
Solution
This coordination compound has Iron as the central Transition Metal and 6 Cyanides as Monodentate Ligands. We must determine the oxidation state of Iron in this example. Cyanide has a charge of -1 and the overall molecule has a charge of -3. Since there are six Cyanides the overall charge of of it is -6. The charge of Iron will add to this -6, so that the charge of the overall molecule is -3. Thus, we know that Iron must have a charge of +3 (see below). In order to find the number of electrons, we must focus on the central Transition Metal. The electron configuration of Iron is [Ar]4s23d6. When observing Iron 3+, we know that Iron must lose three electrons. The first two to go are from the 4s orbital and Iron becomes:[Ar]4s03d6. Then, the next electron leaves the 3d orbital and the configuration becomes: [Ar]4s03d5. Thus, we can see that there are five electrons that need to be apportioned to Crystal Field Diagrams. The pairing of these electrons depends on the ligand. Since Cyanide is a strong field ligand, it will be a low spin complex.
Iron charge Cyanide charge Overall charge
x + -1(6) = -3
x + -6 = -3
x=-3+6
x=+3
[Ni(CN)4]2-
Solution
This coordination compound has Nickel as the central Transition Metal and 4 Cyanides as Monodentate Ligands. We must determine the oxidation state of Nickel in this example. Cyanide has a charge of -1 and the overall molecule has a charge of -2. Since there are four Cyanides, the overall charge of it is -4. The charge of Nickel will add to this -4, so that the charge of the overall molecule is -2. Thus, we know that Nickel must have a charge of +2 (see below). In order to find the number of electrons, we must focus on the central transition metal. The electron configuration of Nickel is [Ar]4s23d8. When observing Nickel 3+, we know that Nickel must lose two electrons. The two to go are from the 4s orbital and Nickel becomes:[Ar]4s03d8. Thus, we can see that there are eight electrons that need to be apportioned to Crystal Field Diagrams. The pairing of these electrons depends on the ligand. Since Cyanide is a strong field ligand, it will be a low spin complex.
Nickel charge Cyanide charge Overall charge
x + -1(4) = -2
x + -4 = -2
x=-2+4
x=+2
Applications
Magnetism
The crystal field splitting can also be used to figure out the magnetism of a certain coordination compound. Recall, that diamagnetism is where all the electrons are paired and paramagnetism is where one or more electron is unpaired. This property can be used to determine the magnetism and in some cases the filling of the orbitals. For example, given a high spin octahedral molecule, one just has to fill in all the orbitals and check for unpaired electrons. If no unpaired electrons exist, then the molecule is diamagnetic but if unpaired molecules do exist, the molecule is paramagnetic. These properties of magnetism can also be used to predict how the orbitals will be filled, an alternate method to relying on spin to predict the filling of orbitals. For example, if a given molecule is diamagnetic, the pairing must be done in such a way that no unpaired electrons exist. On the other hand, if the given molecule is paramagnetic, the pairing must be done in such a way that unpaired molecules do exist. Examples of these properties and applications of magnetism are provided below.
Color
Crystal field splitting can be used to account for the different colors of the coordinate compounds. Low spin complexes with strong field ligands absorb light at shorter wavelengths (higher energy) and high spin complexes with weak field ligands absorb light at longer wavelengths (lower energy). Based on the ligands involved in the coordination compound, the color of that coordination compound can be estimated using the strength the ligand field. See Tanabe-Sugano Diagrams for more advanced applications.
Sample Problems
Questions
- Is square planar usually low spin or high spin?
- Draw the crystal field energy diagram of [Cu(Cl)6]-4.
- What is the spectrochemical series?
- Draw the crystal field energy diagram of [Mn(CN)4]-1.
- What causes the energy difference between the orbitals in an octahedral field?
- Classify the spin of [FeBr4]-2.
Answers
- Due to the high crystal field splitting energy, square planar complexes are usually low spin.
- By doing some simple algebra and using the -1 oxidation state of chloro ligand and the overall charge of -4, we can figure out that the oxidation state of copper is +2 charge. In its non-ionized state, copper has the following electron distribution: [Ar]4s13d10. +2 means that copper will loose two electrons and will thus have a configuration of [Ar]3d9. Using the spectrochemical series, we can figure out that the chloro ligand is a weak field and induces low spin complex. How this is meaningless this problem since the appropriate crystal field energy diagram shows that only one configuration is possible irrespective of the strength of the ligand field:

- The spectrochemical series is a series that orders ligands based on their field strength. It is often used in problems to determine the strength and spin of a ligand field so that the electrons can be distributed appropriately.
- Just like problem 2, the first thing to do is to figure out the charge of Mn. Since we know the CN has a charge of -1, and there are four of them, and since the overall molecule has a charge of -1, manganese has a oxidation state of +3. In its ground state, manganese has the following electron distribution: [Ar]4s23d5. The +3 oxidation state means that manganese will loose three electrons and will thus have a configuration of [Ar]3d4. Using the spectrochemical series, we can figure out the strength of the CN ligand field, which is a strong field ligand and induces low spin complexes. The appropriate crystal field energy diagram would look like:
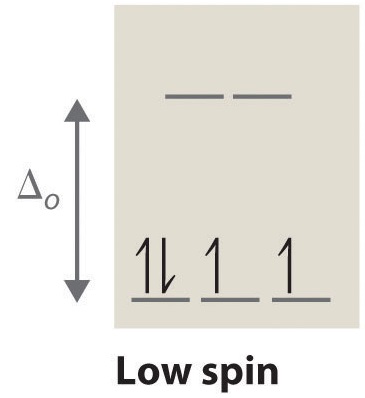
- The negative-negative repulsion between the electrons of the central atom and between the ligand field causes certain orbitals, namely the dz2 and dx2-y2 orbitals, to have higher energy than the dxz, dxy, and dyz orbitals.
- Since the bromo ligand is a weak field ligand (as per the spectrochemical series), this molecule is high spin.
External Links
- Orbitals and electron configuration review part one of two. http://www.youtube.com/watch?v=M7fgT-hI6jk
- Orbitals and electron configuration review part two of two. http://www.youtube.com/watch?v=9frZH1UsY_s&feature=related
- Electronic structure of coordination complexes. http://www.youtube.com/watch?v=mAPFhZpnV58
Resources
- Petrucci, Ralph H. General Chemistry Principles and Modern Applications. 9th ed. Upper Saddle River: Pearson Prentice Hall, 2002, Chapter 24
- Rodgers, Glen E. Descriptive Inorganic, Coordination, and Solid-State Chemistry. 2nd ed. McGraw-Hill: New York, 1994, Chapter
Contributors and Attributions
- Angad Oberoi (UCD), Justin Nuckles (UCD)

