4.1: Colors of Coordination Complexes
- Page ID
- 83493
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The color for a coordination complex can be predicted using the Crystal Field Theory (CFT). Knowing the color can have a number of useful applications, such as the creation of pigments for dyes in the textile industry. The tendency for coordination complexes to display such a wide array of colors is merely coincidental; their absorption energies happen to fall within range of the visible light spectrum. Chemists and physicists often study the color of a substance not to understand its sheer appearance, but because color is an indicator of a chemical's physical proprieties on the atomic level.
The Electromagnetic Spectrum
The electromagnetic spectrum (EM) spectrum is made up of photons of different wavelengths. Photons, unique in displaying the properties of both waves and particles, create visible light and colors in a small portion of the EM spectrum. This visible light portion has wavelengths in approximately the 400-700 nanometer range (a nanometer, “nm,” is 10-9 meters). Each specific wavelength corresponds to a different color (see Figure 1), and when all the wavelengths are present, it appears as white light.
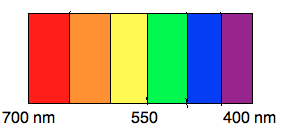
Figure 1
The wavelength and frequency of a wave are inversely proportional: as one gets increases, the other decreases; this is a consequence of all light traveling at the same speed. Because of this relationship, blue light has a much higher frequency and more energy than red light. In general, photons to the right of the EM spectrum have increasingly higher energy than photons to the left.
Perceiving Color
Color is perceived in two ways, through additive mixing, where different colors are made by combining different colors of light, and through subtractive mixing, where different wavelengths of light are taken out so that the light is no longer pure white. For colors of coordination complexes, subtractive mixing is considered. As shown in Figure 2, the idea behind subtractive mixing is that white light (which is made from all the colors mixed together) interacts with an object. The object absorbs some of the light, and then reflects or transmits (or both, depending on the object) the rest of the light, which contacts the eye. The object is perceived as whichever color is not absorbed. In Figure 2, white light (simplified as green, red, and blue bands) is shone through a solution. The solution absorbs the red and green wavelengths; however, the blue light is reflected and passes through, so the solution appears blue. This procedure takes place whenever an object displays visible color. If none of the light is absorbed, and all is reflected back off, the object appears white; if all of the light is absorbed, and there is none left to reflect or transmit through, the object appears black.
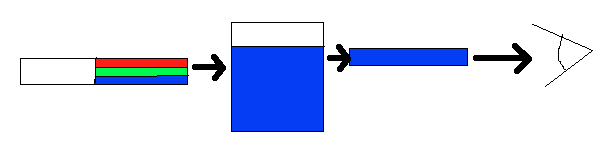
Figure 2
Colors of Coordination Complexes: Crystal Field Splitting
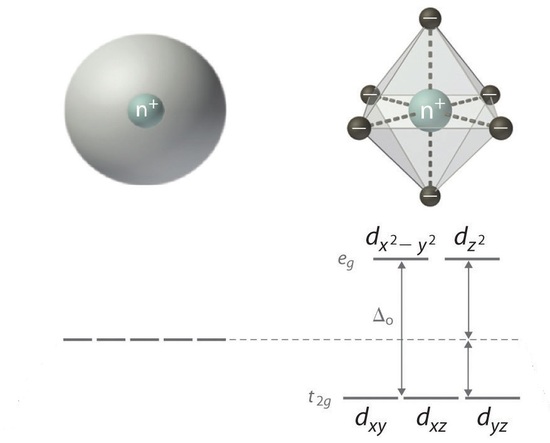
When ligands attach to a transition metal to form a coordination complex, electrons in the d orbital split into high energy and low energy orbitals. The difference in energy of the two levels is denoted as ∆, and it is a characteristic a property both of the metal and the ligands. This is illustrated in Figure 3; the "o" subscript on the ∆ indicates that the complex has octahedral geometry.
Figure 3: d-Orbitals Splitting in an octahedral ligand field
If ∆o is large, and much energy is required to promote electrons into the high energy orbitals, the electrons will instead pair in the lower energy orbitals, resulting in a "low spin" complex (Figure 4); however, if ∆o is small, and it takes little energy to occupy the higher orbitals, the electrons will do so, and remain unpaired (until there are more than five electrons), resulting in a “high spin” complex (Figure 5). Different ligands are associated with either high or low spin—a "strong field" ligand results in a large ∆o and a low spin configuration, while a "weak field" ligand results in a small ∆o and a high spin configuration. For more details, see the Crystal Field Theory (CFT) page.
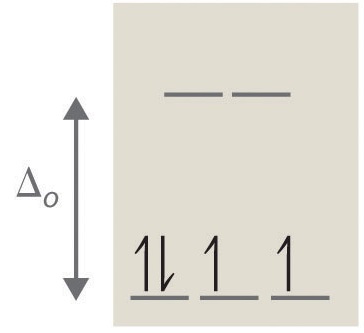
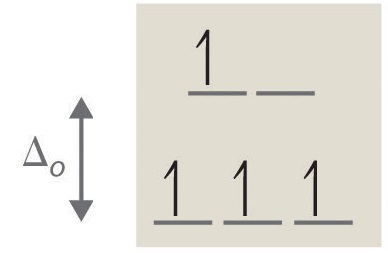
Figure 4: Low Spin, Strong Field (∆o˃P) Figure 5: High Spin, Weak Field (∆o˂P)
A photon equal to the energy difference ∆o can be absorbed, promoting an electron to the higher energy level. As certain wavelengths are absorbed in this process, subtractive color mixing occurs and the coordination complex solution becomes colored. If the ions have a noble gas configuration, and have no unpaired electrons, the solutions appear colorless; in reality, they still have a measured energy and absorb certain wavelengths of light, but these wavelengths are not in the visible portion of the EM spectrum and no color is perceived by the eye.
In general, a larger ∆ indicates that higher energy photons are absorbed, and the solution appears further to the right on the EM spectrum shown in Figure 1. This relationship is described in the equation ∆=hc/λ, where h and c are constants, and λ is the wavelength of light absorbed.
Using a color wheel can be useful for determining what color a solution will appear based on what wavelengths it absorbs (Figure 6). If a complex absorbs a particular color, it will have the appearance of whatever color is directly opposite it on the wheel. For example, if a complex is known to absorb photons in the orange range, it can be concluded that the solution will look blue. This concept can be used in reverse to determine ∆ for a complex from the color of its solution.
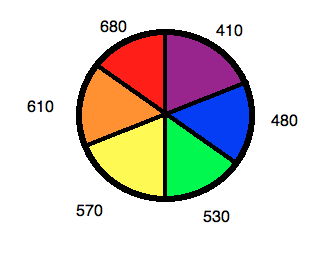 Figure 6
Figure 6
Relating the Colors of Coordination Complexes to the Spectrochemical Series
According to the Crystal Field Theory, ligands that have high spin are considered "weak field" and ligands that have low spin are considered "strong field." This relates to the colors seen in a coordination complex. High spin ligands induce the absorption of longer wavelength (lower frequency=lower energy) light than complexes with low spin ligands since their respective \(\Delta_o\) values are smaller than the electron pairing energy.
The energy difference, \(\Delta_o\), determines the color of the coordination complex. According to the spectrochemical series, the high spin ligands are considered "weak field," and absorb longer wavelengths of light (weak \(\Delta_o\)), while complexes with low spin ligands absorb light of greater frequency (high \(\Delta_o\)). The color seen is the complementary color of that of the wavelength absorbed. To predict which possible colors and their corresponding wavelengths are absorbed, the spectrochemical series can be used:
(Strong field/large Δ0/low spin) (weak field/ small Δ0/high spin)
CO-, NO-, CN->NO2->en>py≈NH3>EDTA4->SCN->H2O>ONO->ox2->OH->F->SCN->Cl->Br->I-
Example \(\PageIndex{1}\):
If a solution with a dissolved octahedral complex appears yellow to the eye, what wavelength of light does it absorb? Is this complex expected to be low spin or high spin?
SOLUTION
A solution that looks yellow absorbs light that is violet, which is roughly 410 nm from the color wheel. Since it absorbs high energy, the electrons must be raised to a higher level, and \(\Delta_o\) is high, so the complex is likely to be low spin.
Example \(\PageIndex{2}\):
An octahedral metal complex absorbs light with wavelength 535 nm. What is the crystal field splitting \(\Delta_o\) for the complex? What color is it to the eye?
SOLUTION
To solve this question, we need to use the equation
\[\Delta_o =\dfrac{hc}{\lambda}\]
with
- \(h\) is Planck’s constant and is \(6.625 \times 10^{-34} J \cdot s\) and
- \(c\) is the speed of light and is \(2.998 \times 10^8\, m/s\).
It is also important to remember that 1 nm is equal to \(1 \times 10^{-9}\) meters. With all this information, the final equation looks like this:
\[\Delta_o =\dfrac{(6.625 \times 10^{-34}\, J \cdot s)(2.998 \times 10^8\, m/s)}{(535nm) \left(\dfrac{1\,m}{1 \times 10^9\, nm}\right)}= 3.712 \,J/molecule\]
It is not necessary to use any equations to solve the second part of the problem. Light that is 535 nm is green, and because green light is absorbed, the complex appears red (refer to Figures 1 and 6 for this information).
Note: the fact that the complex is octahedral makes no impact when solving this problem. Although the splitting is different for complexes of different structures, the mechanics of solving the problem are identical.
Example \(\PageIndex{3}\):
There are two solutions, one orange and one blue. Both solutions are known to be made up of a cobalt complex; however, one has chloride ions as ligands, while the other has ammonia ligands. Which solution is expected to be orange?Solution
In order to solve this problem, it is necessary to know the relative strengths of the ligands involved. A sample ligand strength list is given here, but see Crystal Field Splitting for a more complete list: CN- > en > NH3 > H2O > F- >SCN- > Cl-
From this information, it is clear that NH3 is a stronger ligand than Cl-, which means that the complex involving NH3 has a greater ∆, and the complex will be low spin. Because of the larger ∆, the electrons absorb higher energy photons, and the solution will have the appearance of a lower energy color. Since orange light is less energetic than blue light, the NH3 containing solution is predicted to be orange
References
- Cox, P. A. Instant Notes Inorganic Chemistry. Second ed. Grand Rapids: Garland, Incorporated, 2004.
- Nassau, Kurt. The Physics and Chemistry of Color : The Fifteen Causes of Color. Second ed. New York: Wiley-Interscience, 2001.
- Petrucci, Ralph H., William S. Harwood, and Geoff E. Herring. General Chemistry : Principles and Modern Applications. Ninth ed. Upper Saddle River: Prentice Hall PTR, 2006.
- Petrucci, Ralph H., Carey Bissonnette, F. Geoffrey Herring, Jeffrey D. Madura. General Chemistry: Principles and Modern Applications. Tenth Ed. Upper Saddle River: Pearson Education, Inc. 2011.
Problems
- What color will a complex be that absorbs light that is 600 nm be?
- What color will a complex an octahedral complex appear if it has a \(\Delta_o\) of \(3.75 \times 10^{-19}\, J\)?
- Would you expect a violet solution to be high spin or low spin? What about a red solution?
- There are two solutions, one which is yellow and another which is violet. The solutions are [Co(H2O)6]3+and [Co(CN-)6]3-. What are the colors of each solution?
Answers
- Blue. The color absorbed is orange.
- It is red. Using Δ=hc/λ, h=6.626*10-34J*s, c=2.998*108m/s, wavelength would equal 530 nm. So green is absorbed, and the complementary color of green is red, so red is the color of the complex.
- It would be high spin. The complementary color of violet is yellow, which has a wavelength of 570 nm. For a red solution, the complementary color absorbed is green, with a wavelength of 530 nm, so it would be considered low spin.
- [Co(H2O)6]3+ is violet and [Co(CN-)6]3- is yellow. Looking at the spectrochemical series, H2O is a weak field ligand, so it absorbs colors of long wavelengths—in this case, the longer wavelength is yellow, so the color reflected is violet. CN- is a strong field ligand, so it absorbs colors of shorter wavelengths-in this case, the shorter wavelength is violet, so the color reflected is yellow.
Contributors
- Deyu Wang (UCD)