10.3: Why is \(BeH_2\) Linear and \(H_2O\) Bent?
- Page ID
- 63712
In this section, we will construct approximate molecular orbitals for a water molecule by considering a simple linear triatomic of the general form \(HXH\), where \(X\) is a second row element. We will take a multi-centered molecular orbital approach instead of the two-centered valence bond/hybrid approach discussed previously. As with previous discussions of Molecular Orbitals, we approximate them as a linear combinations of atomic orbitals (LCAO). In molecular orbital theory linear combinations of all available (atomic) orbitals will form molecular orbitals. These are spread over the whole molecule, or delocalized, and in a quantum chemical interpretation they are called canonical orbitals. Since it is absolutely wrong to assume that there are only three types of \(sp^x\) hybrid orbitals, it is possible, that there are multiple different types of orbitals involved in bonding for a certain atom.
AH₂ Molecules
We want to construct a reasonable argument for the energetic ordering and structure of the molecular orbitals. We first note that each \(H\) will donate a \(1s\) orbital in the LCAO scheme, and \(A\) will likely donate at least \(2s\) and possible \(2p\) orbitals, depending on its chemical identity. In general, if we consider only the first row \(A\) elements, the molecule orbitals (via the LCAO) can be expressed as combination of \(1s\) orbitals on the two Hydrogens (\(H_1\) and \(H_2\)) and the four n=2 orbitals (\(2s\; 2p_x\; 2p_y; 2p_z\)) on the \(A\) atom:
\[ | \chi \rangle = a_1 | 1s \rangle _{H_1} + a_2 | 1s \rangle _{H_2} + a_3 | 2s \rangle _{A} + a_4 | 2p_x \rangle _{A} + a_5 | 2p_y \rangle _{A} + a_6 | 2p_z \rangle _{A} \label{MO1} \]
These molecular orbitals were created with six atomic orbitals and hence six different \( | \chi \rangle \) molecular orbitals can be created. As with previous molecular orbitals problems, the coefficients of this expansion (\(\{a_i\}\)) are determined by solving the secular determinant.
If we consider only linear \(AH_2\) molecules, then Equation \(\ref{MO1}\) can be simplified by ignoring \( 2p_x\) and \(2p_y\) atomic orbitals since they are perpendicular to the bonds and are hence non-bonding (only for linear \(AH_2\) molecules). Moreover, the molecule is symmetric about the center (the position of \(A\)), hence the orbitals have to have the same symmetry.
Only the \(2p\) orbital of \(A\) that will overlap with \(1s\) of \(H\) is the \(2p_z\). Hence, Equation \(\ref{MO1}\) can be simplified to consider the combination
\[ | \chi \rangle = a_1 | 1s \rangle _{H_1} + a_1 | 1s \rangle _{H_2} + a_3 | 2s \rangle _{A} + a_6 | 2p_z \rangle _{A} \label{MO2} \]
Note that the two coefficients in front of the \(1s\) orbitals of hydrogen are the same by symmetry. This since no hydrogen is "special" and they must have the same contribution to the molecular orbital.
How big should the \(2s\) orbital contributors of \(A\) be compared to the \(1s\) orbital of \(H\)?
This depends on several things. First, is the nuclear charge on \(A\) and the second is the electronegativity difference between \(H\) and \(A\). The first determines how quickly the \(2s\) orbitals, remembering that the exponential part is \(exp(-Zr/a_0)\), and the electronegativity difference determines the relative magnitude of \(H_1\) compared to \(H_2\).
The six \(| \chi \rangle \) molecular orbitals from Equation \(\ref{MO1}\) are shown in Figure 10.3.1 .
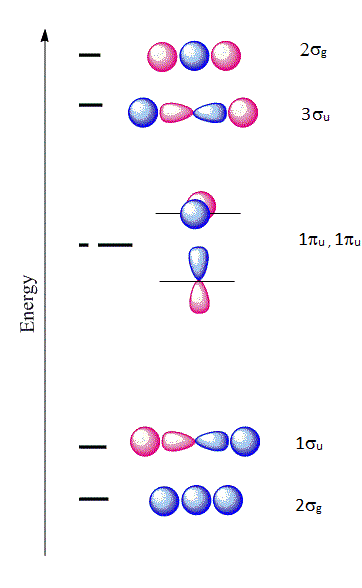
The first molecular orbital \(|\chi_1 \rangle\) constructed from Equation \(\ref{MO1}\) is purely bonding because the \(2s\) orbital is positive near the \(A\) nucleus, but becomes negative as we go away from the nucleus. This orbital is also even (garade symmetry), so we can denote it as a \(2\sigma_{g}\) orbital signifying that it is constructed from a \(2s\) orbital of \(A\) combined with the two \(1s\) orbitals of \(H\). The only other MO that can be constructed that has the right symmetry is \(|\chi_6 \rangle\) which is denoted as \(2\sigma_{u}\). This is an antibonding molecular orbital and is also even (garade symmetry). The corresponding wavefunctions are:
\[ | \chi_1 \rangle = a_1 | 1s \rangle _{H_1} + a_1 | 1s \rangle _{H_2} + a_3 | 2s \rangle _{A} \nonumber \]
\[ | \chi_6 \rangle = a_1 | 1s \rangle _{H_1} + a_1 | 1s \rangle _{H_2} - a_3 | 2s \rangle _{A} \nonumber \]
Next, if we combine a \(2p_z\) orbital of \(A\) with the \(1s\) of \(H\), there are two possibilities that have the right symmetry. The first is
\[ | \chi_2 \rangle = a_1 | 1s \rangle _{H_1} + a_1 | 1s \rangle _{H_2} + a_6 | 2p_z \rangle_{A} \nonumber \]
which is a bonding orbital and denoted as \(1\sigma_{u}\). This is purely antibonding and has an odd symmetry (ungarede). The other combination is
\[ | \chi_5 \rangle = a_1 | 1s \rangle _{H_1} - a_1 | 1s \rangle _{H_2} + a_6 | 2p_z \rangle_{A} \nonumber \]
Hence, we denote this as \(2\sigma_{g}\). The orbitals \(2p_x\) and \(2p_y\) from \(X\) are nonbonding and become \(\pi_{2p_x}\) and \(\pi_{2p_y}\) nonbonding orbitals and designated as \(1\pi_u\) orbitals:
\[ | \chi_3 \rangle = | 2p_x \rangle_{A} \nonumber \]
\[ | \chi_4 \rangle = | 2p_y \rangle_{A} \nonumber \]
Beryllium Hydride (\(BeH_2\)) is Linear
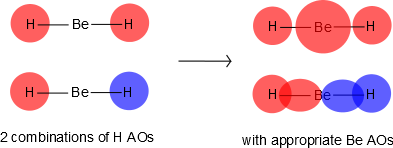
Consider the \(BeF_2\) molecule: Be has a \(1s^2\, 2s^2\) electron configuration with is no unpaired electrons available for bonding. From a perspective of using only atomic orbitals to generate the bonding orbitals, we would conclude that the molecule could not exist since no free orientals exist on \(Be\) to bond. Clearly, atomic orbitals are not adequate to describe orbitals in molecules, but this can be solved by allowing the 2s and one 2p orbital on Be to mix to form \(sp\) hybrid orbitals. The experimental H-Be-H bond angle is 180°. Presumably, one electron from Be is shared with each unpaired electrons from H. We could promote and electron from the 2s orbital on Be to the 2p orbital to get two unpaired electrons for bonding (predicting 90° bond angles, not 180°). Thus the geometry is still not explained with atomic orbitals alone.
Be has 2s and 2p orbitals, and it is in the middle. H has 1s orbitals; there are 2 H atoms on the outside. We initially make combinations of the H atomic orbitals that we previously used to make diatomic hydrogen, except there is no overlap (i.e., \(S=0\)). These combinations will mix with the 2s and 2pz on Be, as shown in Figure 10.3.2 .
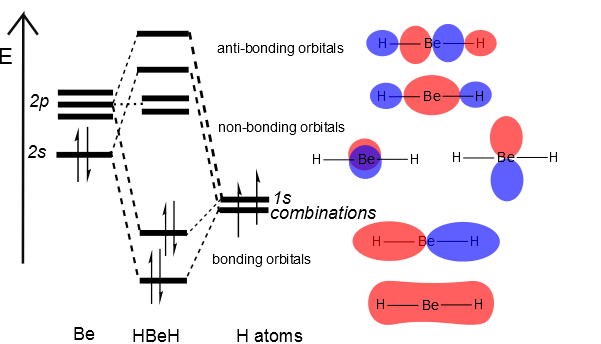
Then we can put the Molecular Orbital diagram together, starting with the outside, drawing in bonding, non-bonding and anti-bonding MOs, and filling the electrons (Figure 10.3.3 ). The bond order is 2.
Walsh diagrams, often called angular coordinate diagrams or correlation diagrams, are representations of calculated orbital energies of a molecule versus a distortion coordinate, used for making quick predictions about the geometries of small molecules. By plotting the change in molecular orbital levels of a molecule as a function of geometrical change, Walsh diagrams explain why molecules are more stable in certain spatial configurations (i.e. why water adopts a bent conformation).
A major application of Walsh diagrams is to explain the regularity in structure observed for related molecules having identical numbers of valence electrons (i.e. why \(\ce{H2O}\) and \(\ce{H2S}\) look similar), and to account for how molecules alter their geometries as their number of electrons or spin state changes. Additionally, Walsh diagrams can be used to predict distortions of molecular geometry from knowledge of how the LUMO (Lowest Unoccupied Molecular Orbital) affects the HOMO (Highest Occupied Molecular Orbital) when the molecule experiences geometrical perturbation. Walsh's rule for predicting shapes of molecules states that a molecule will adopt a structure that best provides the most stability for its HOMO. If a particular structural change does not perturb the HOMO, the closest occupied molecular orbital governs the preference for geometrical orientation.
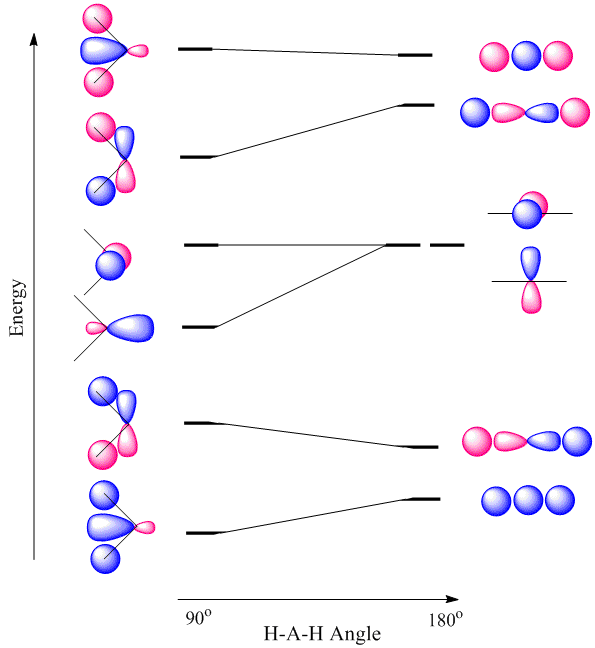
For the \(AH_2\) molecular system, Walsh produced the first angular correlation diagram by plotting the orbital energy curves for the canonical molecular orbitals while changing the bond angle from 90° to 180° (Figure 10.3.4 ). As the bond angle is distorted, the energy for each of the orbitals can be followed along the lines, allowing a quick approximation of molecular energy as a function of conformation.
A typical prediction result for water is an bond angle of 90°, which is not even close to the experimental value of 104°. At best, the method is able to differentiate between a bent and linear molecule.
Walsh's rule for predicting shapes of molecules states that a molecule will adopt a structure that best provides the most stability for its HOMO. If a particular structural change does not perturb the HOMO, the closest occupied molecular orbital governs the preference for geometrical orientation.
Figure 10.3.4 illustrates the difference between the actual linear case we just analyzed and the truly bent molecule, e.g. \(H_2 O\). The geometry changes the ordering somewhat, but the qualitative picture we obtain from the linear case makes it a useful construction. The oxygen atomic orbitals are labeled according to their symmetry (Figure 10.3.5 ) as \(a_1\) for the 2s orbital and \(b_1\) (\(2p_x\)), \(b_2\) (\(2p_y\)) and \(a_1\) (\(2p_z\)) for the three 2p orbitals. The two hydrogen 1s orbitals are premixed to form \(a_1\) and \(b_2\) molecular orbitals.
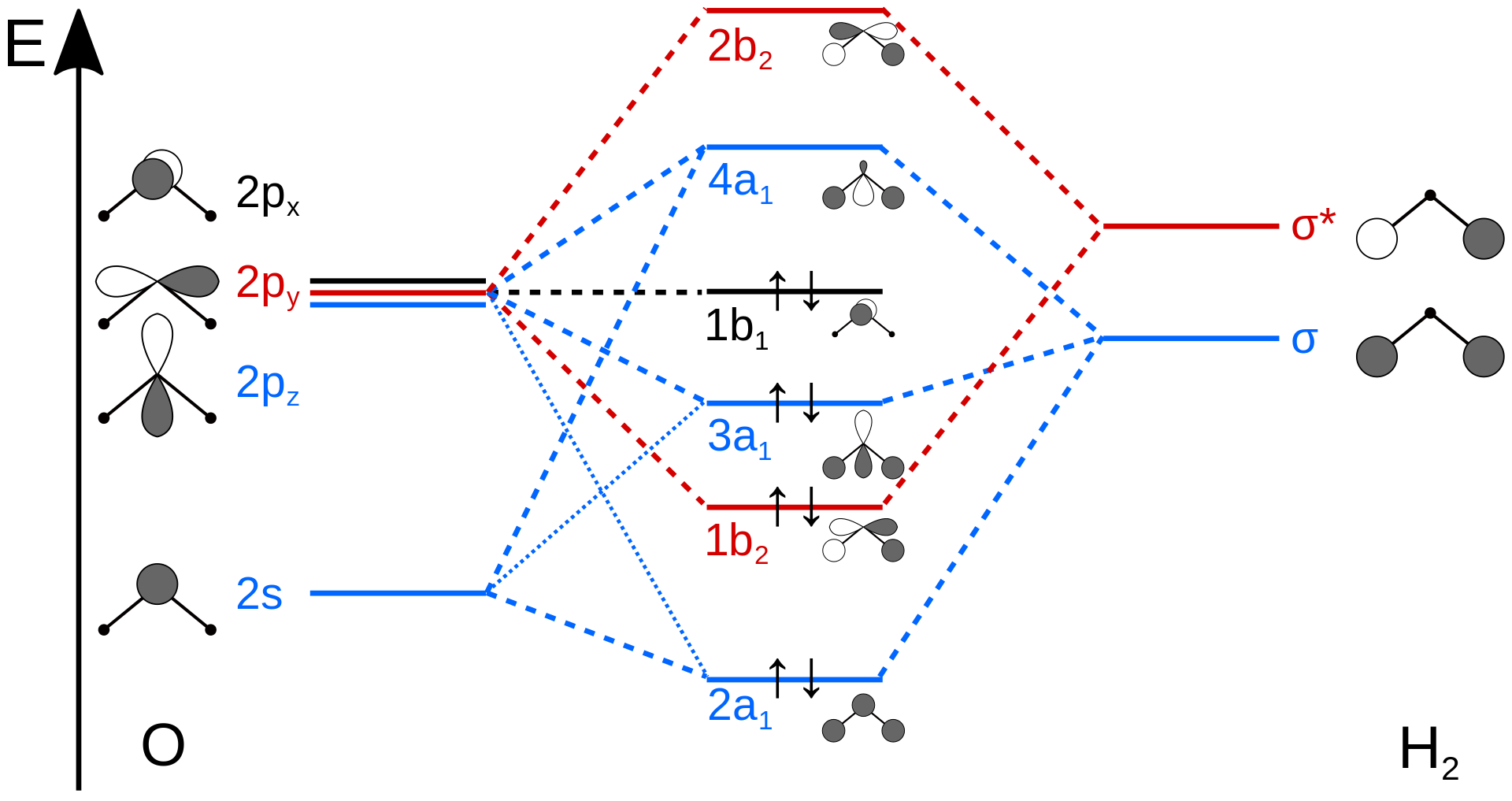
Mixing takes place between same-symmetry orbitals of comparable energy resulting a new set of MO's for water:
- 2a1 MO from mixing of the oxygen 2s atomic orbital and the hydrogen σ MO. Small oxygen 2pz atomic orbital admixture strengthens bonding and lowers the orbital energy.
- 1b2 MO from mixing of the oxygen 2py atomic orbital and the hydrogen σ* MO.
- 3a1 MO from mixing of the oxygen 2pz atomic orbital and the hydrogen σ MO. Small oxygen 2s atomic orbital admixture weakens bonding and raises the orbital energy.
- 1b1 nonbonding MO from the oxygen 2px atomic orbital (the p-orbital perpendicular to the molecular plane).
In the water molecule the highest occupied orbital, (\(1b_1\)) is non-bonding and highly localized on the oxygen atom, similar to the non-bonding orbitals of hydrogen fluoride. The next lowest orbital (\(2a_1\)) can be thought of as a non-bonding orbital, as it has a lobe pointing away from the two hydrogens. From the lower energy bonding orbitals, it is possible to see that oxygen also takes more than its "fair share" of the total electron density. The electronic configuration of water in the ground state (Figure 10.3.5 ) is therefore
\[(a_1)^2(b_2)^2(a_1)^2(b_1)^2 \nonumber \]
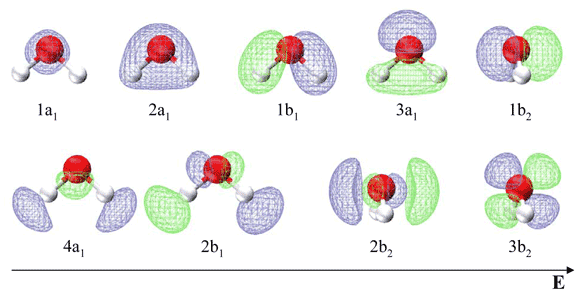
Table 10.3.1 list the respective LCAO coefficients for the six atomic orbitals. Table 10.3.1 combines the energy values with the description derived from the character table for molecules of point group C2v
| Energy | Symbol | s(H) | s(O) | px(O) | py(O) | pz(O) | s(H) |
|---|---|---|---|---|---|---|---|
|
6.728
|
2b2 |
0.525
|
0
|
0
|
-0.669
|
0
|
-0.525
|
|
5.440
|
3a1 |
-0.553
|
0.306
|
0
|
0
|
-0.544
|
0.553
|
|
-12.191
|
1b1 |
0
|
0
|
-1.000
|
0
|
0
|
0
|
|
-14.467
|
2a1 |
-0.309
|
0.354
|
0
|
0
|
0.827
|
-0.309
|
|
-19.113
|
1b2 |
-0.473
|
0
|
0
|
-0.743
|
0
|
0.473
|
|
-40.032
|
1a1 |
0.315
|
0.884
|
0
|
0
|
-0.143
|
0.315
|
Note in contrast to the valence bond theory discussed previous for water, the two lone electron pairs are not in identical orbitals. The 1b1 MO is a lone pair, while the 3a1, 1b2 and 2a1 MO's can be localized to give two O−H bonds and an in-plane lone pair. This is in agreement with the experimentally measured photoelectron spectrum discussed in the next section.
Summary
Walsh correlation diagram is a plot of molecular orbital energy as a function of some systematic change in molecular geometry. For example, the correlation between orbital energies and bond angle for an \(AH_2\) molecule. The geometry of a molecule is determined by which possible structure is lowest in energy. We can use the Walsh diagram to determine the energy trends based on which orbitals are occupied.
Contributors and Attributions
Emily V Eames (City College of San Francisco)

