10.1: Hybrid Orbitals Account for Molecular Shape
- Page ID
- 63710
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Introduce hybrid orbital to explain non-linear molecular structure
Valence bond (VB) theory is one of two basic theories, along with molecular orbital (MO) theory, that were developed to use the methods of quantum mechanics to explain chemical bonding. It focuses on how the atomic orbitals of the dissociated atoms combine to give individual chemical bonds when a molecule is formed. In contrast, molecular orbital theory, which will be discussed elsewhere, predict wavefunctions that cover the entire molecule.
Review of Diatomics
Let us consider \(H_2\). Recall that the Lewis structure for a single \(H\) atom is \(H\cdot\) and for \(H_2\), it is \(H:H\). Thus, each hydrogen brings one unpaired electron to the bond. Let the two protons be denoted A and B and the two electrons 1 and 2. Now, consider the potential energy
\[\begin{align} V &= V_{ee}+V_{en}+V_{nn}\\[4pt] &=\dfrac{e^2}{4\pi \epsilon_0}\left [ \dfrac{1}{r_{12}}-\dfrac{1}{r_{1A}}-\dfrac{1}{r_{1B}}-\dfrac{1}{r_{2A}}-\dfrac{1}{r_{2B}}+\dfrac{1}{R_{AB}}\right ] \end{align} \nonumber \]
But as \(R_{AB}\rightarrow \infty\), the \(1/r_{12}\), \(1/r_{1B}\), \(1/r_{2A}\), and \(1/R_{AB}\) terms vanish and the potential energy becomes simply that of two noninteracting hydrogen atoms
\[V\rightarrow -\dfrac{e^2}{4\pi \epsilon_0}\left [ \dfrac{1}{r_{1A}}+\dfrac{1}{r_{2B}}\right ] \nonumber \]
Since the potential energy becomes a simple sum of separate energies for electrons 1 and 2, the wavefunction should simply be a product \(\psi_{1s}(r_1 -r_A)\psi_{1s}(r_2 -r_B)\). But as we let \(R_{AB}\rightarrow R_e\), where \(R_e\) is the equilibrium bond length, the electrons mix, and we can no longer tell if electron 1 belongs to atom A or atom B and the same for electron 2. Thus, we need to construct a combination of products that is consistent with the Pauli exclusion principle. If we just consider the coordinates \(r_1\) and \(r_2\) of the electrons, then the only wavefunction we can construct from a product of 1s orbitals is
\[\psi_u (r_1 ,r_2)=C_u [\psi_{1s}^{A}(r_1)\psi_{1s}^{B} (r_2)-\psi_{1s}^{A}(r_2)\psi_{1s}^{B}(r_1)] \nonumber \]
where the \(u\) designator indicates that this is an odd function. The constant \(C_u\) is the overall noramlization constant. Unfortunately, like in the LCAO method, such a wavefunction is antibonding and is not a good representation of the ground state. If, however, we construct the wavefunction
\[\psi_g (r_1 ,r_2)=C_g [\psi_{1s}^{A} (r_1)\psi_{1s}^{B} (r_2)+\psi_{1s}^{A}(r_2) \psi_{1s}^{B} (r_1)] \nonumber \]
(where \(g\) designates that this is an even function), we violate the Pauli exclusion principle, even though such a wavefunction leads to a stable chemical bond.
What is missing here is the fact that we have not considered the spins of the electrons. Since the electrons are identical, if we exchange coordinates and spins, then the wavefunction should change sign. Thus, we can make both wavefunctions above consistent with the Pauli exclusion principle by multiplying by an appropriate spin wavefunction. We obtain
\[\begin{align}\psi_u (r_1 ,r_2 ,s_1 ,s_2 ) &=\psi_u(x_1 ,x_2)=C_u [\psi_{1s}^{A}(r_1)\psi_{1s}^{B}(r_2)-\psi_{1s}^{A}(r_2)\psi_{1s}^{B}(r_1)][\psi_{\uparrow}(s_1)\psi_{\downarrow}(s_2)+\psi_{\uparrow}(s_2)\psi_{\downarrow}(s_1)]\\[4pt] \psi_g (r_1 ,r_2 ,s_1 ,s_2) &= \psi_g(x_1 ,x_2)=C_g[\psi_{1s}^{A}(r_1)\psi_{1s}{B}(r_2)+\psi_{1s}^{A}(r_2)\psi_{1s}^{B}(r_1)][\psi_{\uparrow}(s_1)\psi_{\downarrow}(s_2)-\psi_{\uparrow}(s_2)\psi_{\downarrow}(s_1)]\end{align} \nonumber \]
where \(s_1\) and \(s_2\) are the z-components of spin for electrons 1 and 2, respectively. We can now use \(\psi_g\) as an approximate 2-electron wavefunction that leads to a stable chemical bond in \(H_2\).
The fact that \(\psi_u\) is antibonding can be easily determined by looking for a nodal plane between the two atoms, in this case, in the plane that exactly bisects the line joining the two atoms, midway between them. That this is, indeed, a nodal plane can be seen by considering two points \(r_1\) and \(r_2\) for the two electrons that are taken to lie in this plane. By symmetry, the functions \(\psi_{1s}^{A}(r_1)\) and \(\psi_{1s}^{B}(r_1)\) have the same value for \(r_1\) in this plane, and the same for \(\psi_{1s}^{B}(r_2)\) and \(\psi_{1s}^{A}(r_2)\). Let us assign the following values:
\[\begin{align}\psi_{1s}^{A}(r_1) &= \psi_{1s}^{B}(r_1)=A\\[4pt] \psi_{1s}^{B}(r_2) &= \psi_{1s}^{A}(r_2)=A' \end{align} \nonumber \]
Substituting these into \(\psi_u (x_1 ,x_2)\), we obtain
\[\psi_u (x_1 ,x_2)=C_u [AA' -A' A][\psi_{\uparrow}(s_1)\psi_{\downarrow}(s_2)+\psi_{\uparrow}(s_2)\psi_{\downarrow}(s_1)]=0 \nonumber \]
Since the wavefunction has a node midway between the two atoms, it is clearly antibonding and should have a higher energy than the corresponding bonding wavefunction \(\psi_g\).
A similar argument can be used for the molecule \(F_2\). Each \(F\) has an electronic configuration
\[1s^2 2s^2 2p_{x}^{2}2p_{y}^{2}2p_{z}^{1} \nonumber \]
and the Lewis structure of \(F_2\) is
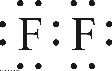
Most of the electrons are in lone pairs, but the \(2p_z\) electrons, which are unpaired in each \(F\) come together to form the bond. Thus, the bonding wavefunction should be a 2-electron wavefunction constructed from \(2p_z\) orbitals. The bonding wavefunction takes the "gerade" form as in \(H_2\):
\[\psi_g (r_1 ,r_2 ,s_1 ,s_2)=C_g [\psi_{2p_z}^{A}(r_1)\psi_{2p_z}^{B}(r_2)+\psi_{2p_z}^{A}(r_2)\psi_{2p_z}^{B}(r_1)][\psi_{\uparrow}(s_1)\psi_{\downarrow}(s_2)-\psi_{\uparrow}(s_2)\psi_{\downarrow}(s_1)] \nonumber \]
For \(HF\), the \(2p_z\) orbital on \(F\) and \(1s\) orbital on \(H\) come together to form the bonding wavefunction. To be consistent with the Pauli principle, we need a wavefunction of the form
\[\psi (r_1 ,r_2 ,s_1 ,s_2)=[\psi_{1s}^{H}(1)\psi_{2p_z}^{F}(2)+\psi_{1s}^{H}(2)\psi_{2p_z}^{F}(1)][\psi_{\uparrow}(s_1)\psi_{\downarrow}(s_2)-\psi_{\uparrow}(s_2)\psi_{\downarrow}(s_1)] \label{1}) \]
Looking at the \(HF\) example, it becomes clear how much valence bond theory attempts to appear as a "quantum version'' of the Lewis dot structure model. Valence bond theory attempts to construct very approximate wavefunctions for the bonding electrons in a Lewis structure, leaving the orbitals unused in the construction of the valence bond wavefunctions for the lone pair electrons. In the case of \(HF\), we use the \(2p_z\) orbitals of \(F\), which leaves the \(2s\), \(2p_x\) and \(2p_y\) orbitals unused. Since there are three lone pairs, these three orbitals are sufficient to hold each of the lone pairs as spin-up/spin-down couples.
Hybridization
For polyatomic molecules, the valence bond theory becomes a very poor approximation because the directionalities of the \(2s\) and \(2p\) orbitals is too restrictive to describe molecules with steric numbers ranging between 2 and 4. The example considered above of \(H_2 O\) illustrates this rather dramatically! Let us consider an even simpler molecule, \(BeH_2\), which has a steric number of 2 and is linear. Let the atoms lie entirely along the z-axis in the arrangement \(H-Be-H\).
Although \(Be\) has a ground-state electronic configuration of \(1s^2 2s^2\), but if we "promote" one of the \(2s\) electrons to a state with higher energy and allow its electronic structure to be \(1s^2 2s 2p_z\), then the unpaired electrons in the \(2s\) and \(2p_z\) orbitals can combine with the unpaired electrons in each of the hydrogen atoms to form bonds. The energy needed to excite the electron in Be would be ``repaid'' by the energy gained in the formation of stable bonds. The two valence-bond wavefunctions we would construct would be
\[\begin{align}\psi_1 (1,2) &= C_1 \left[\psi_{1s}^{H_1}(1)\psi_{2s}^{Be}(2)+\psi_{1s}^{H_1}(2)\psi_{2s}^{Be}(1) \right] \left[\psi_{\uparrow}(s_1)\psi_{\downarrow}(s_2)-\psi_{\uparrow}(s_2)\psi_{\downarrow}(s_1)\right]\\[4pt] \psi_2 (1,2) &= C_2 \left[\psi_{1s}^{H_2}(1)\psi_{2p_z}^{Be}(2)+\psi_{1s}^{H_2}(2)\psi_{2p_z}^{Be}(1)\right] \left[\psi_\uparrow (s_1)\psi_\downarrow (s_2)-\psi_\uparrow (s_2)\psi_\downarrow (s_1) \right]\end{align} \nonumber \]
Unfortunately, even this simple scheme does not work entirely because the two \(Be-H\) bonds would be different due to their construction from different combinations of orbitals. By symmetry, however, we can see that the two \(BeH\) bonds should be equivalent. A solution to this problem was proposed by Linus Pauling in the 30s in the form of orbital hybridization, a scheme that we still use today.
Pauling used the fact that in the first and second periods, the \(2s\) and \(2p\) orbitals have similar energies. Indeed, for \(H\), the energies are exactly the same. Given that these energies are not that different, we can combine s and p orbitals and still have a valid solution of the Schrödinger equation. That is, a general orbital
\[\chi (r)=C_1 \psi_{2s}(r)+C_2 \psi_{2p_x}(r)+C_3 \psi_{2p_y}(r)+C_4 \psi_{2p_z}(r) \nonumber \]
is also a solution of the Schrödinger equation with the same energy as a \(2s\) or \(2p\) orbitals individually (this is exactly true for \(H\)). In the case of \(BeH_2\), the external potential on the electrons in Be by the two hydrogens changes the energy levels and creates a near degeneracy between the \(2s\) and \(2p_z\) orbitals, hence, we are now free to combine the into linear combinations that are more suitable to the construction both of valence bond wavefunctions and MOs via the LCAO procedure.
\(sp\) Hybrid Orbitals
For Be, we now allow the s and p orbitals to mix and create two hybrid orbitals known as \(sp\) orbitals. The two new hybrid wavefunctions as linear combination of the functions for 2s and 2pz (using Dirac Notation):
\[| \chi_i \rangle = a_1|2s \rangle + b_1 |2p_z \rangle \label{sp1} \]
\[| \chi_j \rangle = a_2|2s \rangle + b_2 |2p_z \rangle \label{sp2} \]
These two wavefunctions must be orthogonal.
\[ \langle \chi_i | \chi_j \rangle = \delta_{ij} \nonumber \]
Which can be separated into the following relationships:
\[ \langle \chi_i | \chi_i \rangle = 1 \label{norm1} \]
and
\[\langle \chi_j | \chi_j \rangle = 1 \label{norm2} \]
and
\[ \langle \chi_i | \chi_j \rangle = \langle \chi_j | \chi_i \rangle = 0 \label{ortho} \]
Equations \(\ref{norm1}\) and \(\ref{norm2}\) are the normality requirement and Equation \(\ref{ortho}\) is the orthogonality requirement for the new hybrid wavefunctions. Substituting \(\ref{sp1}\) into \(\ref{norm1}\) results in
\[ \langle \chi_i | \chi_i \rangle = a_1^2 \cancelto{1}{\langle 2s | 2s \rangle } + a_1 b_1 \cancelto{0} {\langle 2s | 2p_z \rangle} + a_1 b_1 \cancelto{0} {\langle 2p_z | 2s} \rangle + b_1^2 \cancelto{1} {\langle 2p_z | 2p_z \rangle} =1 \nonumber \]
and similarly for \(\langle \chi_j | \chi_j \rangle\)
\[ \langle \chi_j | \chi_j \rangle = a_2^2 \cancelto{1}{\langle 2s | 2s \rangle } + a_2 b_2 \cancelto{0} {\langle 2s | 2p_z \rangle} + a_2 b_2 \cancelto{0} {\langle 2p_z | 2s} \rangle + b_2^2 \cancelto{1} {\langle 2p_z | 2p_z \rangle} =1 \nonumber \]
results in the following relationships
\[ \langle \chi_i | \chi_i \rangle = a_1^2 + b_1^2 = 1 \label{Con1} \]
\[ \langle \chi_j | \chi_j \rangle = a_2^2 + b_2^2 = 1 \label{Con2} \]
and
\[ \langle \chi_i | \chi_j \rangle = a_1a_2 + b_1b_2 = 0 \label{Con3} \]
These are four unknowns and three equations. The fourth "constraint" is that we assume contribution of \(|s\rangle\) is the same for both hybrid orbitals.
\[ a_1 = a_2 \nonumber \]
Equations \(\ref{Con1}\) to \(\ref{Con3}\) revert to
\[a_1^2 + b_1^2 = 1 \label{Con1a} \]
\[ a_1^2 + b_2^2 = 1 \label{Con2a} \]
\[ b_1^2 = b_2^2 \label{Con3a} \]
Therefore
\[ b_1 = -b_2 \nonumber \]
and
\[a_1 = b_1 \label{eq231} \]
Insert Equation \refPeq231} into \(\ref{Con3a}\) to get
\[a_1= \dfrac{1}{\sqrt{2}} \nonumber \]
and the two hybrid orbitals are
\[\begin{align}\chi_1 (r) &= \dfrac{1}{\sqrt{2}}[\psi_{2s}(r)+\psi_{2p_z}(r)]\\[4pt] \chi_2 (r) &= \dfrac{1}{\sqrt{2}}[\psi_{2s}(r)-\psi_{2p_z}(r)]\end{align} \nonumber \]
Note that these orbitals are both normalized and orthogonal:
\[\int |\chi_1 (r)|^2 dV=1 \ ; \ \int |\chi_2 (r)|^2 dV=1 \ ; \ \int \chi_{1}^{*}(r)\chi_2 (r)dV=0 \nonumber \]
These orbitals appear as shown in Figure 10.1.3
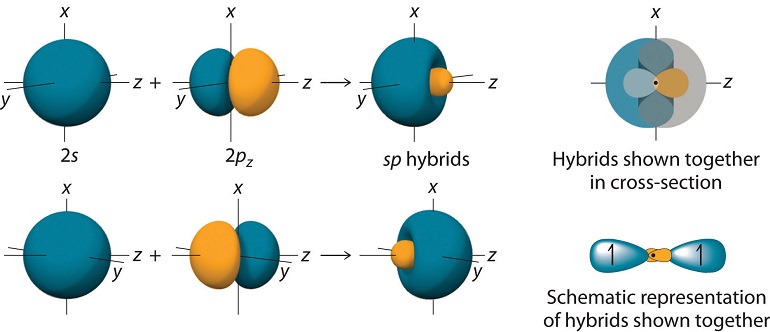
Given that the two \(sp\) hybrid orbitals are mirror images of each other, they can overlap with the \(1s\) orbital of \(H\) (shown in the figure) and create two equal bonds, as needed for \(BeH_2\). Using the valence bond formulation, now, one of the \(BeH\) bonds will be described by a wavefunction of the form:
\[\begin{align}\psi_1 (1,2) &= C_1 [\psi_{1s}^{H_1}(1)\chi_{1}^{Be}(2)+\psi_{1s}^{H_1}(2)\chi_{1}^{Be}(1)][\psi_{\uparrow}(s_1)\psi_{\downarrow}(s_2)-\psi_{\uparrow}(s_2)\psi_{\downarrow}(s_1)]\\[4pt] \psi_2 (1,2) &= C_2 [\psi_{1s}^{H_2}(1)\chi_{2}^{Be}(2)+\psi_{1s}^{H_2}(2)\chi_{2}^{Be}(1)][\psi_{\uparrow}(s_1)\psi_\downarrow (s_2)-\psi_{\uparrow}(s_2)\psi_\downarrow (s_1)]\end{align} \nonumber \]
In the above wavefunctions, it is clear that \(H_1\) is on the right and \(H_2\) is on the left, based on the directionalities of \(\chi_1\) and \(\chi_2\).
\(sp^2\) Hybrid Orbitals
For trigonal planar molecules such as \(BH_3\), we start with the electronic configuration of \(B\), which is \(1s^2 2s^2 2p_x\), and we promote one of the \(2s\) electrons to a \(2p_y\) orbital, so that we have \(1s^2 2s 2p_x 2p_y\). Suppose the geometry of \(BH_3\) is such that one of the hydrogens lies along the positive x axis. The remaining hydrogens would be in the 3rd and 4th quadrants, respectively, as shown in Figure 10.1.4 .
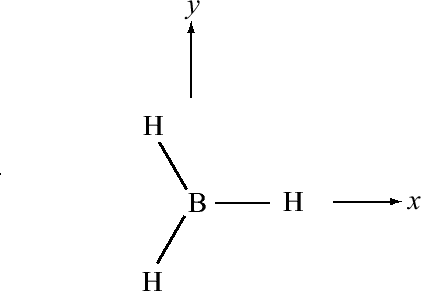
If we simply combine the \(2s\) with the \(2p_x\) and \(2p_y\) orbitals of boron, the resulting hybrid orbitals will not point in the correct direction. For this reason, we will create rotated versions of the \(p_x\) and \(p_y\) orbitals, which, as we will see are tantamount to taking new combinations of \(2p_x\) and \(2p_y\) orbitals to combine with the \(2s\). Since the rotation occurs in the \(xy\) plane, the coordinate that controls this is the azimuthal angle \(\phi\). For the \(p_x\) and \(p_y\) orbitals, the \(\phi\) dependence is
\[\psi_{2p_x}\sim \cos\phi \ ; \ \psi_{2p_y}\sim \sin\phi \nonumber \]
If we rotate \(2p_y\) by \(-30\) degrees (Figure 10.1.5 ; blue is positive and red is negative), the \(\phi\) dependence becomes
\[\psi_{2p_y}^{(rot)}\sim \sin(\phi +30) \nonumber \]
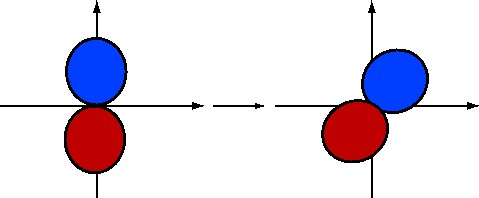
Using the fact that
\[\sin(\alpha \pm \beta)=\sin\alpha \cos\beta \pm cos\alpha sin\beta \nonumber \]
this rotation gives
\[\begin{align}\psi_{2p_y}^{(rot,1)} &\sim sin\phi \cos30+\cos\phi \sin30\\[4pt] &\sim \left [ \dfrac{\sqrt{3}}{2}\sin\phi +\dfrac{1}{2}\cos\phi \right ] \\[4pt] &\sim \left [ \dfrac{\sqrt{3}}{2}\psi_{2p_y}+\dfrac{1}{2}\psi_{2p_x}\right ]\end{align} \nonumber \]
Similarly, consider rotating \(-\psi_{2p_y}\) by \(+30\) degrees (Figure 10.1.6 ). This gives
\[\begin{align}-\psi_{2p_y}^{(rot,2)} &\sim -\sin(\phi -30)\\[4pt] &\sim -\left [ \dfrac{\sqrt{3}}{2}\sin\phi -\dfrac{1}{2}\cos\phi \right ] \\[4pt] &\sim -\dfrac{\sqrt{3}}{2}\psi_{2p_y}+\dfrac{1}{2}\psi_{2p_x}\end{align} \nonumber \]
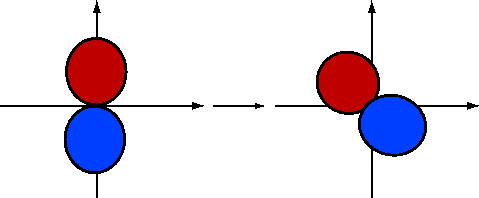
So, we now take the hybrid orbitals to be of the form
\[\begin{align}\chi_1 (r) &= a\psi_{2s}(r)-b\psi_{2p_x}\\[4pt] \chi_2 (r) &= c\psi_{2s}(r)+d\psi_{2p_y}^{(rot,1)}(r)\\[4pt] \chi_3 (r) &=c\psi_{2s}(r)-d\psi_{2p_y}^{(rot,2)}(r)\end{align} \nonumber \]
The coefficients \(a\), \(b\), and \(c\) are determined by requiring that the orbitals are normalized and mutually orthogonal:
\[\begin{align}\int |\chi_1 (r)|^2 dV=1 \ &; \ \int \chi_{1}^{*}(r)\chi_2 (r)dV=0\\[4pt] \int |\chi_2 (r)|^2 dV=1 \ &; \ \int \chi_{1}^{*}(r)\chi_3 (r)dV=0\\[4pt] \int |\chi_3 (r)|^2 dV=1 \ &; \ \int \chi_{2}^{*}(r)\chi_3 (r)dV=0\end{align} \nonumber \]
Carrying out the algebra, we obtain the following \(sp^2\) hybrid orbitals:
\[\begin{align}\chi_1 (r) &= \dfrac{1}{\sqrt{3}}[\psi_{2s}(r)-\sqrt{2}\psi_{2p_x}(r)]\\[4pt] \chi_2 (r) &= \dfrac{1}{\sqrt{6}}[\sqrt{2}\psi_{2s}(r)+\psi_{2p_x}(r)+\sqrt{3}\psi_{2p_y} (r)]\\[4pt] \chi_3 (r) &= \dfrac{1}{\sqrt{6}}[\sqrt{2}\psi_{2s}(r)+\psi_{2p_x}(r)-\sqrt{3}\psi_{2p_y}(r)]\end{align} \nonumber \]
The \(sp^2\) hybrids allow bonding at \(120^\circ\) degrees, and these orbitals appear as shown in Figure 10.1.7 :
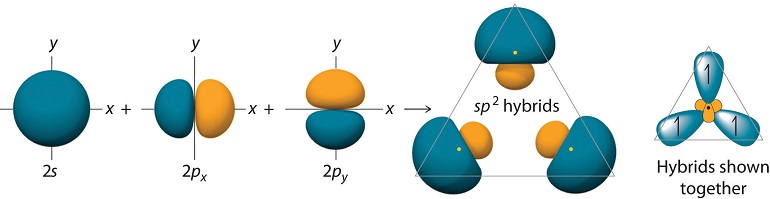
The figure also shows the overlaps of these orbitals with the \(1s\) orbitals of \(H\).
\(sp^3\) Hybrid Orbitals
Finally, we consider the case of methane \(CH_4\). The electronic configuration of \(C\) is \(1s^2 2s^2 2p_x 2p_y\). We now promote one of the \(2s\) orbitals to the \(2p_z\) orbital and write \(C\) as \(1s^2 2s2p_x 2p_y 2p_z\). We can now hybridize the \(2s\) orbital with each of the \(2p\) orbitals to create four hybrids:
\[\begin{align}\chi_1 (r) &= \dfrac{1}{2} \left[\psi_{2s}(r)+\psi_{2p_x}(r)+\psi_{2p_y}(r)+\psi_{2p_z}(r)\right]\\[4pt] \chi_2 (r) &= \dfrac{1}{2}\left[\psi_{2s}(r)-\psi_{2p_x}(r)-\psi_{2p_y}(r)+\psi_{2p_z}(r)\right]\\[4pt] \chi_3 (r) &= \dfrac{1}{2}\left[\psi_{2s}(r)+\psi_{2p_x}(r)-\psi_{2p_y}(r)-\psi_{2p_z}(r)\right]\\[4pt] \chi_4 (r) &= \dfrac{1}{2}\left[\psi_{2s}(r)-\psi_{2p_x}(r)+\psi_{2p_y}(r)-\psi_{2p_z}(r)\right]\end{align} \nonumber \]
The large lobes of the hybridized orbitals are oriented toward the vertices of a tetrahedron, with 109.5° angles between them (Figure 10.1.8 ). Like all the hybridized orbitals discussed earlier, the sp3 hybrid atomic orbitals are predicted to be equal in energy.
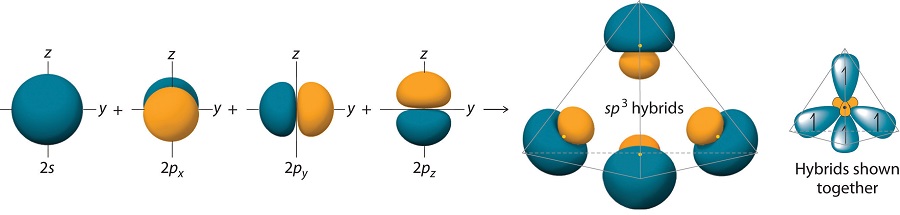
In addition to explaining why some elements form more bonds than would be expected based on their valence electron configurations, and why the bonds formed are equal in energy, valence bond theory explains why these compounds are so stable: the amount of energy released increases with the number of bonds formed. In the case of carbon, for example, much more energy is released in the formation of four bonds than two, so compounds of carbon with four bonds tend to be more stable than those with only two. Carbon does form compounds with only two covalent bonds (such as CH2 or CF2), but these species are highly reactive, unstable intermediates that form in only certain chemical reactions.
Hybridization is an often misconceived concept. It only is a mathematical interpretation, which explains a certain bonding situation (in an intuitive fashion). In a molecule the equilibrium geometry will result from various factors, such as steric and electronic interactions, and further more interactions with the surroundings like a solvent or external field. The geometric arrangement will not be formed because a molecule is hybridized in a certain way, it is the other way around, i.e. a result of the geometry or more precise and interpretation of the wavefunction for the given molecular arrangement.
The justification we gave for invoking hybridization in molecules such as BeH2, BF3 and CH4 was that the bonds in each are geometrically and chemically equivalent, whereas the atomic s- and p-orbitals on the central atoms are not. By combining these into new orbitals of sp, sp2 and sp3 types we obtain the required number of completely equivalent orbitals. This seemed easy enough to do on paper; we just drew little boxes and wrote “sp2” or whatever below them. But what is really going on here?
The full answer is beyond the scope of this course, so we can only offer the following very general explanation. First, recall what we mean by “orbital”: a mathematical function ψ having the character of a standing wave whose square ψ2 is proportional to the probability of finding the electron at any particular location in space. The latter, the electron density distribution, can be observed (by X-ray scattering, for example), and in this sense is the only thing that is “real”.
A given standing wave (ψ-function) can be synthesized by combining all kinds of fundamental wave patterns (that is, atomic orbitals) in much the same way that a color we observe can be reproduced by combining different sets of primary colors in various proportions. In neither case does it follow that these original orbitals (or colors) are actually present in the final product. So one could well argue that hybrid orbitals are not “real”; they simply turn out to be convenient for understanding the bonding of simple molecules at the elementary level, and this is why we use them.
Summary
The shape and bonding valecies of polyatomic molecules can be accounted for by hybrid orbitals. Molecular orbitals are formed from linear combinations of atomic orbitals which are similar in energy. These atomic orbitals could come from different atoms, or from the same atom. For example, the 2 sand 2patomic orbitals are very close energetically. When a linear combo of more than one atomic orbital from the same atom is formed, we have a hybrid orbital

