3.1.2.0: Atomic Orbitals and the Bohr Model (Problems)

PROBLEM \(\PageIndex{1}\)

Why is the electron in a Bohr hydrogen atom bound less tightly when it's electron is in energy level 3 than when it is in energy level 1?

Answer

An n of 3 indicated that the 1 electron in the hydrogen atom is in the third energy level, which is further from the nucleus than the first energy level (n=1), and therefore will not be as tightly bound.

PROBLEM \(\PageIndex{2}\)

The electron volt (eV) is a convenient unit of energy for expressing atomic-scale energies. It is the amount of energy that an electron gains when subjected to a potential of 1 volt; \(1 \;eV = 1.602 \times 10^{-19}\; J\). Using the Bohr model, determine the energy, in electron volts, of the photon produced when an electron in a hydrogen atom moves from the orbit with \(n = 5\) to the orbit with \(n = 2\).

Answer

2.856 eV

PROBLEM \(\PageIndex{3}\)

Using the Bohr model, determine the energy in joules of the photon produced when an electron in a \(\ce{He^{+}}\) ion moves from the orbit with n = 5 to the orbit with n = 2.

Answer

-4.58 × 10⁻¹⁹ J

Click here to see a video of the solution

PROBLEM \(\PageIndex{4}\)

Using the Bohr model, determine the energy in joules of the photon produced when an electron in a Li²⁺ ion moves from the orbit with n = 2 to the orbit with n = 1.

Answer

1.471 × 10⁻¹⁷ J

PROBLEM \(\PageIndex{5}\)

Consider a large number of hydrogen atoms with electrons randomly distributed in the n = 1, 2, 3, and 4 orbits

1. How many different wavelengths of light are emitted by these atoms as the electrons fall into lower-energy orbitals?
2. Calculate the lowest and highest energies of light produced by the transitions described in part (a).
3. Calculate the frequencies and wavelengths of the light produced by the transitions described in part (b).

Answer a

6 possible falls producing 6 wavelengths

Answer b

Highest: n=4 to n=1; -2.04 x 10^-18 J

Lowest: n=4 to n=3; -1.06 x 10^-19 J

Answer c

Highest: 9.73 x 10^-8 m; 3.08 x 10¹⁵ s^-1

Lowest: 1.87 x 10^-6 m; 1.60 x 10¹⁴ s^-1

Click here to see a video of the solution

PROBLEM \(\PageIndex{6}\)

The spectra of hydrogen and of calcium are shown below. What causes the lines in these spectra? Why are the colors of the lines different? Suggest a reason for the observation that the spectrum of calcium is more complicated than the spectrum of hydrogen.

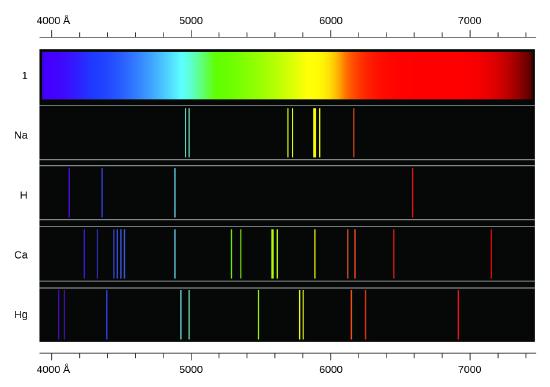
Answer

Both involve a relatively heavy nucleus with electrons moving around it, although strictly speaking, the Bohr model works only for one-electron atoms or ions. According to classical mechanics, the Rutherford model predicts a miniature “solar system” with electrons moving about the nucleus in circular or elliptical orbits that are confined to planes. If the requirements of classical electromagnetic theory that electrons in such orbits would emit electromagnetic radiation are ignored, such atoms would be stable, having constant energy and angular momentum, but would not emit any visible light (contrary to observation). If classical electromagnetic theory is applied, then the Rutherford atom would emit electromagnetic radiation of continually increasing frequency (contrary to the observed discrete spectra), thereby losing energy until the atom collapsed in an absurdly short time (contrary to the observed long-term stability of atoms). The Bohr model retains the classical mechanics view of circular orbits confined to planes having constant energy and angular momentum, but restricts these to quantized values dependent on a single quantum number, n. The orbiting electron in Bohr’s model is assumed not to emit any electromagnetic radiation while moving about the nucleus in its stationary orbits, but the atom can emit or absorb electromagnetic radiation when the electron changes from one orbit to another. Because of the quantized orbits, such “quantum jumps” will produce discrete spectra, in agreement with observations.

PROBLEM \(\PageIndex{7}\)

How are the Bohr model and the quantum mechanical model of the hydrogen atom similar? How are they different?

Answer

Both models have a central positively charged nucleus with electrons moving about the nucleus in accordance with the Coulomb electrostatic potential. The Bohr model assumes that the electrons move in circular orbits that have quantized energies, angular momentum, and radii that are specified by a single quantum number, n = 1, 2, 3, …, but this quantization is an ad hoc assumption made by Bohr to incorporate quantization into an essentially classical mechanics description of the atom. Bohr also assumed that electrons orbiting the nucleus normally do not emit or absorb electromagnetic radiation, but do so when the electron switches to a different orbit. In the quantum mechanical model, the electrons do not move in precise orbits (such orbits violate the Heisenberg uncertainty principle) and, instead, a probabilistic interpretation of the electron’s position at any given instant is used, with a mathematical function ψ called a wavefunction that can be used to determine the electron’s spatial probability distribution. These wavefunctions, or orbitals, are three-dimensional stationary waves that can be specified by three quantum numbers that arise naturally from their underlying mathematics (no ad hoc assumptions required): the principal quantum number, n (the same one used by Bohr), which specifies shells such that orbitals having the same n all have the same energy and approximately the same spatial extent; the angular momentum quantum number l, which is a measure of the orbital’s angular momentum and corresponds to the orbitals’ general shapes, as well as specifying subshells such that orbitals having the same l (and n) all have the same energy; and the orientation quantum number m, which is a measure of the z component of the angular momentum and corresponds to the orientations of the orbitals. The Bohr model gives the same expression for the energy as the quantum mechanical expression and, hence, both properly account for hydrogen’s discrete spectrum (an example of getting the right answers for the wrong reasons, something that many chemistry students can sympathize with), but gives the wrong expression for the angular momentum (Bohr orbits necessarily all have non-zero angular momentum, but some quantum orbitals [s orbitals] can have zero angular momentum).

Have a video solution request?

Let your professors know here.

***Please know that you are helping future students - videos will be made in time for next term's class.

Contributors and Attributions

• Paul Flowers (University of North Carolina - Pembroke), Klaus Theopold (University of Delaware) and Richard Langley (Stephen F. Austin State University) with contributing authors. Textbook content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at http://cnx.org/contents/85abf193-2bd...a7ac8df6@9.110).

• Adelaide Clark, Oregon Institute of Technology

Feedback

Think one of the answers above is wrong? Let us know here.