Another interesting consequence of lattice energies involves the formation of certain salts containing Na- and e- anions. These compounds are known as alkalides and electrides, respectively.[9] Most of these compounds have been discovered by Prof. James Dye at Michigan State University.
The alkali metals have one electron in their valence shell. For example, the electronic configurations of Na and K are [Ar]3s1 and [Kr]4s1, respectively. Although we are accustomed to seeing these very electropositive elements give up their electrons when they make compounds with electronegative elements, they can also gain an electron to achieve a [noble gas]ns2 configuration. This is possible with strong electron donors such as alkali metals, especially when the cation that is formed is stabilized by coordination to a crown ether. Typically, these compounds are synthesized by combining the alkali metal and the appropriate crown ether in liquid ammonia, and then evaporating the ammonia.
|

Cavities and channels in an electride
|
Electride salts are formed under similar conditions, except in this case the anion is simply an electron that exists in an anion "cavity" in the crystal. The crystal structures are clearly salt-like, with the cations (alkali cations stabilized by crown or cryptand ligands) alternating in the structure with electrons.
Alkalide Salt
\[\ce{2Na ->[NH_{3}] Na^{+}(NH3)+ e^{-}(NH3) ->[18C6] [Na(18C6)]^{+} Na^{-}}\]
Electride Salt
\[\ce{2Cs ->[NH_{3}][18C6] [Cs(18C6)]^{+} e^{-}}\]
Complexing Na+ (K+, Rb+, Cs+) with crown ether ligands stabilizes the M+ form of the metal ("salt" form). Because the metal cation with its ligand shell is rather large, the lattice energy of these salts is rather low.
|
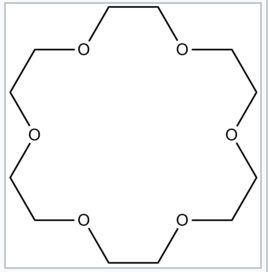
18-Crown-6, a crown ether that strongly complexes Na+ cations
|
Solutions of electride salts are powerful reducing agents, as demonstrated by their use in the Birch reduction, in which aromatic compounds are hydrogenated to produce dienes. Electrides are also useful for reducing metal ions to metals. Evaporation of blue electride solutions in anhydrous ammonia affords a mirror of Na. Such solutions slowly lose their color as the electrons reduce ammonia to the amide anion:
\(\ce{[Na(NH3)6]^{+}e^{-} + NH3 -> NaNH2 + H2}\)
It is interesting to consider, in the context of lattice energies and Born-Haber cycles, what might happen without these ligands present. That is, we can ask the question of whether sodium metal would prefer to exist in the metallic form as Na(s), or to form the sodide salt Na+Na-, or the electride salt Na+ e-. Of course, we already know the answer to this question. Elemental sodium is clearly a metal (it is shiny, conducts electricity, and has a bcc crystal structure) and has never been observed in either of the "salt" forms. But how far away are these forms energetically?
We can calculate the energetics by assuming that the Na- ion is about the same size as Br-, and that the e- anion is about the same size as Cl-. Then the lattice energies in the cycles become the same as those of NaBr and NaCl:
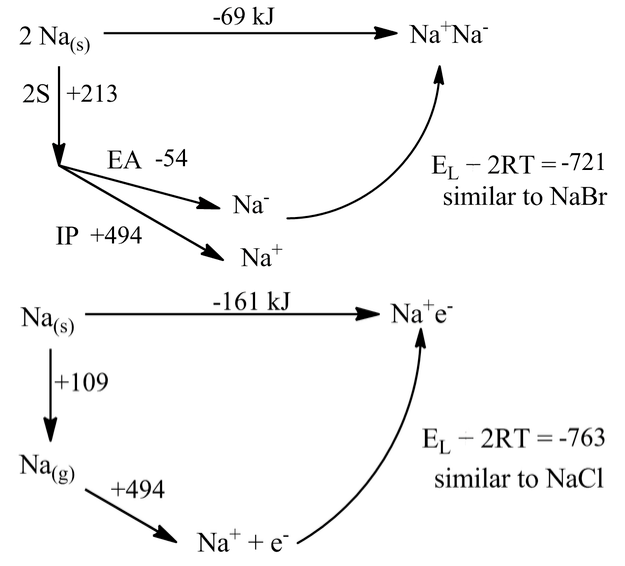
The rather surprising result from these calculations is that sodium would be marginally stable as a sodide salt and very stable (by 161 kJ) as an electride. All the terms in these simple cycles are known precisely. But we must be doing something wrong here, because Na(s) is clearly metallic.
The key, subtle point here is that Born-Haber cycles consider only the potential energy (rather than the total energy) of the substances in the cycle. Normally we can ignore the kinetic energy part of the total energy, but in this case we cannot because of the quantum mechanical effect of resonance.




