The Mass Spectra of Elements

This page looks at the information you can get from the mass spectrum of an element. It shows how you can find out the masses and relative abundances of the various isotopes of the element and use that information to calculate the relative atomic mass of the element. It also looks at the problems thrown up by elements with diatomic molecules - like chlorine, Cl₂.

The mass spectrum of monatomic elements

Monatomic elements include all those except for things like chlorine, Cl₂, with molecules containing more than one atom.

Example \(\PageIndex{1}\):  The Mass Spectrum of Boron

The number of isotopes: The two peaks in the mass spectrum shows that there are 2 isotopes of boron - with relative isotopic masses of 10 and 11 on the ¹²C scale.

The abundance of the isotopes: The relative sizes of the peaks gives you a direct measure of the relative abundances of the isotopes. The tallest peak is often given an arbitrary height of 100 - but you may find all sorts of other scales used. It doesn't matter in the least. You can find the relative abundances by measuring the lines on the stick diagram. In this case, the two isotopes (with their relative abundances) are:

boron-10		23
boron-11		100

Working out the relative atomic mass

The relative atomic mass (RAM) of an element is given the symbol A_r and is defined as:

The relative atomic mass of an element is the weighted average of the masses of the isotopes on a scale on which a carbon-12 atom has a mass of exactly 12 units A "weighted average" allows for the fact that there won't be equal amounts of the various isotopes. The example coming up should make that clear.

Suppose you had 123 typical atoms of boron. 23 of these would be ¹⁰B and 100 would be ¹¹B.

The total mass of these would be (23 x 10) + (100 x 11) = 1330

The average mass of these 123 atoms would be 1330 / 123 = 10.8 (to 3 significant figures).

10.8 is the relative atomic mass of boron.

Notice the effect of the "weighted" average. A simple average of 10 and 11 is, of course, 10.5. Our answer of 10.8 allows for the fact that there are a lot more of the heavier isotope of boron - and so the "weighted" average ought to be closer to that.

Example \(\PageIndex{2}\): The Mass Spectrum of Zirconium

 

The number of isotopes: The 5 peaks in the mass spectrum shows that there are 5 isotopes of zirconium - with relative isotopic masses of 90, 91, 92, 94 and 96 on the ¹²C scale.

The abundance of the isotopes: This time, the relative abundances are given as percentages. Again you can find these relative abundances by measuring the lines on the stick diagram. In this case, the 5 isotopes (with their relative percentage abundances) are:

zirconium-90		51.5
zirconium-91		11.2
zirconium-92		17.1
zirconium-94		17.4
zirconium-96		2.8

 

Working out the relative atomic mass

Suppose you had 100 typical atoms of zirconium. 51.5 of these would be ⁹⁰Zr, 11.2 would be ⁹¹Zr and so on.

The total mass of these 100 typical atoms would be

(51.5 x 90) + (11.2 x 91) + (17.1 x 92) + (17.4 x 94) + (2.8 x 96) = 9131.8

The average mass of these 100 atoms would be 9131.8 / 100 = 91.3 (to 3 significant figures). 91.3 is the relative atomic mass of zirconium.

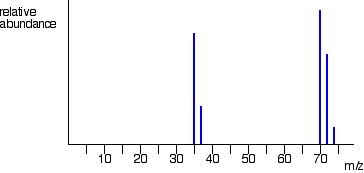
Example \(\PageIndex{3}\): The Mass Spectrum of Chlorine

Chlorine is taken as typical of elements with more than one atom per molecule. We'll look at its mass spectrum to show the sort of problems involved. Chlorine has two isotopes, ³⁵Cl and ³⁷Cl, in the approximate ratio of 3 atoms of ³⁵Cl to 1 atom of ³⁷Cl. You might suppose that the mass spectrum would look like this:

 

You would be wrong! The problem is that chlorine consists of molecules, not individual atoms. When chlorine is passed into the ionization chamber, an electron is knocked off the molecule to give a molecular ion, Cl₂⁺. These ions won't be particularly stable, and some will fall apart to give a chlorine atom and a Cl⁺ ion. The term for this is fragmentation.

\[\ce{ Cl_2^{+} \rightarrow Cl + Cl^{+}}\]

If the Cl atom formed is not then ionized in the ionization chamber, it simply gets lost in the machine - neither accelerated nor deflected.

The Cl⁺ ions will pass through the machine and will give lines at 35 and 37, depending on the isotope and you would get exactly the pattern in the last diagram. The problem is that you will also record lines for the unfragmented Cl₂⁺ ions.

Think about the possible combinations of chlorine-35 and chlorine-37 atoms in a Cl₂⁺ ion. Both atoms could be ³⁵Cl, both atoms could be ³⁷Cl, or you could have one of each sort. That would give you total masses of the Cl₂⁺ ion of:

 

35 + 35 = 70

35 + 37 = 72

37 + 37 = 74

That means that you would get a set of lines in the m/z = 70 region looking like this:

 

 

These lines would be in addition to the lines at 35 and 37.

The relative heights of the 70, 72 and 74 lines are in the ratio 9:6:1. If you know the right bit of math, it's very easy to show this. If not, don't worry. Just remember that the ratio is 9:6:1.

What you can't do is make any predictions about the relative heights of the lines at 35/37 compared with those at 70/72/74. That depends on what proportion of the molecular ions break up into fragments. That's why you've got the chlorine mass spectrum in two separate bits so far. You must realise that the vertical scale in the diagrams of the two parts of the spectrum isn't the same.

The overall mass spectrum looks like this:

 

Contributors

• Jim Clark (Chemguide.co.uk)