14.1: Optimizing the Experimental Procedure
- Page ID
- 220782
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)In the presence of H2O2 and H2SO4, a solution of vanadium forms a reddish brown color that is believed to be a compound with the general formula (VO)2(SO4)3. The intensity of the solution’s color depends on the concentration of vanadium, which means we can use its absorbance at a wavelength of 450 nm to develop a quantitative method for vanadium.
The intensity of the solution’s color also depends on the amounts of H2O2 and H2SO4 that we add to the sample—in particular, a large excess of H2O2 decreases the solution’s absorbance as it changes from a reddish brown color to a yellowish color [Vogel’s Textbook of Quantitative Inorganic Analysis, Longman: London, 1978, p. 752.]. Developing a standard method for vanadium based on this reaction requires that we optimize the amount of H2O2 and H2SO4 added to maximize the absorbance at 450 nm. Using the terminology of statisticians, we call the solution’s absorbance the system’s response. Hydrogen peroxide and sulfuric acid are factors whose concentrations, or factor levels, determine the system’s response. To optimize the method we need to find the best combination of factor levels. Usually we seek a maximum response, as is the case for the quantitative analysis of vanadium as (VO)2(SO4)3. In other situations, such as minimizing an analysis’s percent error, we seek a minimum response.
We will return to this analytical method for vanadium in Example \(\PageIndex{4}\) and Problem 11 from the end-of-chapter problems.
Response Surfaces
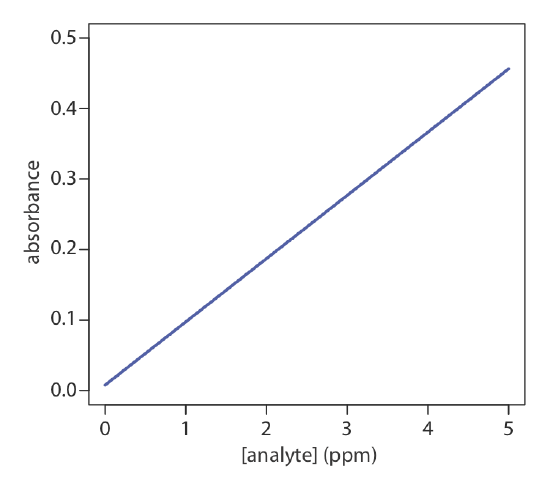
One of the most effective ways to think about an optimization is to visualize how a system’s response changes when we increase or decrease the levels of one or more of its factors. We call a plot of the system’s response as a function of the factor levels a response surface. The simplest response surface has one factor and is drawn in two dimensions by placing the responses on the y-axis and the factor’s levels on the x-axis. The calibration curve in Figure \(\PageIndex{1}\) is an example of a one-factor response surface. We also can define the response surface mathematically. The response surface in Figure \(\PageIndex{1}\), for example, is
\[A = 0.008 + 0.0896C_A \nonumber\]
where A is the absorbance and CA is the analyte’s concentration in ppm.
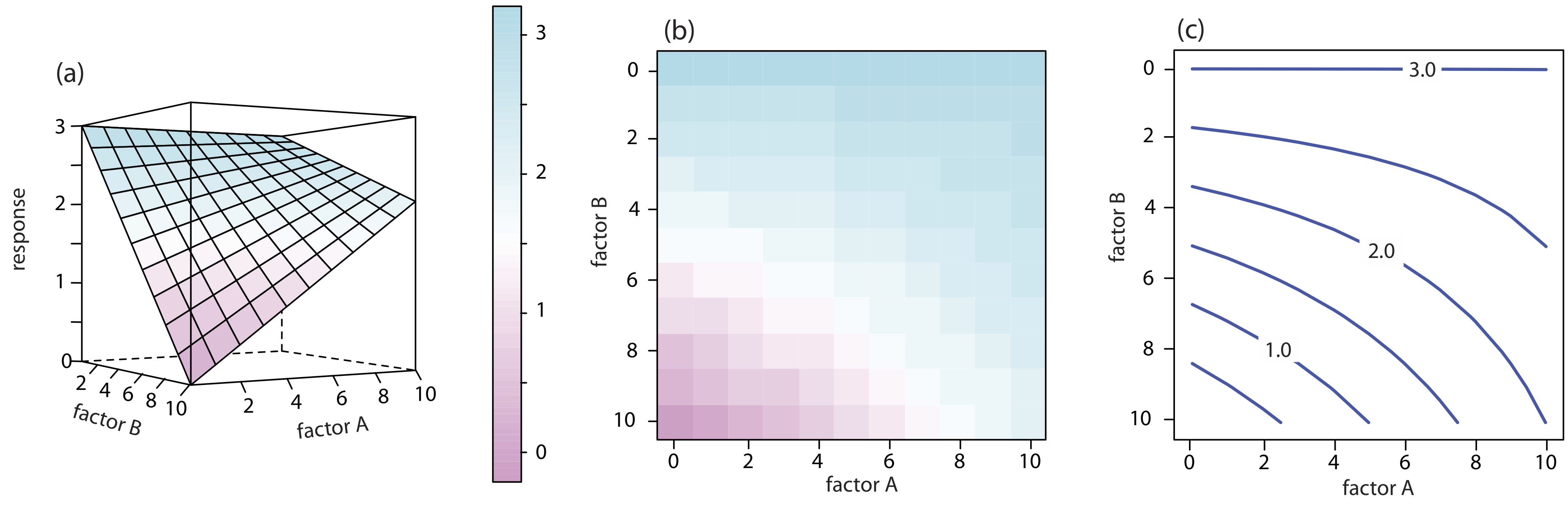
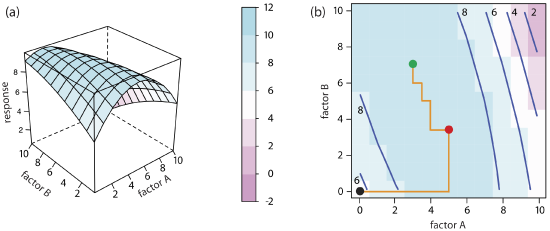
For a two-factor system, such as the quantitative analysis for vanadium described earlier, the response surface is a flat or curved plane in three dimensions. As shown in Figure \(\PageIndex{2}\)a, we place the response on the z-axis and the factor levels on the x-axis and the y-axis. Figure \(\PageIndex{2}\)a shows a pseudo-three dimensional wireframe plot for a system that obeys the equation
\[R = 3.0 - 0.30A + 0.020AB \nonumber\]
where R is the response, and A and B are the factors. We also can represent a two-factor response surface using the two-dimensional level plot in Figure \(\PageIndex{2}\)b, which uses a color gradient to show the response on a two-dimensional grid, or using the two-dimensional contour plot in Figure \(\PageIndex{2}\)c, which uses contour lines to display the response surface.
We also can overlay a level plot and a contour plot. See Figure \(\PageIndex{7}\)b for a typical example.
The response surfaces in Figure \(\PageIndex{2}\) cover a limited range of factor levels (0 ≤ A ≤ 10, 0 ≤ B ≤ 10), but we can extend each to more positive or to more negative values because there are no constraints on the factors. Most response surfaces of interest to an analytical chemist have natural constraints imposed by the factors, or have practical limits set by the analyst. The response surface in Figure \(\PageIndex{1}\), for example, has a natural constraint on its factor because the analyte’s concentration cannot be less than zero.
We express this constraint as CA ≥ 0.
If we have an equation for the response surface, then it is relatively easy to find the optimum response. Unfortunately, when developing a new analytical method, we rarely know any useful details about the response surface. Instead, we must determine the response surface’s shape and locate its optimum response by running appropriate experiments. The focus of this section is on useful experimental methods for characterizing a response surface. These experimental methods are divided into two broad categories: searching methods, in which an algorithm guides a systematic search for the optimum response, and modeling methods, in which we use a theoretical model or an empirical model of the response surface to predict the optimum response.
Searching Algorithms for Response Surfaces
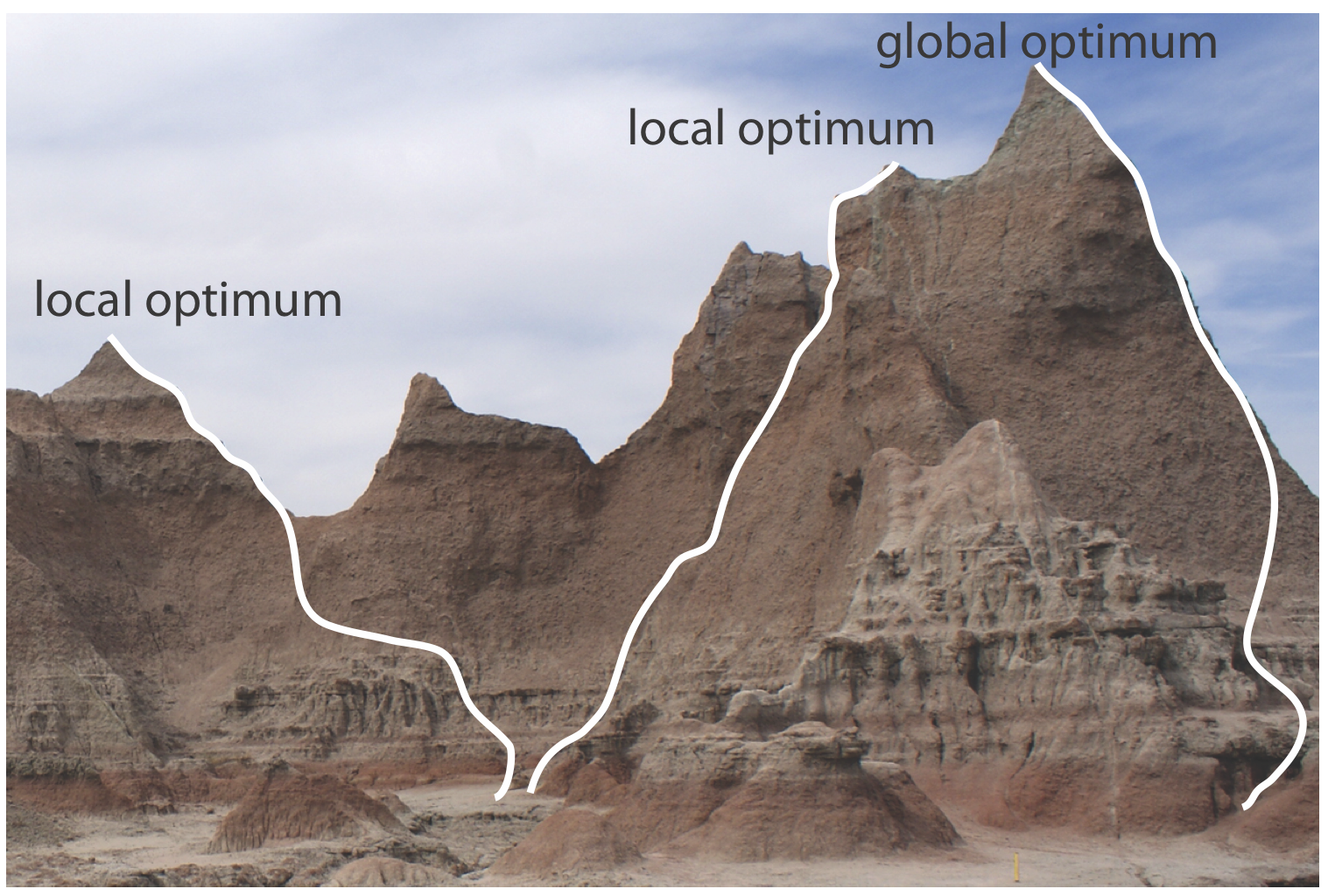
Figure \(\PageIndex{3}\) shows a portion of the South Dakota Badlands, a barren landscape that includes many narrow ridges formed through erosion. Suppose you wish to climb to the highest point on this ridge. Because the shortest path to the summit is not obvious, you might adopt the following simple rule: look around you and take one step in the direction that has the greatest change in elevation, and then repeat until no further step is possible. The route you follow is the result of a systematic search that uses a searching algorithm. Of course there are as many possible routes as there are starting points, three examples of which are shown in Figure \(\PageIndex{3}\). Note that some routes do not reach the highest point—what we call the global optimum. Instead, many routes reach a local optimum from which further movement is impossible.
We can use a systematic searching algorithm to locate the optimum response for an analytical method. We begin by selecting an initial set of factor levels and measure the response. Next, we apply the rules of our searching algorithm to determine a new set of factor levels and measure its response, continuing this process until we reach an optimum response. Before we consider two common searching algorithms, let’s consider how we evaluate a searching algorithm.
Effectiveness and Efficiency
A searching algorithm is characterized by its effectiveness and its efficiency. To be effective, a searching algorithm must find the response surface’s global optimum, or at least reach a point near the global optimum. A searching algorithm may fail to find the global optimum for several reasons, including a poorly designed algorithm, uncertainty in measuring the response, and the presence of local optima. Let’s consider each of these potential problems.
A poorly designed algorithm may prematurely end the search before it reaches the response surface’s global optimum. As shown in Figure \(\PageIndex{4}\), when climbing a ridge that slopes up to the northeast, an algorithm is likely to fail it if limits your steps only to the north, south, east, or west. An algorithm that cannot responds to a change in the direction of steepest ascent is not an effective algorithm.
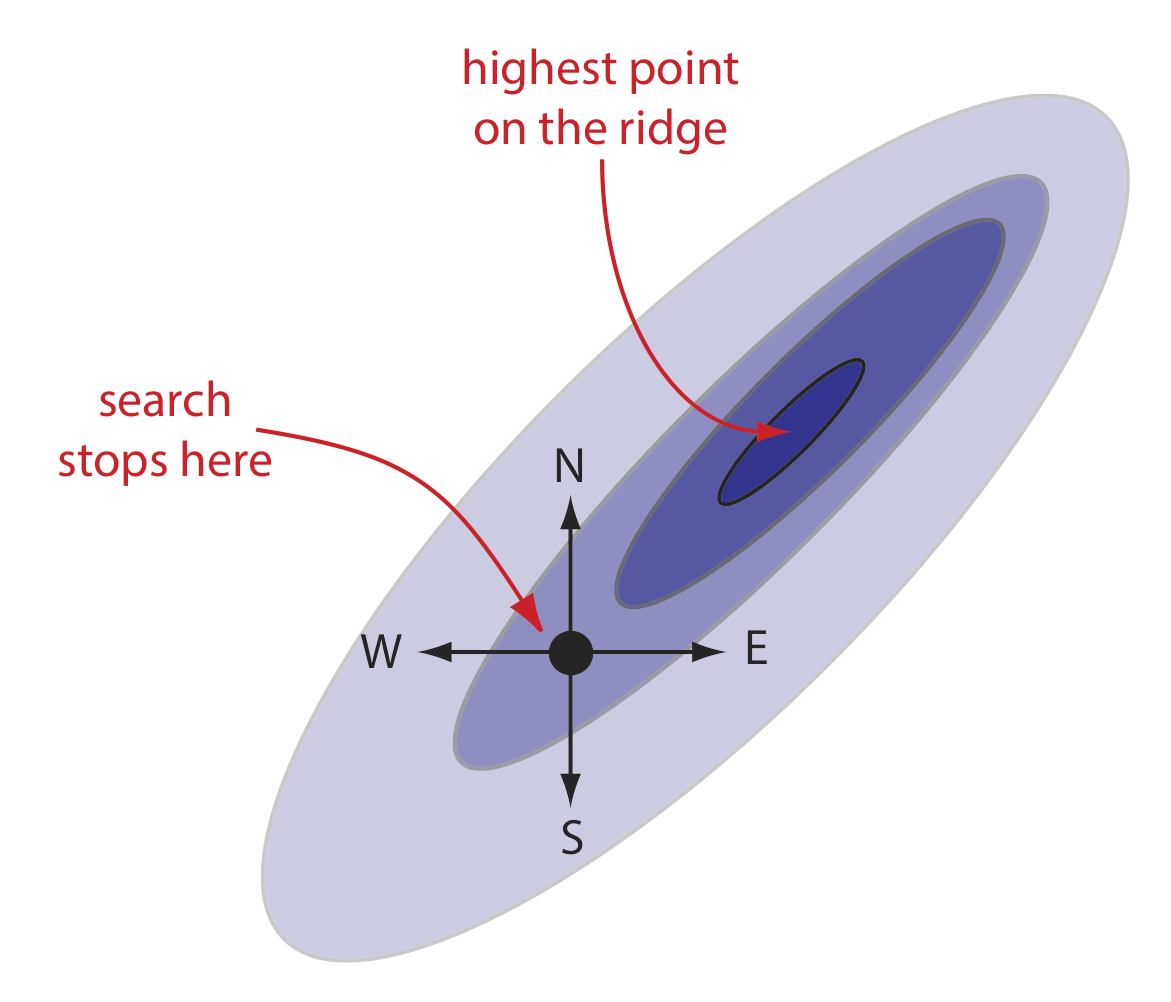
All measurements contain uncertainty, or noise, that affects our ability to characterize the underlying signal. When the noise is greater than the local change in the signal, then a searching algorithm is likely to end before it reaches the global optimum. Figure \(\PageIndex{5}\) provides a different view of Figure \(\PageIndex{3}\), which shows us that the relatively flat terrain leading up to the ridge is heavily weathered and very uneven. Because the variation in local height (the noise) exceeds the slope (the signal), our searching algorithm ends the first time we step up onto a less weathered local surface.

Finally, a response surface may contain several local optima, only one of which is the global optimum. If we begin the search near a local optimum, our searching algorithm may never reach the global optimum. The ridge in Figure \(\PageIndex{3}\), for example, has many peaks. Only those searches that begin at the far right will reach the highest point on the ridge. Ideally, a searching algorithm should reach the global optimum regardless of where it starts.
A searching algorithm always reaches an optimum. Our problem, of course, is that we do not know if it is the global optimum. One method for evaluating a searching algorithm’s effectiveness is to use several sets of initial factor levels, find the optimum response for each, and compare the results. If we arrive at or near the same optimum response after starting from very different locations on the response surface, then we are more confident that is it the global optimum.
Efficiency is a searching algorithm’s second desirable characteristic. An efficient algorithm moves from the initial set of factor levels to the optimum response in as few steps as possible. In seeking the highest point on the ridge in Figure \(\PageIndex{5}\), we can increase the rate at which we approach the optimum by taking larger steps. If the step size is too large, however, the difference between the experimental optimum and the true optimum may be unacceptably large. One solution is to adjust the step size during the search, using larger steps at the beginning and smaller steps as we approach the global optimum.
One-Factor-at-a-Time Optimization
A simple algorithm for optimizing the quantitative method for vanadium described earlier is to select initial concentrations for H2O2 and H2SO4 and measure the absorbance. Next, we optimize one reagent by increasing or decreasing its concentration—holding constant the second reagent’s concentration—until the absorbance decreases. We then vary the concentration of the second reagent—maintaining the first reagent’s optimum concentration—until we no longer see an increase in the absorbance. We can stop this process, which we call a one-factor-at-a-time optimization, after one cycle or repeat the steps until the absorbance reaches a maximum value or it exceeds an acceptable threshold value.
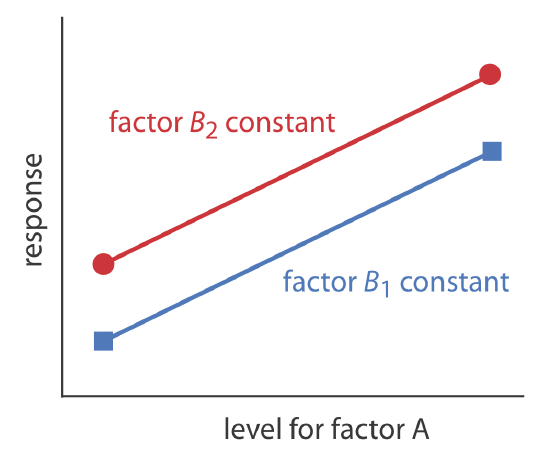
A one-factor-at-a-time optimization is consistent with a notion that to determine the influence of one factor we must hold constant all other factors. This is an effective, although not necessarily an efficient experimental design when the factors are independent [Sharaf, M. A.; Illman, D. L.; Kowalski, B. R. Chemometrics, Wiley-Interscience: New York, 1986]. Two factors are independent when a change in the level of one factor does not influence the effect of a change in the other factor’s level. Table \(\PageIndex{1}\) provides an example of two independent factors.
| factor A | factor B | response |
|---|---|---|
| \(A_1\) | \(B_1\) | 40 |
| \(A_2\) | \(B_1\) | 80 |
| \(A_1\) | \(B_2\) | 60 |
| \(A_2\) | \(B_2\) | 100 |
If we hold factor B at level B1, changing factor A from level A1 to level A2 increases the response from 40 to 80, or a change in response, \(\Delta R\) of
\[R = 80 - 40 = 40 \nonumber\]
If we hold factor B at level B2, we find that we have the same change in response when the level of factor A changes from A1 to A2.
\[R = 100 - 60 = 40 \nonumber\]
We can see this independence visually if we plot the response as a function of factor A’s level, as shown in Figure \(\PageIndex{6}\). The parallel lines show that the level of factor B does not influence factor A’s effect on the response.
Using the data in Table \(\PageIndex{1}\), show that the effect of factor B on the response is independent of factor A.
- Answer
-
If we hold factor A at level A1, changing factor B from level B1 to level B2 increases the response from 40 to 60, or a change, \(\Delta R\), of
\[\Delta R = 60 - 40 = 20 \nonumber\]
If we hold factor A at level A2, we find that we have the same change in response when the level of factor B changes from B1 to B2.
\[\Delta R = 100 - 80 = 20 \nonumber\]
Mathematically, two factors are independent if they do not appear in the same term in the equation that describes the response surface. Equation \(\PageIndex{1}\), for example, describes a response surface with independent factors because no term in the equation includes both factor A and factor B.
\[R = 2.0 + 0.12 A + 0.48 B - 0.03A^2 - 0.03 B^2 \label{14.1}\]
Figure \(\PageIndex{7}\) shows the resulting pseudo-three-dimensional surface and a contour map for equation \ref{14.1}.
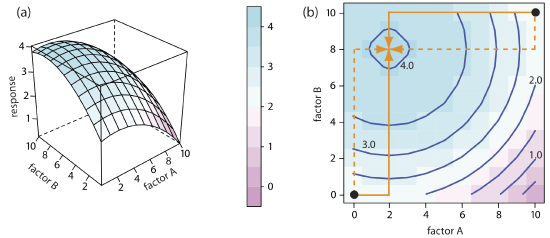
The easiest way to follow the progress of a searching algorithm is to map its path on a contour plot of the response surface. Positions on the response surface are identified as (a, b) where a and b are the levels for factor A and for factor B. The contour plot in Figure \(\PageIndex{7}\)b, for example, shows four one-factor-at-a-time optimizations of the response surface for equation \ref{14.1}. The effectiveness and efficiency of this algorithm when optimizing independent factors is clear—each trial reaches the optimum response at (2, 8) in a single cycle.
Unfortunately, factors often are not independent. Consider, for example, the data in Table \(\PageIndex{2}\)
| factor A | factor B | response |
|---|---|---|
| \(A_1\) | \(B_1\) | 20 |
| \(A_2\) | \(B_1\) | 80 |
| \(A_1\) | \(B_2\) | 60 |
| \(A_2\) | \(B_2\) | 80 |
where a change in the level of factor B from level B1 to level B2 has a significant effect on the response when factor A is at level A1
\[R = 60 - 20 = 40 \nonumber\]
but no effect when factor A is at level A2.
\[R = 80 - 80 = 0 \nonumber\]
Figure \(\PageIndex{8}\) shows this dependent relationship between the two factors. Factors that are dependent are said to interact and the equation for the response surface’ includes an interaction term that contains both factor A and factor B. The final term in equation \(\PageIndex{2}\), for example, accounts for the interaction between factor A and factor B.
\[R = 5.5 + 1.5 A + 0.6 B - 0.15 A^2 - 0.245 B^2 - 0.0857 AB \label{14.2}\]
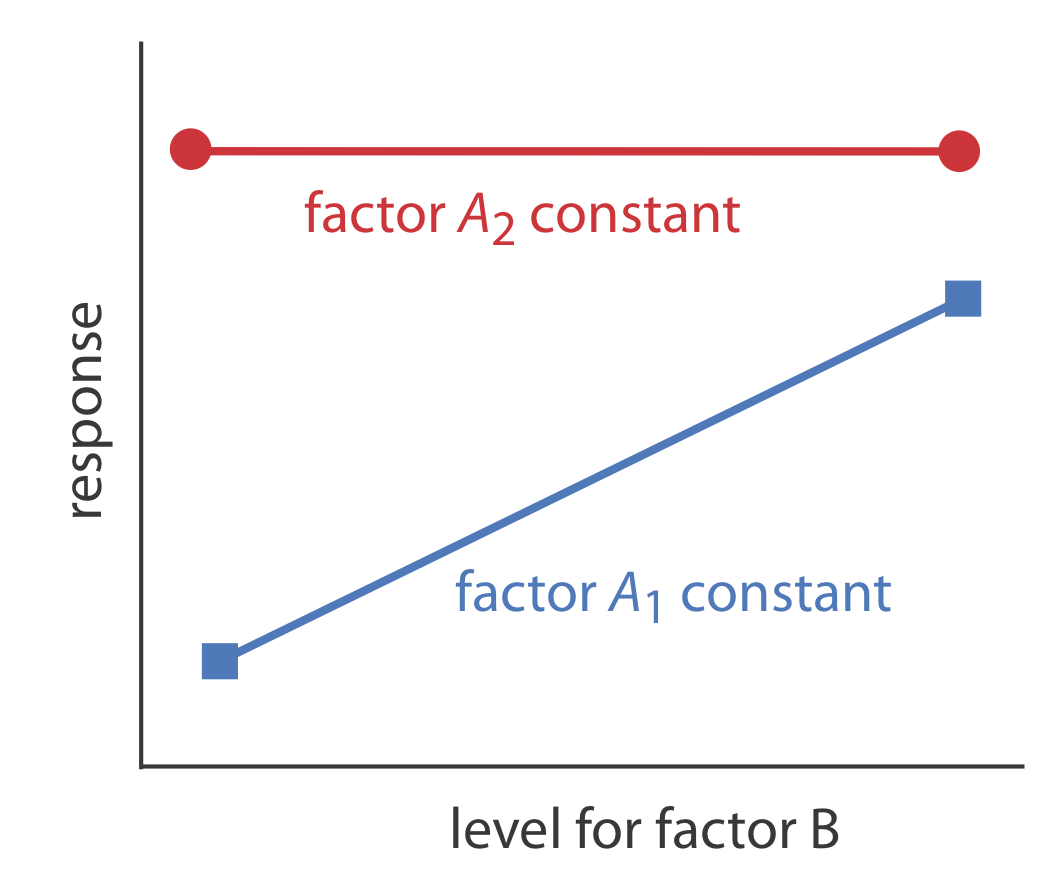
Figure \(\PageIndex{9}\) shows the resulting pseudo-three-dimensional surface and a contour map for equation \ref{14.2}.
Using the data in Table \(\PageIndex{2}\), show that the effect of factor A on the response is independent of factor B.
- Answer
-
If we hold factor B at level B1, changing factor A from level A1 to level A2 increases the response from 20 to 80, or a change, \(\Delta R\), of
\[\Delta R = 80 - 20 = 60 \nonumber\]
If we hold factor B at level B2, we find that the change in response when the level of factor A changes from A1 to A2 is now 20.
\[\Delta R = 80 - 60 = 20 \nonumber\]
The progress of a one-factor-at-a-time optimization for equation \ref{14.2} is shown in Figure \(\PageIndex{9}\)b. Although the optimization for dependent factors is effective, it is less efficient than that for independent factors. In this case it takes four cycles to reach the optimum response of (3, 7) if we begin at (0, 0).
Simplex Optimization
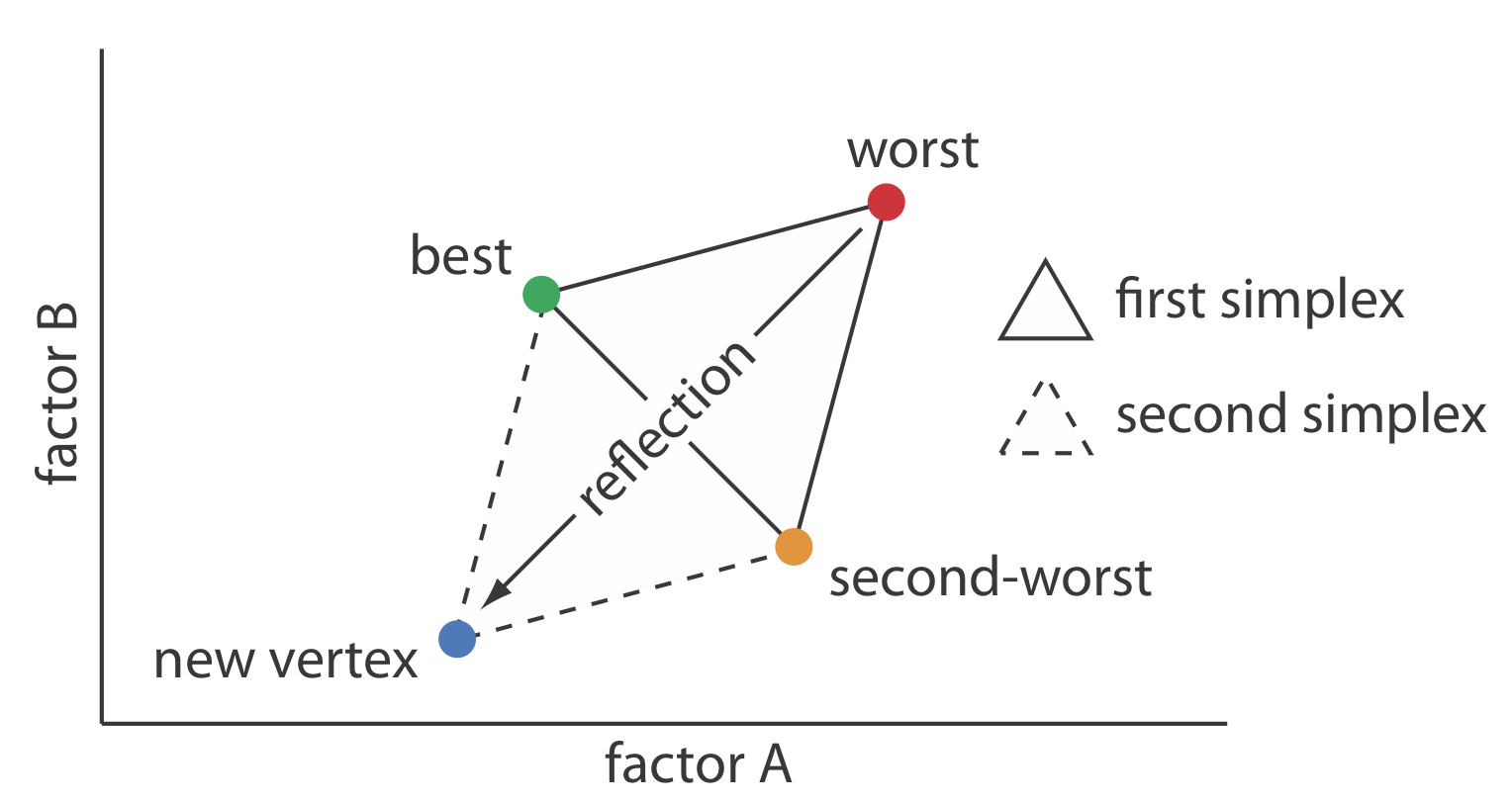
One strategy for improving the efficiency of a searching algorithm is to change more than one factor at a time. A convenient way to accomplish this when there are two factors is to begin with three sets of initial factor levels as the vertices of a triangle. After measuring the response for each set of factor levels, we identify the combination that gives the worst response and replace it with a new set of factor levels using a set of rules (Figure \(\PageIndex{10}\)). This process continues until we reach the global optimum or until no further optimization is possible. The set of factor levels is called a simplex. In general, for k factors a simplex is a \(k + 1\) dimensional geometric figure [(a) Spendley, W.; Hext, G. R.; Himsworth, F. R. Technometrics 1962, 4, 441–461; (b) Deming, S. N.; Parker, L. R. CRC Crit. Rev. Anal. Chem. 1978 7(3), 187–202].
Thus, for two factors the simplex is a triangle. For three factors the simplex is a tetrahedron.
To place the initial two-factor simplex on the response surface, we choose a starting point (a, b) for the first vertex and place the remaining two vertices at (a + sa, b) and (a + 0.5sa, b + 0.87sb) where sa and sb are step sizes for factor A and for factor B [Long, D. E. Anal. Chim. Acta 1969, 46, 193–206]. The following set of rules moves the simplex across the response surface in search of the optimum response:
Rule 1. Rank the vertices from best (vb) to worst (vw).
Rule 2. Reject the worst vertex (vw) and replace it with a new vertex (vn) by reflecting the worst vertex through the midpoint of the remaining vertices. The new vertex’s factor levels are twice the average factor levels for the retained vertices minus the factor levels for the worst vertex. For a two-factor optimization, the equations are shown here where vs is the third vertex.
\[a_{v_n} = 2 \left( \frac {a_{v_b} + a_{v_s}} {2} \right) - a_{v_w} \label{14.3}\]
\[b_{v_n} = 2 \left( \frac {b_{v_b} + b_{v_s}} {2} \right) - b_{v_w} \label{14.4}\]
Rule 3. If the new vertex has the worst response, then return to the previous vertex and reject the vertex with the second worst response, (vs) calculating the new vertex’s factor levels using rule 2. This rule ensures that the simplex does not return to the previous simplex.
Rule 4. Boundary conditions are a useful way to limit the range of possible factor levels. For example, it may be necessary to limit a factor’s concentration for solubility reasons, or to limit the temperature because a reagent is thermally unstable. If the new vertex exceeds a boundary condition, then assign it the worst response and follow rule 3.
The variables a and b in equation \ref{14.3} and equation \ref{14.4} are the factor levels for factor A and for factor B, respectively. Problem 3 in the end-of-chapter problems asks you to derive these equations.
Because the size of the simplex remains constant during the search, this algorithm is called a fixed-sized simplex optimization. Example \(\PageIndex{1}\) illustrates the application of these rules.
Find the optimum for the response surface in Figure \(\PageIndex{9}\) using the fixed-sized simplex searching algorithm. Use (0, 0) for the initial factor levels and set each factor’s step size to 1.00.
Solution
Letting a = 0, b =0, sa = 1.00, and sb = 1.00 gives the vertices for the initial simplex as
\[\text{vertex 1:} (a, b) = (0, 0) \nonumber\]
\[\text{vertex 2:} (a + s_a, b) = (1.00, 0) \nonumber\]
\[\text{vertex 3:} (a + 0.5s_a, b + 0.87s_b) = (0.50, 0.87) \nonumber\]
The responses, from equation \ref{14.2}, for the three vertices are shown in the following table
| vertex | a | b | response |
|---|---|---|---|
| \(v_1\) | 0 | 0 | 5.50 |
| \(v_2\) | 1.00 | 0 | 6.85 |
| \(v_3\) | 0.50 | 0.87 | 6.68 |
with \(v_1\) giving the worst response and \(v_3\) the best response. Following Rule 1, we reject \(v_1\) and replace it with a new vertex using equation \ref{14.3} and equation \ref{14.4}; thus
\[a_{v_4} = 2 \left( \frac {1.00 + 0.50} {2} \right) - 0 = 1.50 \nonumber\]
\[b_{v_4} = 2 \left( \frac {0 + 0.87} {2} \right) - 0 = 0.87 \nonumber\]
The following table gives the vertices of the second simplex.
| vertex | a | b | response |
|---|---|---|---|
| \(v_2\) | 1.50 | 0 | 6.85 |
| \(v_3\) | 0.50 | 0.87 | 6.68 |
| \(v_4\) | 1.50 | 0.87 | 7.80 |
with \(v_3\) giving the worst response and \(v_4\) the best response. Following Rule 1, we reject \(v_3\) and replace it with a new vertex using equation \ref{14.3} and equation \ref{14.4}; thus
\[a_{v_5} = 2 \left( \frac {1.00 + 1.50} {2} \right) - 0.50 = 2.00 \nonumber\]
\[b_{v_5} = 2 \left( \frac {0 + 0.87} {2} \right) - 0.87 = 0 \nonumber\]
The following table gives the vertices of the third simplex.
| vertex | a | b | response |
|---|---|---|---|
| \(v_2\) | 1.50 | 0 | 6.85 |
| \(v_4\) | 1.50 | 0.87 | 780 |
| \(v_5\) | 2.00 | 0 | 7.90 |
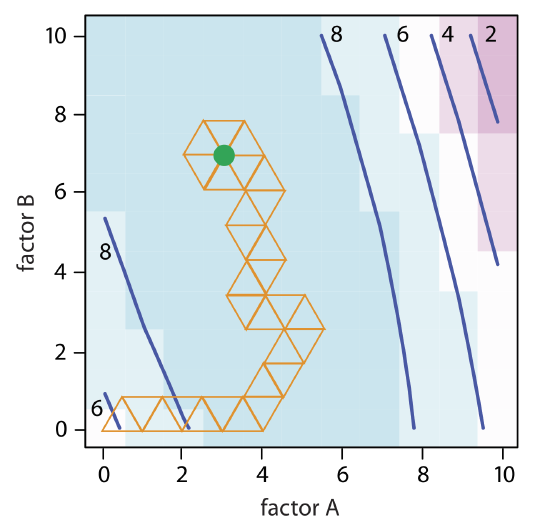
The calculation of the remaining vertices is left as an exercise. Figure \(\PageIndex{11}\) shows the progress of the complete optimization. After 29 steps the simplex begins to repeat itself, circling around the optimum response of (3, 7).
The size of the initial simplex ultimately limits the effectiveness and the efficiency of a fixed-size simplex searching algorithm. We can increase its efficiency by allowing the size of the simplex to expand or to contract in response to the rate at which we approach the optimum. For example, if we find that a new vertex is better than any of the vertices in the preceding simplex, then we expand the simplex further in this direction on the assumption that we are moving directly toward the optimum. Other conditions might cause us to contract the simplex—to make it smaller—to encourage the optimization to move in a different direction. We call this a variable-sized simplex optimization. Consult this chapter’s additional resources for further details of the variable-sized simplex optimization.
Mathematical Models of Response Surfaces
A response surface is described mathematically by an equation that relates the response to its factors. Equation \ref{14.1} and equation \ref{14.2} provide two examples of such mathematical models. If we measure the response for several combinations of factor levels, then we can model the response surface by using a regression analysis to fit an appropriate equation to the data. There are two broad categories of models that we can use for a regression analysis: theoretical models and empirical models.
Theoretical Models of the Response Surface
A theoretical model is derived from the known chemical and physical relationships between the response and its factors. In spectrophotometry, for example, Beer’s law is a theoretical model that relates an analyte’s absorbance, A, to its concentration, CA
\[A = \epsilon b C_A \nonumber\]
where \(\epsilon\) is the molar absorptivity and b is the pathlength of the electromagnetic radiation passing through the sample. A Beer’s law calibration curve, therefore, is a theoretical model of a response surface.
For a review of Beer’s law, see Chapter 10.2. Figure \(\PageIndex{1}\) in this chapter is an example of a Beer’s law calibration curve.
Empirical Models of the Response Surface
In many cases the underlying theoretical relationship between the response and its factors is unknown. We still can develop a model of the response surface if we make some reasonable assumptions about the underlying relationship between the factors and the response. For example, if we believe that the factors A and B are independent and that each has only a first-order effect on the response, then the following equation is a suitable model.
\[R = \beta_0 + \beta_a A + \beta_b B \nonumber\]
where R is the response, A and B are the factor levels, and \(\beta_0\), \(\beta_a\), and \(\beta_b\) are adjustable parameters whose values are determined by a linear regression analysis. Other examples of equations include those for dependent factors
\[R = \beta_0 + \beta_a A + \beta_b B + \beta_{ab} AB \nonumber\]
and those with higher-order terms.
\[R = \beta_0 + \beta_a A + \beta_b B + \beta_{aa} A^2 + \beta_{bb} B^2 \nonumber\]
Each of these equations provides an empirical model of the response surface because it has no basis in a theoretical understanding of the relationship between the response and its factors. Although an empirical model may provide an excellent description of the response surface over a limited range of factor levels, it has no basis in theory and we cannot reliably extend it to unexplored parts of the response surface.
The calculations for a linear regression when the model is first-order in one factor (a straight line) are described in Chapter 5.4. A complete mathematical treatment of linear regression for models that are second-order in one factor or which contain more than one factor is beyond the scope of this text. The computations for a few special cases, however, are straightforward and are considered in this section. A more comprehensive treatment of linear regression is available in several of this chapter’s additional resources.
Factorial Designs
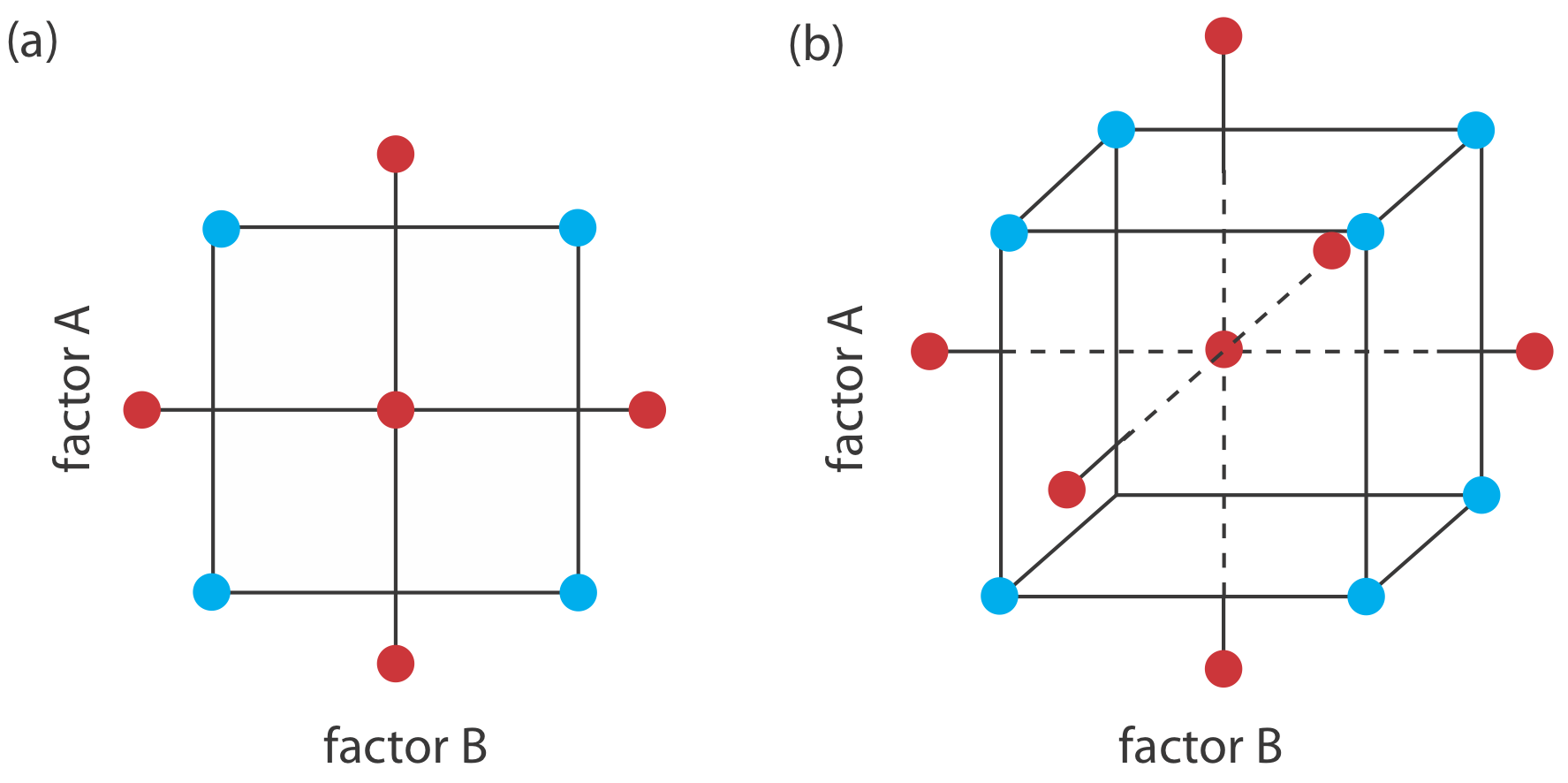
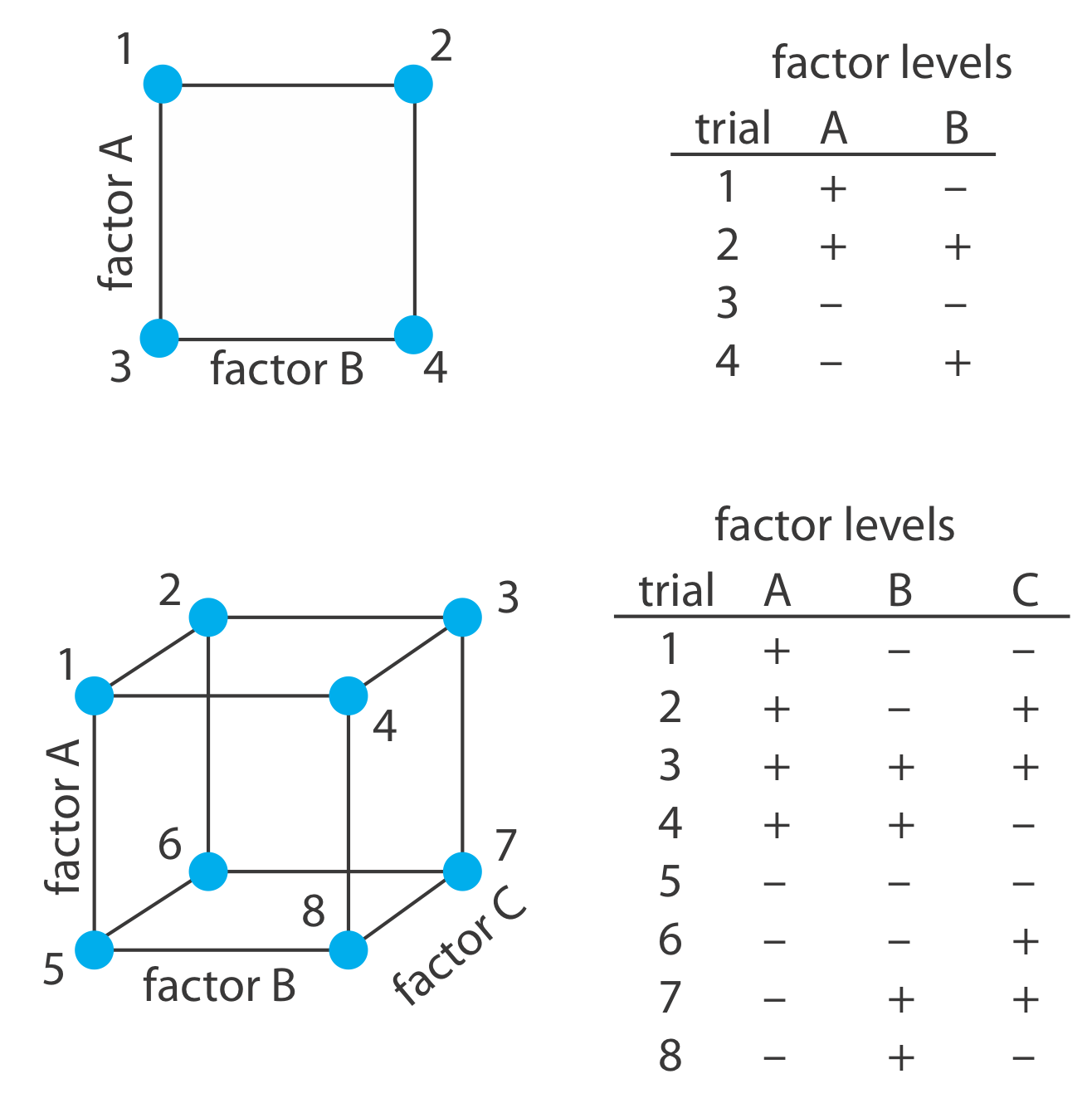
To build an empirical model we measure the response for at least two levels for each factor. For convenience we label these levels as high, Hf, and low, Lf, where f is the factor; thus HA is the high level for factor A and LB is the low level for factor B. If our empirical model contains more than one factor, then each factor’s high level is paired with both the high level and the low level for all other factors. In the same way, the low level for each factor is paired with the high level and the low level for all other factors. As shown in Figure \(\PageIndex{12}\), this requires 2k experiments where k is the number of factors. This experimental design is known as a 2k factorial design.
Another system of notation is to use a plus sign (+) to indicate a factor’s high level and a minus sign (–) to indicate its low level. We will use H or L when writing an equation and a plus sign or a minus sign in tables.
Coded Factor Levels
The calculations for a 2k factorial design are straightforward and easy to complete with a calculator or a spreadsheet. To simplify the calculations, we code the factor levels using \(+1\) for a high level and \(-1\) for a low level. Coding has two additional advantages: scaling the factors to the same magnitude makes it easier to evaluate each factor’s relative importance, and it places the model’s intercept, \(\beta_0\), at the center of the experimental design. As shown in Example \(\PageIndex{2}\), it is easy to convert between coded and uncoded factor levels.
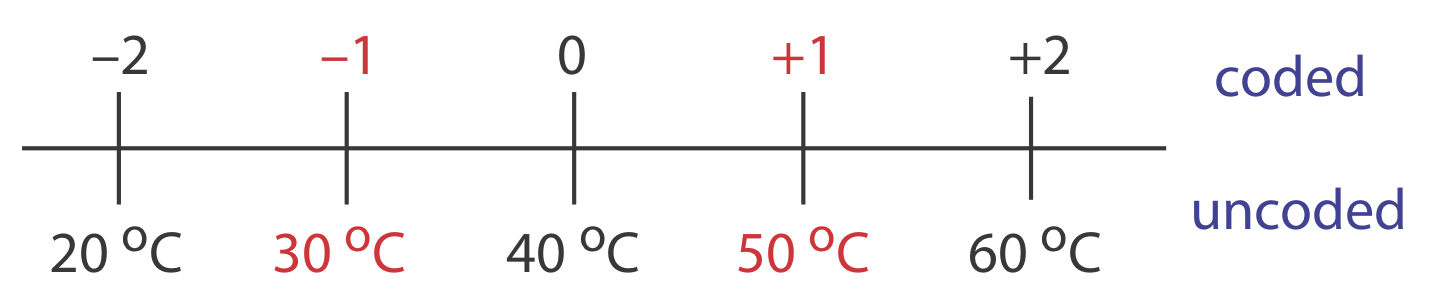
To explore the effect of temperature on a reaction, we assign 30oC to a coded factor level of \(-1\) and assign a coded level \(+1\) to a temperature of 50oC. What temperature corresponds to a coded level of \(-0.5\) and what is the coded level for a temperature of 60oC?
Solution
The difference between \(-1\) and \(+1\) is 2, and the difference between 30oC and 50oC is 20oC; thus, each unit in coded form is equivalent to 10oC in uncoded form. With this information, it is easy to create a simple scale between the coded and the uncoded values, as shown in Figure \(\PageIndex{13}\). A temperature of 35oC corresponds to a coded level of \(-0.5\) and a coded level of \(+2\) corresponds to a temperature of 60oC.
Determining the Empirical Model
Let’s begin by considering a simple example that involves two factors, A and B, and the following empirical model.
\[R = \beta_0 + \beta_a A + \beta_b B + \beta_{ab} AB \label{14.5}\]
A 2k factorial design with two factors requires four runs. Table \(\PageIndex{3}\) provides the uncoded levels (A and B), the coded levels (A* and B*), and the responses (R) for these experiments. The terms \(\beta_0\), \(\beta_a\), \(\beta_b\), and \(\beta_{ab}\) in equation \ref{14.5} account for, respectively, the mean effect (which is the average response), the first-order effects due to factor A and to factor B, and the interaction between the two factors.
Equation \ref{14.5} has four unknowns—the four beta terms—and Table \(\PageIndex{3}\) describes the four experiments. We have just enough information to calculate values for \(\beta_0\), \(\beta_a\), \(\beta_b\), and \(\beta_{ab}\). When working with the coded factor levels, the values of these parameters are easy to calculate using the following equations, where n is the number of runs.
\[\beta_{0} \approx b_{0}=\frac{1}{n} \sum_{i=1}^{n} R_{i} \label{14.6}\]
\[\beta_{a} \approx b_{a}=\frac{1}{n} \sum_{i=1}^{n} A^*_{i} R_{i} \label{14.7}\]
\[\beta_{b} \approx b_{b}=\frac{1}{n} \sum_{i=1}^{n} B^*_{i} R_{i} \label{14.8}\]
\[\beta_{ab} \approx b_{ab}=\frac{1}{n} \sum_{i=1}^{n} A^*_{i} B^*_{i} R_{i} \label{14.9}\]
Solving for the estimated parameters using the data in Table \(\PageIndex{3}\)
\[b_{0}=\frac{22.5+11.5+17.5+8.5}{4}=15.0 \nonumber\]
\[b_{a}=\frac{22.5+11.5-17.5-8.5}{4}=2.0 \nonumber\]
\[b_{b}=\frac{22.5-11.5+17.5-8.5}{4}=5.0 \nonumber\]
\[b_{ab}=\frac{22.5-11.5-17.5+8.5}{4}=0.5 \nonumber\]
leaves us with the coded empirical model for the response surface.
\[R = 15.0 + 2.0 A^* + 5.0 B^* + 0.05 A^* B^* \label{14.10}\]
Recall that we introduced coded factor levels with the promise that they simplify calculations. Although we can convert this coded model into its uncoded form, there is no need to do so. If we need to know the response for a new set of factor levels, we just convert them into coded form and calculate the response. For example, if A is 10 and B is 15, then A* is 0 and B* is –0.5. Substituting these values into equation \ref{14.10} gives a response of 12.5.
We can extend this approach to any number of factors. For a system with three factors—A, B, and C—we can use a 23 factorial design to determine the parameters in the following empirical model
\[R = \beta_0 + \beta_a A + \beta_b B + \beta_c C + \beta_{ab} AB + \beta_{ac} AC + \beta_{bc} BC + \beta_{abc} ABC \label{14.11}\]
where A, B, and C are the factor levels. The terms \(\beta_0\), \(\beta_a\), \(\beta_b\), and \(\beta_{ab}\) are estimated using equation \ref{14.6}, equation \ref{14.7}, equation \ref{14.8}, and equation \ref{14.9}, respectively. To find estimates for the remaining parameters we use the following equations.
\[\beta_{c} \approx b_{c}=\frac{1}{n} \sum_{i=1}^{n} C^*_{i} R \label{14.12}\]
\[\beta_{ac} \approx b_{ac}=\frac{1}{n} \sum_{i=1}^{n} A^*_{i} C^*_{i} R \label{14.13}\]
\[\beta_{bc} \approx b_{bc}=\frac{1}{n} \sum_{i=1}^{n} B^*_{i} C^*_{i} R \label{14.14}\]
\[\beta_{abc} \approx b_{abc}=\frac{1}{n} \sum_{i=1}^{n} A^*_{i} B^*_{i} C^*_{i} R \label{14.15}\]
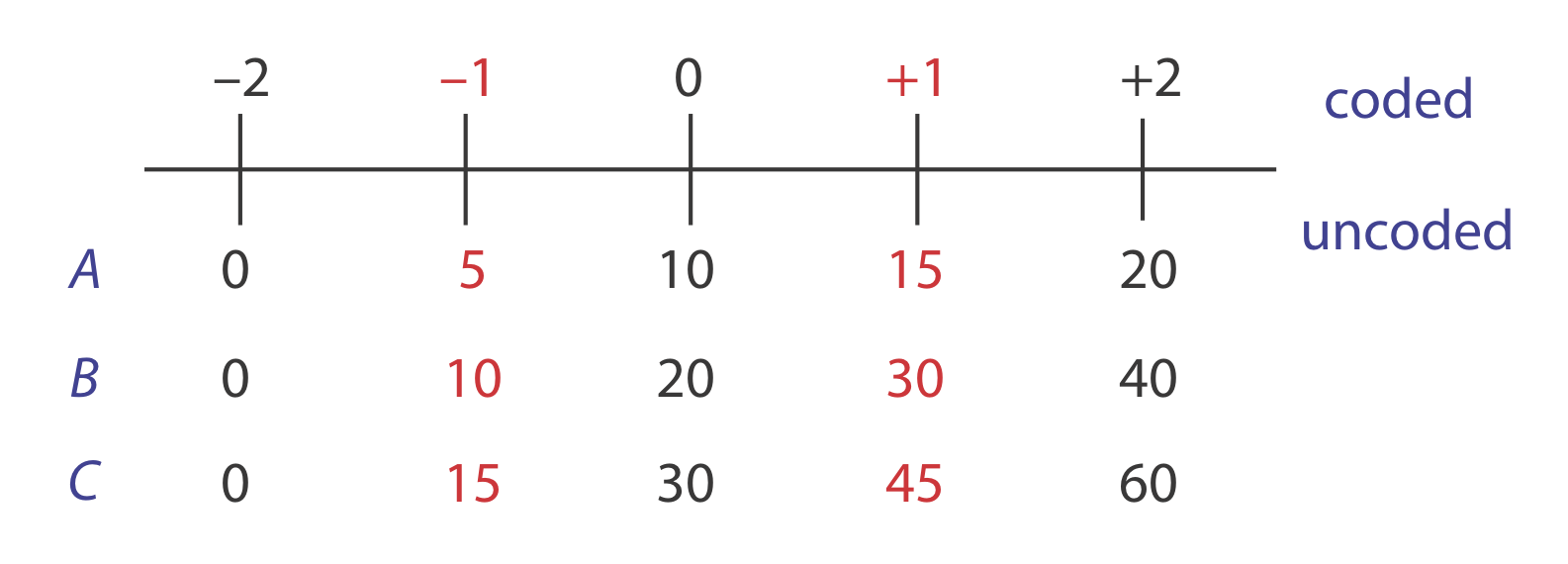
Table \(\PageIndex{4}\) lists the uncoded factor levels, the coded factor levels, and the responses for a 23 factorial design. Determine the coded empirical model for the response surface based on equation \ref{14.11}. What is the expected response when A is 10, B is 15, and C is 50?
Solution
Equation \ref{14.11} has eight unknowns—the eight beta terms—and Table \(\PageIndex{4}\) describes eight experiments. We have just enough information to calculate values for \(\beta_0\), \(\beta_a\), \(\beta_b\), \(\beta_{ab}\), \(\beta_{ac}\), \(\beta_{bc}\), and \(\beta_{abc}\); these values are
\[b_{0}=\frac{1}{8} \times(137.25+54.75+73.75+30.25+61.75+30.25+41.25+18.75 )=56.0 \nonumber\]
\[b_{a}=\frac{1}{8} \times(137.25+54.75+73.75+30.25-61.75-30.25-41.25-18.75 )=18.0 \nonumber\]
\[b_{b}=\frac{1}{8} \times(137.25+54.75-73.75-30.25+61.75+30.25-41.25-18.75 )=15.0 \nonumber\]
\[b_{c}=\frac{1}{8} \times(137.25-54.75+73.75-30.25+61.75-30.25+41.25-18.75 )=22.5 \nonumber\]
\[b_{ab}=\frac{1}{8} \times(137.25+54.75-73.75-30.25-61.75-30.25+41.25+18.75 )=7.0 \nonumber\]
\[b_{ac}=\frac{1}{8} \times(137.25-54.75+73.75-30.25-61.75+30.25-41.25+18.75 )=9.0 \nonumber\]
\[b_{bc}=\frac{1}{8} \times(137.25-54.75-73.75+30.25+61.75-30.25-41.25+18.75 )=6.0 \nonumber\]
\[b_{abc}=\frac{1}{8} \times(137.25-54.75-73.75+30.25-61.75+30.25+41.25-18.75 )=3.75 \nonumber\]
The coded empirical model, therefore, is
\[R = 56.0 + 18.0 A^* + 15.0 B^* + 22.5 C^* + 7.0 A^* B^* + 9.0 A^* C^* + 6.0 B^* C^* + 3.75 A^* B^* C^* \nonumber\]
To find the response when A is 10, B is 15, and C is 50, we first convert these values into their coded form. Figure \(\PageIndex{14}\) helps us make the appropriate conversions; thus, A* is 0, B* is \(-0.5\), and C* is \(+1.33\). Substituting back into the empirical model gives a response of
\[R = 56.0 + 18.0 (0) + 15.0 (-0.5) + 22.5 (+1.33) + 7.0 (0) (-0.5) + 9.0 (0) (+1.33) + 6.0 (-0.5) (+1.33) + 3.75 (0) (-0.5) (+1.33) = 74.435 \approx 74.4 \nonumber\]
A 2k factorial design can model only a factor’s first-order effect, including first-order interactions, on the response. A 22 factorial design, for example, includes each factor’s first-order effect (\(\beta_a\) and \(\beta_b\)) and a first-order interaction between the factors (\(\beta_{ab}\)). A 2k factorial design cannot model higher-order effects because there is insufficient information. Here is simple example that illustrates the problem. Suppose we need to model a system in which the response is a function of a single factor, A. Figure \(\PageIndex{15}\)a shows the result of an experiment using a 21 factorial design. The only empirical model we can fit to the data is a straight line.
\[R = \beta_0 + \beta_a A \nonumber\]
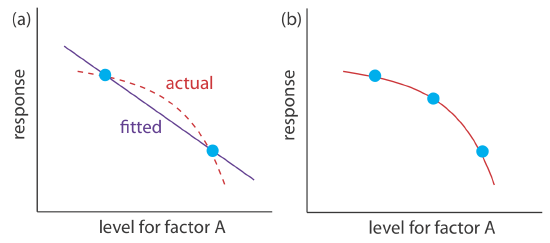
If the actual response is a curve instead of a straight-line, then the empirical model is in error. To see evidence of curvature we must measure the response for at least three levels for each factor. We can fit the 31 factorial design in Figure \(\PageIndex{15}\)b to an empirical model that includes second-order factor effects.
\[R = \beta_0 + \beta_a A + \beta_{aa} A^2 \nonumber\]
In general, an n-level factorial design can model single-factor and interaction terms up to the (n – 1)th order.
We can judge the effectiveness of a first-order empirical model by measuring the response at the center of the factorial design. If there are no higher-order effects, then the average response of the trials in a 2k factorial design should equal the measured response at the center of the factorial design. To account for influence of random errors we make several determinations of the response at the center of the factorial design and establish a suitable confidence interval. If the difference between the two responses is significant, then a first-order empirical model probably is inappropriate.
One of the advantages of working with a coded empirical model is that b0 is the average response of the 2 \(\times\) k trials in a 2k factorial design.
One method for the quantitative analysis of vanadium is to acidify the solution by adding H2SO4 and oxidizing the vanadium with H2O2 to form a red-brown soluble compound with the general formula (VO)2(SO4)3. Palasota and Deming studied the effect of the relative amounts of H2SO4 and H2O2 on the solution’s absorbance, reporting the following results for a 22 factorial design [Palasota, J. A.; Deming, S. N. J. Chem. Educ. 1992, 62, 560–563].
| H2SO4 | H2O2 | absorbance |
|---|---|---|
| \(+1\) | \(+1\) | 0.330 |
| \(+1\) | \(-1\) | 0.359 |
| \(-1\) | \(+1\) | 0.293 |
| \(-1\) | \(-1\) | 0.420 |
Four replicate measurements at the center of the factorial design give absorbances of 0.334, 0.336, 0.346, and 0.323. Determine if a first-order empirical model is appropriate for this system. Use a 90% confidence interval when accounting for the effect of random error.
Solution
We begin by determining the confidence interval for the response at the center of the factorial design. The mean response is 0.335 with a standard deviation of 0.0094, which gives a 90% confidence interval of
\[\mu=\overline{X} \pm \frac{t s}{\sqrt{n}}=0.335 \pm \frac{(2.35)(0.0094)}{\sqrt{4}}=0.335 \pm 0.011 \nonumber\]
The average response, \(\overline{R}\), from the factorial design is
\[\overline{R}=\frac{0.330+0.359+0.293+0.420}{4}=0.350 \nonumber\]
Because \(\overline{R}\) exceeds the confidence interval’s upper limit of 0.346, we can reasonably assume that a 22 factorial design and a first-order empirical model are inappropriate for this system at the 95% confidence level.
Central Composite Designs
One limitation to a 3k factorial design is the number of trials we need to run. As shown in Figure \(\PageIndex{16}\) , a 32 factorial design requires 9 trials. This number increases to 27 for three factors and to 81 for 4 factors.
A more efficient experimental design for a system that contains more than two factors is a central composite design, two examples of which are shown in Figure \(\PageIndex{17}\). The central composite design consists of a 2k factorial design, which provides data to estimate each factor’s first-order effect and interactions between the factors, and a star design that has \(2^k + 1\) points, which provides data to estimate second-order effects. Although a central composite design for two factors requires the same number of trials, nine, as a 32 factorial design, it requires only 15 trials and 25 trials when using three factors or four factors. See this chapter’s additional resources for details about the central composite designs.