6.6: Ladder Diagrams
- Page ID
- 220703
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)When we develop or evaluate an analytical method, we often need to understand how the chemistry that takes place affects our results. Suppose we wish to isolate Ag+ by precipitating it as AgCl. If we also need to control pH, then we must use a reagent that does not adversely affect the solubility of AgCl. It is a mistake to use NH3 to adjust the pH, for example, because it increases the solubility of AgCl (see reaction 6.5.4). One of the primary sources of determinate errors in many analytical methods is failing to account for potential chemical interferences.
In this section we introduce the ladder diagram as a simple graphical tool for visualizing equilibrium chemistry. We will use ladder diagrams to determine what reactions occur when we combine several reagents, to estimate the approximate composition of a system at equilibrium, and to evaluate how a change to solution conditions might affect an analytical method.
Although not specifically on the topic of ladder diagrams as developed in this section, the following papers provide appropriate background information: (a) Runo, J. R.; Peters, D. G. J. Chem. Educ. 1993, 70, 708–713; (b) Vale, J.; Fernández‐Pereira, C.; Alcalde, M. J. Chem. Educ. 1993, 70, 790–795; (c) Fernández‐Pereira, C.; Vale, J. Chem. Educator 1996, 6, 1–18; (d) Fernández‐ Pereira, C.; Vale, J.; Alcalde, M. Chem. Educator 2003, 8, 15–21; (e) Fernández‐Pereira, C.; Alcalde, M.; Villegas, R.; Vale, J. J. Chem. Educ. 2007, 84, 520–525. Ladder diagrams are a great tool for helping you to think intuitively about analytical chemistry. We will make frequent use of them in the chapters to follow.
Ladder Diagrams for Acid–Base Equilibria
Let’s use acetic acid, CH3COOH, to illustrate the process we will use to draw and to interpret an acid–base ladder diagram. Before we draw the diagram, however, let’s consider the equilibrium reaction in more detail. Acetic acid's acid dissociation reaction and equilibrium constant expression are
\[\mathrm{CH}_{3} \mathrm{COOH}(a q)+\mathrm{H}_{2} \mathrm{O}(l)\rightleftharpoons \mathrm{H}_{3} \mathrm{O}^{+}(a q)+\mathrm{CH}_{3} \mathrm{COO}^{-}(a q) \nonumber\]
\[K_{\mathrm{a}}=\frac{\left[\mathrm{CH}_{3} \mathrm{COO}^{-}\right]\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]}{\left[\mathrm{CH}_{3} \mathrm{COOH}\right]}=1.75 \times 10^{-5} \nonumber\]
First, let’s take the logarithm of each term in this equation and multiply through by –1
\[-\log K_{a}=4.76=-\log \left[\mathrm{H}_{3} \mathrm{O}^{+}\right]-\log \frac{\left[\mathrm{CH}_{3} \mathrm{COO}^{-}\right]}{\left[\mathrm{CH}_{3} \mathrm{COOH}\right]} \nonumber\]
Now, let’s replace –log[H3O+] with pH and rearrange the equation to obtain the result shown here.
\[\mathrm{pH}=4.76+\log \frac{\left[\mathrm{CH}_{3} \mathrm{COO}^{-}\right]}{\left[\mathrm{CH}_{3} \mathrm{COOH}\right]} \label{6.1}\]
Equation \ref{6.1} tells us a great deal about the relationship between pH and the relative amounts of acetic acid and acetate at equilibrium. If the concentrations of CH3COOH and CH3COO– are equal, then equation \ref{6.1} reduces to
\[\mathrm{pH}=4.76+\log (1)=4.76+0=4.76 \nonumber\]
If the concentration of CH3COO– is greater than that of CH3COOH, then the log term in equation \ref{6.1} is positive and the pH is greater than 4.76. This is a reasonable result because we expect the concentration of the conjugate base, CH3COO–, to increase as the pH increases. Similar reasoning will convince you that the pH is less than 4.76 when the concentration of CH3COOH exceeds that of CH3COO–.
Now we are ready to construct acetic acid’s ladder diagram (Figure \(\PageIndex{1}\)). First, we draw a vertical arrow that represents the solution’s pH, with smaller (more acidic) pH levels at the bottom and larger (more basic) pH levels at the top. Second, we draw a horizontal line at a pH equal to acetic acid’s pKa value. This line, or step on the ladder, divides the pH axis into regions where either CH3COOH or CH3COO– is the predominate species. This completes the ladder diagram.
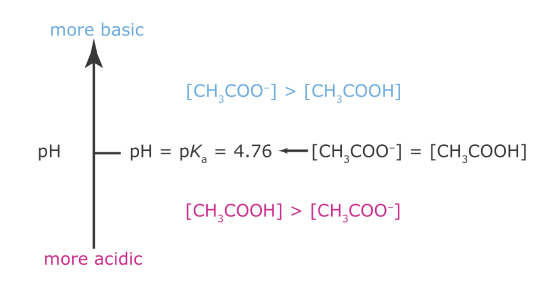
Using the ladder diagram, it is easy to identify the predominate form of acetic acid at any pH. At a pH of 3.5, for example, acetic acid exists primarily as CH3COOH. If we add sufficient base to the solution such that the pH increases to 6.5, the predominate form of acetic acid is CH3COO–.
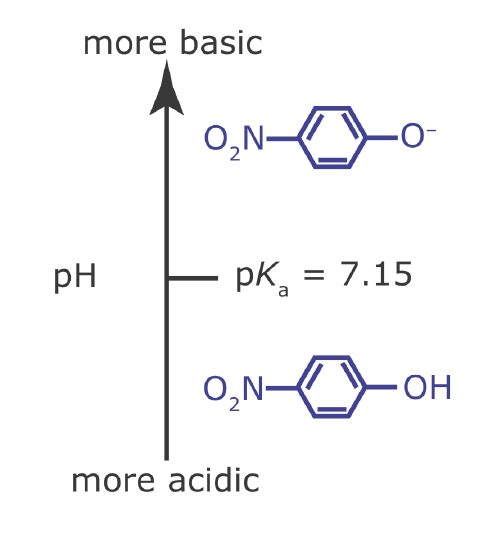
Draw a ladder diagram for the weak base p‐nitrophenolate and identify its predominate form at a pH of 6.00.
Solution
To draw a ladder diagram for a weak base, we simply draw the ladder diagram for its conjugate weak acid. From Appendix 11, the pKa for p‐nitrophenol is 7.15. The resulting ladder diagram is shown in Figure \(\PageIndex{2}\). At a pH of 6.00, p‐nitrophenolate is present primarily in its weak acid form.
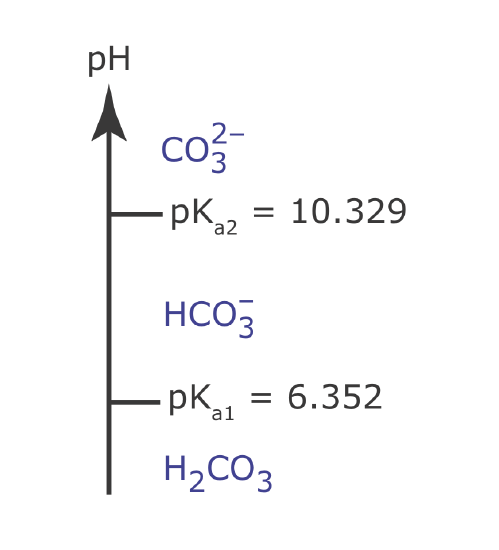
Draw a ladder diagram for carbonic acid, H2CO3. Because H2CO3 is a diprotic weak acid, your ladder diagram will have two steps. What is the predominate form of carbonic acid when the pH is 7.00? Relevant equilibrium constants are in Appendix 11.
- Answer
-
From Appendix 11, the pKa values for H2CO3 are 6.352 and 10.329. The ladder diagram for H2CO3 is shown below. The predominate form at a pH of 7.00 is \(\text{HCO}_3^-\).
A ladder diagram is particularly useful for evaluating the reactivity between a weak acid and a weak base. Figure \(\PageIndex{3}\), for example, shows a single ladder diagram for acetic acid/acetate and for p‐nitrophenol/p‐nitrophenolate. An acid and a base can not co‐exist if their respective areas of predominance do not overlap. If we mix together solutions of acetic acid and sodium p‐nitrophenolate, the reaction
\[\mathrm{C}_{6} \mathrm{H}_{4} \mathrm{NO}_{2}^{-}(a q)+\mathrm{CH}_{3} \mathrm{COOH}(a q)\rightleftharpoons \text{CH}_3\text{COO}^-(aq) + \text{C}_6\text{H}_4\text{NO}_2\text{H}(aq) \label{6.2}\]
occurs because the areas of predominance for acetic acid and p‐nitrophenolate do not overlap. The solution’s final composition depends on which species is the limiting reagent. The following example shows how we can use the ladder diagram in Figure \(\PageIndex{3}\) to evaluate the result of mixing together solutions of acetic acid and p‐nitrophenolate.
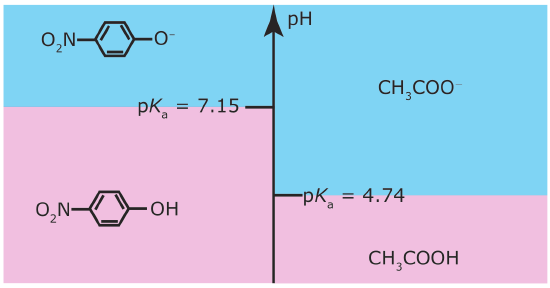
Predict the approximate pH and the final composition after mixing together 0.090 moles of acetic acid and 0.040 moles of p‐nitrophenolate.
Solution
The ladder diagram in Figure \(\PageIndex{3}\) indicates that the reaction between acetic acid and p‐nitrophenolate is favorable. Because acetic acid is in excess, we assume the reaction of p‐nitrophenolate to p‐nitrophenol is complete. At equilibrium essentially no p‐nitrophenolate remains and there are 0.040 mol of p‐nitrophenol. Converting p‐nitrophenolate to p‐nitrophenol consumes 0.040 moles of acetic acid; thus
\[\begin{array}{c}{\text { moles } \mathrm{CH}_{3} \mathrm{COOH}=0.090-0.040=0.050 \ \mathrm{mol}} \\ {\text { moles } \mathrm{CH}_{3} \mathrm{COO}^{-}=0.040 \ \mathrm{mol}}\end{array} \nonumber\]
According to the ladder diagram, the pH is 4.74 when there are equal amounts of CH3COOH and CH3COO–. Because we have slightly more CH3COOH than CH3COO–, the pH is slightly less than 4.74.
Using Figure \(\PageIndex{3}\), predict the approximate pH and the composition of the solution formed by mixing together 0.090 moles of p‐nitrophenolate and 0.040 moles of acetic acid.
- Answer
-
The ladder diagram in Figure \(\PageIndex{3}\) indicates that the reaction between acetic acid and p‐nitrophenolate is favorable. Because p‐nitrophenolate is in excess, we assume the reaction of acetic acid to acetate is complete. At equilibrium essentially no acetic acid remains and there are 0.040 moles of acetate. Converting acetic acid to acetate consumes 0.040 moles of p‐nitrophenolate; thus
\[\text { moles } p \text {-nitrophenolate }=0.090-0.040=0.050 \text { mol } \nonumber\]
\[\text { moles } p\text{-nitrophenol }=0.040 \ \mathrm{mol} \nonumber\]
According to the ladder diagram for this system, the pH is 7.15 when there are equal concentrations of p‐nitrophenol and p‐nitrophenolate. Because we have slightly more p‐nitrophenolate than we have p‐nitrophenol, the pH is slightly greater than 7.15.
If the areas of predominance for an acid and a base overlap, then we do not expect that much of a reaction will occur. For example, if we mix together solutions of CH3COO– and p‐nitrophenol, we do not expect a significant change in the moles of either reagent. Furthermore, the pH of the mixture must be between 4.76 and 7.15, with the exact pH depending upon the relative amounts of CH3COO– and p‐nitrophenol.
We also can use an acid–base ladder diagram to evaluate the effect of pH on other equilibria. For example, the solubility of CaF2
\[\mathrm{CaF}_{2}(s) \rightleftharpoons \mathrm{Ca}^{2+}(a q)+2 \mathrm{F}^{-}(a q) \nonumber\]
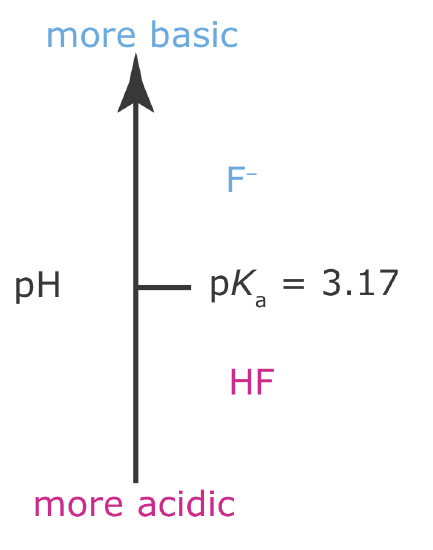
is affected by pH because F– is a weak base. From Le Châtelier’s principle, we know that converting F– to HF will increase the solubility of CaF2. To minimize the solubility of CaF2 we need to maintain the solution’s pH so that F– is the predominate species. The ladder diagram for HF (Figure \(\PageIndex{4}\)) shows us that maintaining a pH of more than 3.17 will minimize solubility losses.
Ladder Diagrams for Complexation Equilibria
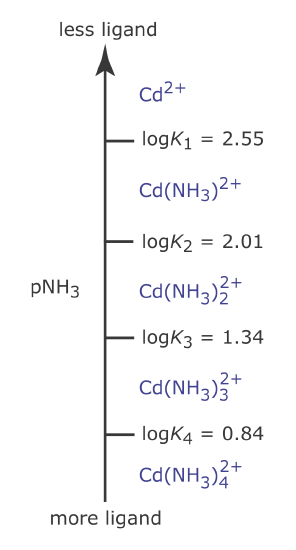
We can apply the same principles for constructing and interpreting an acid–base ladder diagram to equilibria that involve metal–ligand complexes. For a complexation reaction we define the ladder diagram’s scale using the concentration of uncomplexed, or free ligand, pL. Using the formation of \(\text{Cd(NH}_3)^{2+}\) as an example
\[\mathrm{Cd}^{2+}(a q)+\mathrm{NH}_{3}(a q) \rightleftharpoons \mathrm{Cd}\left(\mathrm{NH}_{3}\right)^{2+}(a q) \nonumber\]
we can show that log K1 is the dividing line between the areas of predominance for Cd2+ and for \(\text{Cd(NH}_3)^{2+}\).
\[K_{1}=3.55 \times 10^{2}=\frac{\left[\mathrm{Cd}\left(\mathrm{NH}_{3}\right)^{2+}\right]}{\left[\mathrm{Cd}^{2+}\right]\left[\mathrm{NH}_{3}\right]} \nonumber\]
\[\log K_{1}=\log \left(3.55 \times 10^{2}\right)=\log \frac{\left[\mathrm{Cd}\left(\mathrm{NH}_{3}\right)^{2+}\right]}{\left[\mathrm{Cd}^{2+}\right]}-\log \left[\mathrm{NH}_{3}\right] \nonumber\]
\[\log K_{1}=2.55=\log \frac{\left[\mathrm{Cd}\left(\mathrm{NH}_{3}\right)^{2+}\right]}{\left[\mathrm{Cd}^{2+}\right]}+\mathrm{p} \mathrm{NH}_{3} \nonumber\]
\[\mathrm{p} \mathrm{NH}_{3}=\log K_{1}+\log \frac{\left[\mathrm{Cd}^{2+}\right]}{\left[\mathrm{Cd}\left(\mathrm{NH}_{3}\right)^{2+}\right]}=2.55+\log \frac{\left[\mathrm{Cd}^{2+}\right]}{\left[\mathrm{Cd}\left(\mathrm{NH}_{3}\right)^{2+}\right]} \nonumber\]
Thus, Cd2+ is the predominate species when pNH3 is greater than 2.55 (a concentration of NH3 smaller than \(2.82 \times 10^{-3}\) M) and for a pNH3 value less than 2.55, \(\text{Cd(NH}_3)^{2+}\) is the predominate species. Figure \(\PageIndex{5}\) shows a complete metal–ligand ladder diagram for Cd2+ and NH3 that includes additional Cd–NH3 complexes.
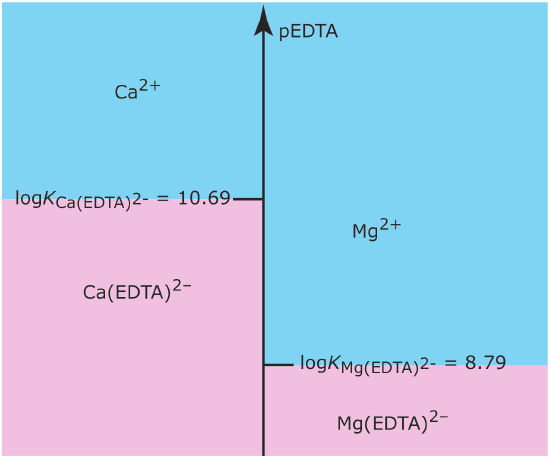
Draw a single ladder diagram for the Ca(EDTA)2– and the Mg(EDTA)2– metal–ligand complexes. Use your ladder diagram to predict the result of adding 0.080 moles of Ca2+ to 0.060 moles of Mg(EDTA)2–. EDTA is an abbreviation for the ligand ethylenediaminetetraacetic acid.
Solution
Figure \(\PageIndex{6}\) shows the ladder diagram for this system of metal–ligand complexes. Because the predominance regions for Ca2+ and Mg(EDTA)2‐ do not overlap, the reaction
\[\mathrm{Ca}^{2+}(a q)+\mathrm{Mg}(\mathrm{EDTA})^{2-}(a q) \rightleftharpoons \mathrm{Ca}(\mathrm{EDTA})^{2-}(a q)+\mathrm{Mg}^{2+}(a q) \nonumber\]
proceeds essentially to completion. Because Ca2+ is the excess reagent, the composition of the final solution is approximately
\[\text { moles } \mathrm{Ca}^{2+}=0.080-0.060=0.020 \ \mathrm{mol} \nonumber\]
\[\text { moles } \mathrm{Ca}(\mathrm{EDTA})^{2-}=0.060 \ \mathrm{mol} \nonumber\]
\[\text { moles } \mathrm{Mg}^{2+}=0.060 \ \mathrm{mol} \nonumber\]
\[\text { moles } \mathrm{Mg}(\mathrm{EDTA})^{2-}=0 \ \mathrm{mol} \nonumber\]
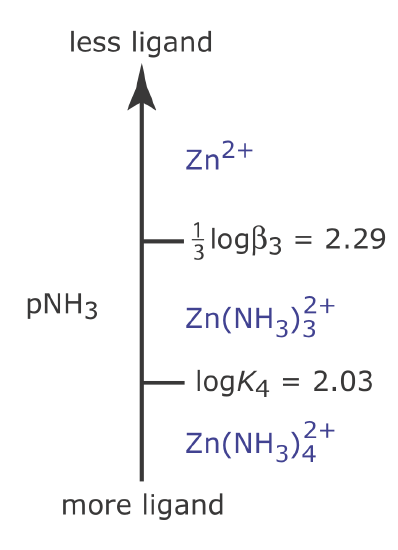
The metal–ligand ladder diagram in Figure \(\PageIndex{5}\) uses stepwise formation constants. We also can construct a ladder diagram using cumulative formation constants. For example, the first three stepwise formation constants for the reaction of Zn2+ with NH3
\[\mathrm{Zn}^{2+}(a q)+\mathrm{NH}_{3}(a q) \rightleftharpoons \mathrm{Zn}\left(\mathrm{NH}_{3}\right)^{2+}(a q) \quad K_{1}=1.6 \times 10^{2} \nonumber\]
\[\mathrm{Zn}\left(\mathrm{NH}_{3}\right)^{2+}(a q)+\mathrm{NH}_{3}(a q)\rightleftharpoons\mathrm{Zn}\left(\mathrm{NH}_{3}\right)_{2}^{2+}(a q) \quad K_{2}=1.95 \times 10^{2} \nonumber\]
\[\mathrm{Zn}\left(\mathrm{NH}_{3}\right)_{2}^{2+}(a q)+\mathrm{NH}_{3}(a q)=\mathrm{Zn}\left(\mathrm{NH}_{3}\right)_{3}^{2+}(a q) \quad K_{3}=2.3 \times 10^{2} \nonumber\]
suggests that the formation of \(\text{Zn(NH}_3)_3^{2+}\) is more favorable than the formation of \(\text{Zn(NH}_3)^{2+}\) or \(\text{Zn(NH}_3)_2^{2+}\). For this reason, the equilibrium is best represented by the cumulative formation reaction shown here.
\[\mathrm{Zn}^{2+}(a q)+3 \mathrm{NH}_{3}(a q)\rightleftharpoons \mathrm{Zn}\left(\mathrm{NH}_{3}\right)_{3}^{2+}(a q) \quad \beta_{3}=7.2 \times 10^{6} \nonumber\]
Because K3 is greater than K2, which is greater than K1, the formation of the metal‐ligand complex \(\text{Zn(NH}_3)_3^{2+}\) is more favorable than the formation of the other metal ligand complexes. For this reason, at lower values of pNH3 the concentration of \(\text{Zn(NH}_3)_3^{2+}\) is larger than the concentrations of \(\text{Zn(NH}_3)^{2+}\) or \(\text{Zn(NH}_3)_2^{2+}\). The value of \(\beta_3\) is
\[\beta_{3}=K_{1} \times K_{2} \times K_{3} \nonumber\]
To see how we incorporate this cumulative formation constant into a ladder diagram, we begin with the reaction’s equilibrium constant expression.
\[\beta_{3}=\frac{\left[\mathrm{Zn}\left(\mathrm{NH}_{3}\right)_{3}^{2+}\right]}{\left[\mathrm{Zn}^{2+}\right]\left[\mathrm{NH}_{3}\right]^{3}} \nonumber\]
Taking the log of each side
\[\log \beta_{3}=\log \frac{\left[\mathrm{Zn}\left(\mathrm{NH}_{3}\right)_{3}^{2+}\right]}{\left[\mathrm{Zn}^{2+}\right]}-3 \log \left[\mathrm{NH}_{3}\right] \nonumber\]
and rearranging gives
\[\mathrm{pNH}_{3}=\frac{1}{3} \log \beta_{3}+\frac{1}{3} \log \frac{\left[\mathrm{Zn}^{2+}\right]}{\left[\mathrm{Zn}\left(\mathrm{NH}_{3}\right)_{3}^{2+}\right]} \nonumber\]
When the concentrations of Zn and \(\text{Zn(NH}_3)_3^{2+}\) are equal, then
\[\mathrm{p} \mathrm{NH}_{3}=\frac{1}{3} \log \beta_{3}=2.29 \nonumber\]
In general, for the metal–ligand complex MLn, the step for a cumulative formation constant is
\[\mathrm{pL}=\frac{1}{n} \log \beta_{n} \nonumber\]
Figure \(\PageIndex{7}\) shows the complete ladder diagram for the Zn2+–NH3 system.
Ladder Diagrams for Oxidation/Reduction Equilibria
We also can construct ladder diagrams to help us evaluate redox equilibria. Figure \(\PageIndex{8}\) shows a typical ladder diagram for two half‐reactions in which the scale is the potential, E.
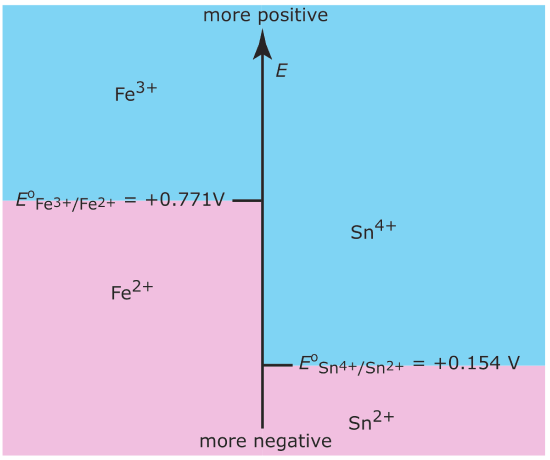
The Nernst equation defines the areas of predominance. Using the Fe3+/Fe2+ half‐reaction as an example, we write
\[E=E^{\circ}-\frac{R T}{n F} \ln \frac{\left[\mathrm{Fe}^{2+}\right]}{\left[\mathrm{Fe}^{3+}\right]}=0.771-0.05916 \log \frac{\left[\mathrm{Fe}^{2+}\right]}{\left[\mathrm{Fe}^{3+}\right]} \nonumber\]
At a potential more positive than the standard state potential, the predominate species is Fe3+, whereas Fe2+ predominates at potentials more negative than Eo. When coupled with the step for the Sn4+/Sn2+ half‐reaction we see that Sn2+ is a useful reducing agent for Fe3+. If Sn2+ is in excess, the potential of the resulting solution is near +0.154 V.
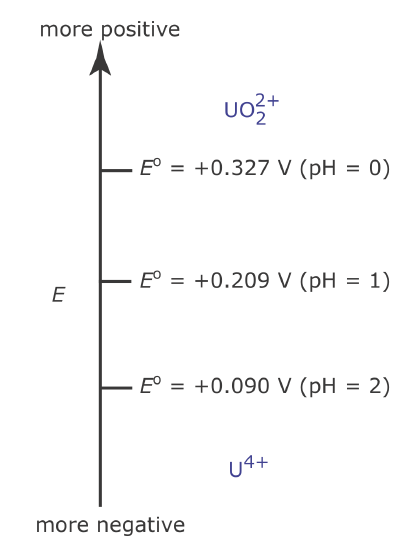
Because the steps on a redox ladder diagram are standard state potentials, a complication arises if solutes other than the oxidizing agent and reducing agent are present at non‐standard state concentrations. For example, the potential for the half‐reaction
\[\mathrm{UO}_{2}^{2+}(a q)+4 \mathrm{H}_{3} \mathrm{O}^{+}(a q)+2 e^{-} \rightleftharpoons \mathrm{U}^{4+}(a q)+6 \mathrm{H}_{2} \mathrm{O}(l) \nonumber\]
depends on the solution’s pH. To define areas of predominance in this case we begin with the Nernst equation
\[E=+0.327-\frac{0.05916}{2} \log \frac{\left[\mathrm{U}^{4+}\right]}{\left[\mathrm{UO}_{2}^{2+}\right]\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]^{4}} \nonumber\]
and factor out the concentration of H3O+.
\[E=+0.327+\frac{0.05916}{2} \log \left[\mathrm{H}_{3} \mathrm{O}^{+}\right]^{4}-\frac{0.05916}{2} \log \frac{\left[\mathrm{U}^{4+}\right]}{\left[\mathrm{UO}_{2}^{2+}\right]}\nonumber\]
From this equation we see that the area of predominance for \(\text{UO}_2^{2+}\) and U4+ is defined by a step at a potential where [U4+] = [\(\text{UO}_2^{2+}\)].
\[E=+0.327+\frac{0.05916}{2} \log \left[\mathrm{H}_{3} \mathrm{O}^{+}\right]^{4}=+0.327-0.1183 \mathrm{pH} \nonumber\]
Figure \(\PageIndex{9}\) shows how pH affects the step for the \(\text{UO}_2^{2+}\) /U4+ half‐reaction.