4.2: Characterizing Experimental Errors
- Page ID
- 220677
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Characterizing a penny’s mass using the data in Table 4.1.1 suggests two quesions. First, does our measure of central tendency agree with the penny’s expected mass? Second, why is there so much variability in the individual results? The first of these questions addresses the accuracy of our measurements and the second addresses the precision of our measurements. In this section we consider the types of experimental errors that affect accuracy and precision.
Errors That Affect Accuracy
Accuracy is how close a measure of central tendency is to its expected value, \(\mu\). We express accuracy either as an absolute error, e
\[e = \overline{X} - \mu \label{4.1}\]
or as a percent relative error, %e
\[\% e = \frac {\overline{X} - \mu} {\mu} \times 100 \label{4.2}\]
Although Equation \ref{4.1} and Equation \ref{4.2} use the mean as the measure of central tendency, we also can use the median.
The convention for representing a statistical parameter is to use a Roman letter for a value calculated from experimental data, and a Greek letter for its corresponding expected value. For example, the experimentally determined mean is \(\overline{X}\) and its underlying expected value is \(\mu\). Likewise, the experimental standard deviation is s and the underlying expected value is \(\sigma\).
We identify as determinate an error that affects the accuracy of an analysis. Each source of a determinate error has a specific magnitude and sign. Some sources of determinate error are positive and others are negative, and some are larger in magnitude and others are smaller in magnitude. The cumulative effect of these determinate errors is a net positive or negative error in accuracy.
It is possible, although unlikely, that the positive and negative determinate errors will offset each other, producing a result with no net error in accuracy.
We assign determinate errors into four categories—sampling errors, method errors, measurement errors, and personal errors—each of which we consider in this section.
Sampling Errors
A determinate sampling error occurs when our sampling strategy does not provide a us with a representative sample. For example, if we monitor the environmental quality of a lake by sampling from a single site near a point source of pollution, such as an outlet for industrial effluent, then our results will be misleading. To determine the mass of a U. S. penny, our strategy for selecting pennies must ensure that we do not include pennies from other countries.
An awareness of potential sampling errors especially is important when we work with heterogeneous materials. Strategies for obtaining representative samples are covered in Chapter 5.
Method Errors
In any analysis the relationship between the signal, Stotal, and the absolute amount of analyte, nA, or the analyte’s concentration, CA, is
\[S_{total} = k_A n_A + S_{mb} \label{4.3}\]
\[S_{total} = k_A C_A + S_{mb} \label{4.4}\]
where kA is the method’s sensitivity for the analyte and Smb is the signal from the method blank. A method error exists when our value for kA or for Smb is in error. For example, a method in which Stotal is the mass of a precipitate assumes that k is defined by a pure precipitate of known stoichiometry. If this assumption is not true, then the resulting determination of nA or CA is inaccurate. We can minimize a determinate error in kA by calibrating the method. A method error due to an interferent in the reagents is minimized by using a proper method blank.
Measurement Errors
The manufacturers of analytical instruments and equipment, such as glassware and balances, usually provide a statement of the item’s maximum measurement error, or tolerance. For example, a 10-mL volumetric pipet (Figure \(\PageIndex{1}\)) has a tolerance of ±0.02 mL, which means the pipet delivers an actual volume within the range 9.98–10.02 mL at a temperature of 20 oC. Although we express this tolerance as a range, the error is determinate; that is, the pipet’s expected volume, \(\mu\), is a fixed value within this stated range.

Volumetric glassware is categorized into classes based on its relative accuracy. Class A glassware is manufactured to comply with tolerances specified by an agency, such as the National Institute of Standards and Technology or the American Society for Testing and Materials. The tolerance level for Class A glassware is small enough that normally we can use it without calibration. The tolerance levels for Class B glassware usually are twice that for Class A glassware. Other types of volumetric glassware, such as beakers and graduated cylinders, are not used to measure volume accurately. Table \(\PageIndex{1}\) provides a summary of typical measurement errors for Class A volumetric glassware. Tolerances for digital pipets and for balances are provided in Table \(\PageIndex{2}\) and Table \(\PageIndex{3}\).
| Transfer Pipets | Volumetric Flasks | Burets | |||
|---|---|---|---|---|---|
| Capacity (mL) | Tolerance (mL) | Capacity (mL) | Tolerance (mL) | Capacity (mL) | Tolerance (mL) |
| 1 | \(\pm 0.006\) | 5 | \(\pm 0.02\) | 10 | \(\pm 0.02\) |
| 2 | \(\pm 0.006\) | 10 | \(\pm 0.02\) | 25 | \(\pm 0.03\) |
| 5 | \(\pm 0.01\) | 25 | \(\pm 0.03\) | 50 | \(\pm 0.05\) |
| 10 | \(\pm 0.02\) | 50 | \(\pm 0.05\) | ||
| 20 | \(\pm 0.03\) | 100 | \(\pm 0.08\) | ||
| 25 | \(\pm 0.03\) | 250 | \(\pm 0.12\) | ||
| 50 | \(\pm 0.05\) | 500 | \(\pm 0.20\) | ||
| 100 | \(\pm 0.08\) | 1000 | \(\pm 0.30\) | ||
| 2000 | |||||
| Pipet Range | Volume (mL or \(\mu \text{L}\)) | Percent Measurement Error |
|---|---|---|
| 10–100 \(\mu \text{L}\) | 10 | \(\pm 3.0\%\) |
| 50 | \(\pm 1.0\%\) | |
| 100 | \(\pm 0.8\%\) | |
| 100–1000 \(\mu \text{L}\) | 100 | \(\pm 3.0\%\) |
| 500 | \(\pm 1.0\%\) | |
| 1000 | \(\pm 0.6\%\) | |
| 1–10 mL | 1 | \(\pm 3.0\%\) |
| 5 | \(\pm 0.8\%\) | |
| 10 | \(\pm 0.6\%\) |
The tolerance values for the volumetric glassware in Table \(\PageIndex{1}\) are from the ASTM E288, E542, and E694 standards. The measurement errors for the digital pipets in Table \(\PageIndex{2}\) are from www.eppendorf.com.
| Balance | Capacity (g) | Measurement Error |
|---|---|---|
| Precisa 160M | 160 | \(\pm 1 \text{ mg}\) |
| A & D ER 120M | 120 | \(\pm 0.1 \text{ mg}\) |
| Metler H54 | 160 | \(\pm 0.01 \text{ mg}\) |
We can minimize a determinate measurement error by calibrating our equipment. Balances are calibrated using a reference weight whose mass we can trace back to the SI standard kilogram. Volumetric glassware and digital pipets are calibrated by determining the mass of water delivered or contained and using the density of water to calculate the actual volume. It is never safe to assume that a calibration does not change during an analysis or over time. One study, for example, found that repeatedly exposing volumetric glassware to higher temperatures during machine washing and oven drying, led to small, but significant changes in the glassware’s calibration [Castanheira, I.; Batista, E.; Valente, A.; Dias, G.; Mora, M.; Pinto, L.; Costa, H. S. Food Control 2006, 17, 719–726]. Many instruments drift out of calibration over time and may require frequent recalibration during an analysis.
Personal Errors
Finally, analytical work is always subject to personal error, examples of which include the ability to see a change in the color of an indicator that signals the endpoint of a titration, biases, such as consistently overestimating or underestimating the value on an instrument’s readout scale, failing to calibrate instrumentation, and misinterpreting procedural directions. You can minimize personal errors by taking proper care.
Identifying Determinate Errors
Determinate errors often are difficult to detect. Without knowing the expected value for an analysis, the usual situation in any analysis that matters, we often have nothing to which we can compare our experimental result. Nevertheless, there are strategies we can use to detect determinate errors.
The magnitude of a constant determinate error is the same for all samples and is more significant when we analyze smaller samples. Analyzing samples of different sizes, therefore, allows us to detect a constant determinate error. For example, consider a quantitative analysis in which we separate the analyte from its matrix and determine its mass. Let’s assume the sample is 50.0% w/w analyte. As we see in Table \(\PageIndex{4}\), the expected amount of analyte in a 0.100 g sample is 0.050 g. If the analysis has a positive constant determinate error of 0.010 g, then analyzing the sample gives 0.060 g of analyte, or an apparent concentration of 60.0% w/w. As we increase the size of the sample the experimental results become closer to the expected result. An upward or downward trend in a graph of the analyte’s experimental concentration versus the sample’s mass (Figure \(\PageIndex{2}\)) is evidence of a constant determinate error.
| Mass of Sample (g) | Expected Mass of Analyte (g) |
Constant Error (g) | Experimental Mass of Analyte (g) |
Experimental Concentration of Analyte (% w/w) |
|---|---|---|---|---|
| 0.100 | 0.050 | 0.010 | 0.060 | 60.0 |
| 0.200 | 0.100 | 0.010 | 0.110 | 55.0 |
| 0.400 | 0.200 | 0.010 | 0.210 | 52.5 |
| 0.800 | 0.400 | 0.010 | 0.410 | 51.2 |
| 1.600 | 0.800 | 0.010 | 0.810 | 50.6 |

A proportional determinate error, in which the error’s magnitude depends on the amount of sample, is more difficult to detect because the result of the analysis is independent of the amount of sample. Table \(\PageIndex{5}\) outlines an example that shows the effect of a positive proportional error of 1.0% on the analysis of a sample that is 50.0% w/w in analyte. Regardless of the sample’s size, each analysis gives the same result of 50.5% w/w analyte.
| Mass of Sample (g) | Expected Mass of Analyte (g) |
Proportional Error (%) |
Experimental Mass of Analyte (g) |
Experimental Concentration of Analyte (% w/w) |
|---|---|---|---|---|
| 0.100 | 0.050 | 1.00 | 0.0505 | 50.5 |
| 0.200 | 0.100 | 1.00 | 0.101 | 50.5 |
| 0.400 | 0.200 | 1.00 | 0.202 | 50.5 |
| 0.800 | 0.400 | 1.00 | 0.404 | 50.5 |
| 1.600 | 0.800 | 1.00 | 0.808 | 50.5 |
One approach for detecting a proportional determinate error is to analyze a standard that contains a known amount of analyte in a matrix similar to our samples. Standards are available from a variety of sources, such as the National Institute of Standards and Technology (where they are called Standard Reference Materials) or the American Society for Testing and Materials. Table \(\PageIndex{6}\), for example, lists certified values for several analytes in a standard sample of Gingko biloba leaves. Another approach is to compare our analysis to an analysis carried out using an independent analytical method that is known to give accurate results. If the two methods give significantly different results, then a determinate error is the likely cause.
| Class of Analyte | Analyte | Mass Fraction (mg/g or ng/g) |
|---|---|---|
| Flavonoids/Ginkgolide B (mass fraction in mg/g) | Qurecetin | \(2.69 \pm 0.31\) |
| Kaempferol | \(3.02 \pm 0.41\) | |
| Isorhamnetin | \(0.517 \pm 0.0.99\) | |
| Total Aglycones | \(6.22 \pm 0.77\) | |
| Selected Terpenes (mass fraction in mg/g) | Ginkgolide A | \(0.57 \pm 0.28\) |
| Ginkgolide B | \(0.470 \pm 0.090\) | |
| Ginkgolide C | \(0.59 \pm 0.22\) | |
| Ginkgolide J | \(0.18 \pm 0.10\) | |
| Bilobalide | \(1.52 \pm 0.40\) | |
| Total Terpene Lactones | \(3.3 \pm 1.1\) | |
| Selected Toxic Elements (mass fraction in ng/g) | Cadmium | \(20.8 \pm 1.0\) |
| Lead | \(995 \pm 30\) | |
| Mercury | \(23.08 \pm 0.17\) |
The primary purpose of this Standard Reference Material is to validate analytical methods for determining flavonoids, terpene lactones, and toxic elements in Ginkgo biloba or other materials with a similar matrix. Values are from the official Certificate of Analysis available at www.nist.gov.
Constant and proportional determinate errors have distinctly different sources, which we can define in terms of the relationship between the signal and the moles or concentration of analyte (Equation \ref{4.3} and Equation \ref{4.4}). An invalid method blank, Smb, is a constant determinate error as it adds or subtracts the same value to the signal. A poorly calibrated method, which yields an invalid sensitivity for the analyte, kA, results in a proportional determinate error.
Errors that Affect Precision
As we saw in Section 4.1, precision is a measure of the spread of individual measurements or results about a central value, which we express as a range, a standard deviation, or a variance. Here we draw a distinction between two types of precision: repeatability and reproducibility. Repeatability is the precision when a single analyst completes an analysis in a single session using the same solutions, equipment, and instrumentation. Reproducibility, on the other hand, is the precision under any other set of conditions, including between analysts or between laboratory sessions for a single analyst. Since reproducibility includes additional sources of variability, the reproducibility of an analysis cannot be better than its repeatability.
The ratio of the standard deviation associated with reproducibility to the standard deviation associated with repeatability is called the Horowitz ratio. For a wide variety of analytes in foods, for example, the median Horowtiz ratio is 2.0 with larger values for fatty acids and for trace elements; see Thompson, M.; Wood, R. “The ‘Horowitz Ratio’–A Study of the Ratio Between Reproducibility and Repeatability in the Analysis of Foodstuffs,” Anal. Methods, 2015, 7, 375–379.
Errors that affect precision are indeterminate and are characterized by random variations in their magnitude and their direction. Because they are random, positive and negative indeterminate errors tend to cancel, provided that we make a sufficient number of measurements. In such situations the mean and the median largely are unaffected by the precision of the analysis.
Sources of Indeterminate Error
We can assign indeterminate errors to several sources, including collecting samples, manipulating samples during the analysis, and making measurements. When we collect a sample, for instance, only a small portion of the available material is taken, which increases the chance that small-scale inhomogeneities in the sample will affect repeatability. Individual pennies, for example, may show variations in mass from several sources, including the manufacturing process and the loss of small amounts of metal or the addition of dirt during circulation. These variations are sources of indeterminate sampling errors.
During an analysis there are many opportunities to introduce indeterminate method errors. If our method for determining the mass of a penny includes directions for cleaning them of dirt, then we must be careful to treat each penny in the same way. Cleaning some pennies more vigorously than others might introduce an indeterminate method error.
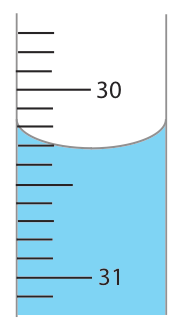
Finally, all measuring devices are subject to indeterminate measurement errors due to limitations in our ability to read its scale. For example, a buret with scale divisions every 0.1 mL has an inherent indeterminate error of ±0.01–0.03 mL when we estimate the volume to the hundredth of a milliliter (Figure \(\PageIndex{3}\)).
Evaluating Indeterminate Error
Indeterminate errors associated with our analytical equipment or instrumentation generally are easy to estimate if we measure the standard deviation for several replicate measurements, or if we monitor the signal’s fluctuations over time in the absence of analyte (Figure \(\PageIndex{4}\)) and calculate the standard deviation. Other sources of indeterminate error, such as treating samples inconsistently, are more difficult to estimate.

To evaluate the effect of an indeterminate measurement error on our analysis of the mass of a circulating United States penny, we might make several determinations of the mass for a single penny (Table \(\PageIndex{7}\)). The standard deviation for our original experiment (see Table 4.1.1) is 0.051 g, and it is 0.0024 g for the data in Table \(\PageIndex{7}\). The significantly better precision when we determine the mass of a single penny suggests that the precision of our analysis is not limited by the balance. A more likely source of indeterminate error is a variability in the masses of individual pennies.
| Replicate | Mass (g) | Replicate | Mass (g) |
|---|---|---|---|
| 1 | 3.025 | 6 | 3.023 |
| 2 | 3.024 | 7 | 3.022 |
| 3 | 3.028 | 8 | 3.021 |
| 4 | 3.027 | 9 | 3.026 |
| 5 | 3.028 | 10 | 3.024 |
In Section 4.5 we will discuss a statistical method—the F-test—that you can use to show that this difference is significant.
Error and Uncertainty
Analytical chemists make a distinction between error and uncertainty [Ellison, S.; Wegscheider, W.; Williams, A. Anal. Chem. 1997, 69, 607A–613A]. Error is the difference between a single measurement or result and its expected value. In other words, error is a measure of bias. As discussed earlier, we divide errors into determinate and indeterminate sources. Although we can find and correct a source of determinate error, the indeterminate portion of the error remains.
Uncertainty expresses the range of possible values for a measurement or result. Note that this definition of uncertainty is not the same as our definition of precision. We calculate precision from our experimental data and use it to estimate the magnitude of indeterminate errors. Uncertainty accounts for all errors—both determinate and indeterminate—that reasonably might affect a measurement or a result. Although we always try to correct determinate errors before we begin an analysis, the correction itself is subject to uncertainty.
Here is an example to help illustrate the difference between precision and uncertainty. Suppose you purchase a 10-mL Class A pipet from a laboratory supply company and use it without any additional calibration. The pipet’s tolerance of ±0.02 mL is its uncertainty because your best estimate of its expected volume is 10.00 mL ± 0.02 mL. This uncertainty primarily is determinate. If you use the pipet to dispense several replicate samples of a solution and determine the volume of each sample, the resulting standard deviation is the pipet’s precision. Table \(\PageIndex{8}\) shows results for ten such trials, with a mean of 9.992 mL and a standard deviation of ±0.006 mL. This standard deviation is the precision with which we expect to deliver a solution using a Class A 10-mL pipet. In this case the pipet’s published uncertainty of ±0.02 mL is worse than its experimentally determined precision of ±0.006 ml. Interestingly, the data in Table \(\PageIndex{8}\) allows us to calibrate this specific pipet’s delivery volume as 9.992 mL. If we use this volume as a better estimate of the pipet’s expected volume, then its uncertainty is ±0.006 mL. As expected, calibrating the pipet allows us to decrease its uncertainty [Kadis, R. Talanta 2004, 64, 167–173].
| Replicate | Volume (ml) | Replicate | Volume (mL) |
|---|---|---|---|
| 1 | 10.002 | 6 | 9.983 |
| 2 | 9.993 | 7 | 9.991 |
| 3 | 9.984 | 8 | 9.990 |
| 4 | 9.996 | 9 | 9.988 |
| 5 | 9.989 | 10 | 9.999 |


