3.6: Energetics of Chemical Reactions - An Introduction

In the previous section we posed the following question: "The First Law tells us that energy is not created during chemical reactions, so the obvious question becomes: in what form is that energy, that which ends up as precious heat, before the combustion takes place?"

 

 

 

Figure 3-15. According to the First Law of Thermodynamics, the energy released during combustion is not created by the reaction between the fuel (wax) and oxygen. It must have existed prior to burning, but in what form? ("Candle flame (88/365)" by SilverStack is licensed under CC BY-NC 2.0. )

 

 

With an understanding of chemical potential energy in place, we can return to the question of combustion, referred to as “The Mystery of Fire” by Michael Faraday [17]. Where does the heat released upon the burning of a fuel come from? The First Law of Thermodynamics tells us in no uncertain terms that the energy must exist in some form before the burning begins. It seems to be hidden in the fuel somehow, waiting to be released. Let’s do a little thought experiment to shed some light on this puzzle, beginning with the following reaction, the burning of hydrogen gas to make water. This is the same reaction that produced the fireball at the tail end of the Hindenburg seen in Figure 3-1 at the beginning of this chapter.

\[ \ce{2 H2 (g) +  O2 (g)  -> 2 H2O (g)} \]

According to the above equation, the hydrogen begins as H₂ molecules, with each hydrogen atom connected by a hydrogen-hydrogen bond as described in the preceding section; two atoms of oxygen are similarly joined together in molecules of O₂ by an oxygen-oxygen bond [18]. As we discussed, atoms so connected can be separated by performing work on them, that is, by pulling them apart. The energy required in these cases are as follows: each mole of H₂ molecule requires 436 kJ of work to separate the hydrogen atoms, while each mole of O₂ requires the input of 498 kJ of work to separate the molecules into their component atoms. If we start with two moles of H₂ and one mole of O₂, we would increase the potential energy of this collection of six moles of atoms (we would have four moles of H and two moles of O) by 1370 kJ. We won’t worry about exactly how we would perform such work; at this point, focus on the quantity of work and energy (which can be interconverted and therefore can be expressed using the same units). 

The above process is illustrated on the left of Figure 3-16; diagrams of this sort, called energy diagrams, can be constructed for any chemical reaction and can be useful to visualize the relevant energetic changes. If those six moles of atoms were to recombine with their original partners, thereby regenerating two moles of H₂ and one mole of O₂, their potential energy would simply decrease by 1370 kJ, bringing it right back to where it started. The system would be indistinguishable from what it was at the start and no net heat or energy would be evolved [19]. But what if they were to combine to form two molecules of H₂O instead? The O-H bond is quite strong, and each one that forms decreases the potential energy of the atoms by an average of 0.77 aJ per bond, or 463 kJ/mol; by making four moles of such bonds (each mole of H₂O has two moles of OH bonds), the potential energy decreases by 1852 kJ, as shown on the right side of Figure 3-16. This decrease brings the potential energy possessed by the atoms to a lower level than it started. And because energy is not destroyed, that decrease in potential energy must manifest in a converted form of energy — heat. To summarize, while we had to “invest” 1370 kJ to break the bonds of the molecules we started with, the eventual decrease in potential energy was greater in magnitude and the difference, the potential energy lost (labeled ΔE), results in the generation of heat [20]. Reactions such as this, where heat is evolved due to an decrease in the chemical potential energy, are called exothermic. Most spontaneous reactions are exothermic, but not all of them. Some reactions convert heat from their surroundings; these are called endothermic. 

 

 

Figure 3-16. An energy diagram illustrating the changes in potential energy involved in splitting H₂ and O₂ molecules and then “reassembling” them as two molecules of H₂O; there is a net loss of 482 kJ/mol in potential energy for the process and that “loss” is manifested as heat.

---

How realistic is the above analysis? Do chemical reactions really work that way. Good questions. There are two very different answers to them. No, chemical reactions do not work by splitting all of the molecules into component atoms and then reassembling them. In many cases, only a fragment or two of a larger molecule is involved, with most of the molecule remaining intact. Even in a case like the combustion of octane, where the fuel really is completely disassembled, it does not proceed by splitting all of the atoms apart before reassembling them. It is much messier than that, with many intermediate species generated and consumed along the way. But the mathematical analysis — the calculation of the energy changes — is highly accurate, provided that the relevant bond strengths are known with precision (which is, unfortunately, frequently the case, as the example below explains). In this particular example, because the bond energies are quite accurate, the resulting calculation of ΔE is also very close to the experimentally observed value.

To summarize, the collection of particles involved in a combustion reaction, electrons and various atomic nuclei, can rearrange in such a way to decrease their potential energy by breaking weak bonds and then forming stronger ones. In terms of the potential energy well approach, atoms crawl their way out of relatively shallow potential energy wells and then fall down deeper ones, ending up with a lower potential energy than they started with. The heat realized by burning fuels is not created energy, but merely potential energy that has been transformed. 

The above argument lays out a sort of accounting scheme of energy and is useful because any energetic transformation is, according to the First Law, a zero-sum game; the total energy of the system must be the same before and after the reaction. But such accounting does not provide any insight into why two molecules of water should have a lower potential energy, that is to say, greater stability, than two molecules of H₂ and one of O₂. While certain of the details of the explanation require a more sophisticated understanding of electronic structure than we have laid out thus far, we can provide the following conceptual insights. 

As you probably suspect, because these are atoms, which consist of oppositely charged protons and electrons, the energetic interactions are primarily electrostatic in nature. The electrons that form the H₂ bond are shared equally by two identical hydrogen nuclei. But the electrons that form each OH bond are shared unequally by the hydrogen and oxygen nuclei, with the electrons being closer to the oxygen nucleus; because of the particulars of the electronic structure of oxygen, an important aspect of which is the much higher nuclear charge (it has eight protons), the electrons that originated in H₂, in effect, gain access to a greater positive charge by bonding with oxygen. This lowers their potential energy compared to electrons that must settle for the meager nuclear charge of being near only hydrogen nuclei. It is the stronger attraction of the oxygen nuclei toward the electrons in the hydrogen that ultimately provides the reduction of the chemical potential energy. For all intents and purposes, the electrons that originated in the H-H bond fall into a new, deeper energy well by forming bonds with oxygen; the system as a whole loses potential energy as a result. 

The energetics of all combustion reactions, indeed all chemical reactions, can be similarly analyzed. We can generalize the approach used above by writing the following expression:

\[ \Delta\ E = \sum BE_{bonds\ broken} - \sum BE_{bonds\ formed} \]

The above notation means that the sum of bond energies (BE) of all the bonds that are formed is subtracted from the sum of all the bonds that are formed. Some common bond energies are presented in Table 3-2; these are the values that are typical for the combustion of alkanes, alkenes, alcohols, and carboxylic acids. To illustrate how to use the above relationship, we calculate the heat released from the combustion of propane below.

Table 3-2. Average Bond Energies for Selected Single Bonds, A-B, and Double Bonds A=B (in kJ/mol)
Single Bonds
	Element A
		C	H	O
Element B	C	346	413	358
	H	-	436	463
	O	-	-	146
Common Double Bonds	O=O	498	C=C	610
	C=O	745

 

Example

Problem 3.9 Estimate the heat released by the complete combustion of 1 mole of propane gas.

Solution

The general idea is the same as we employed for burning H₂, but the fuel is a more complex structure. Start with the balanced chemical reaction describing the reaction:

\[ \ce{C3H8 (g) + 5 O2 (g)  -> 4 H2O (g) + 3 CO2 (g)} \nonumber \]

It is helpful here to generate a list of all the bonds that are broken and formed in the reaction. To do so, we need a bit more information on the structure of carbon dioxide. For reasons that we discuss later, CO₂ has two C=O double bonds (recall from Chapter 1 that this arrangement satisfies carbon's normal valence of four and oxygen's valence of two). All of the C-C and C-H bonds in propane and the two O-H bonds in water are all single bonds. We can now list the bonds broken and formed:

• Bonds Broken: 3 C-C bonds, 8 C-H bonds and 5 O=O bonds
• Bonds Formed: 8 O-H bonds and 6 C=O bonds

We calculate the energy balance by subtracting the potential energy released upon formation of the new bonds from the sum of the energy required to break all of the bonds of the initial molecules, or, 

\[ \begin{align*}
\Delta\ E &= \sum BE_{bonds\ broken} - \sum BE_{bonds\ formed} \\[5pt]
&= [3\ BE_{C-C}\ + 8\ BE_{C-H}\ + 5\ BE_{O=O}] - [6\ BE_{C=O}\ + 8\ BE_{O-H}] \\[5pt]
&=[3(346) + 8(413) + 5(498) ]\  \mbox{kJ mol}^{-1}-[6(745)+8(463)]\  \mbox{kJ mol}^{-1}\\[5pt]
&=5794\   \mbox{kJ mol}^{-1} - 8174\  \mbox{kJ mol}^{-1}\\[5pt]
&=-2380\  \mbox{kJ mol}^{-1}
\end{align*} \] 

This calculation indicates that roughly 2400 kJ of energy is released upon the combustion of one mole of propane. Why? Potential energy is lost in this transformation because the electrons that initially comprised the bonds of the propane and oxygen molecules end up closer to positive charges than they started, as we also saw in the formation of water above. The chemical potential energy is therefore lowered and the "lost" energy is converted to heat. That explains the logic of the negative sign in the answer; the atoms lost energy and therefore fall deeper into an energy well. A positive result would mean that the atoms would have gained potential energy and, therefore, rather than releasing heat to their surroundings (as all combustion reactions do), heat would have been absorbed, making the surroundings colder rather than hotter.

How accurate is the above? You may have noticed that the phrasing of the question was to "estimate" the heat released upon combustion of propane. When these calculations are based on "average bond energies", as was true here, there will always be a certain degree of error. Bond energies depend on subtle structural features of molecules and can vary by as much as 10% from the average values in Table 3-2. Compounding the problem is the fact that we need to find the difference between two relatively large numbers, each of which is subject to error. As such, calculations such as these provide good estimates of energy changes, but if more accuracy is needed more refined approaches and/or more accurate bond energy data is necessary. In this case, the experimentally determined energy change has been shown to be -2219 kJ mol-1, so our estimate above was off by -161 kJ/mol, or by about -7%. 

The approach followed in the previous examples can be extended to reactions that are not combustion reactions. In Chapter 1, we introduced a few important reactions that involved changes in functional groups, primarily those involving double bonds. Recall that alkenes can be converted to alcohols via the addition of water, or hydration (Figure 3-17).

---

Figure 3-17. The hydration of hex-3-ene to hexan-3-ol. The exo- or endothermicity of the hydration of alkenes can be estimated using bond energies.

---

 

Example 

Problem 3.10 Estimate the change in chemical potential energy associated with the addition of water to hex-3-ene, shown in Figure 3-17. Is the process exothermic or endothermic?

Solution

To estimate the energy change for a reaction such as this, we need only consider the strengths of the bonds that are either formed or broken. You can see that the carbon backbone remains largely intact, so most of the C-C and C-H bonds that exist in the starting compound are also present in the product. The bonds that change are:

• The bonds that are broken are:
  • 1 C=C bond
  • 1 O-H bond
• The bonds that are formed are:
  • 1 C-C bond
  • 1 C-O bond
  • 1 C-H bond

Using the bond strengths listed in Table 3-2, we estimate the energy change in the reaction as follows:

\[ \begin{align*}
\Delta\ E &= \sum BE_{bonds\ broken} - \sum BE_{bonds\ formed} \\[5pt]
&= [BE_{C=C}\ + BE_{O-H}] - [BE_{C-C}\ +BE_{C-H}\ + BE_{C-O}] \\[5pt]
&=[(610) + (463)]\  \mbox{kJ mol}^{-1}-[(346)+(413)+(358)]\  \mbox{kJ mol}^{-1}\\[5pt]
&=1073\   \mbox{kJ mol}^{-1} - 1117\  \mbox{kJ mol}^{-1}\\[5pt]
&=-44\  \mbox{kJ mol}^{-1}
\end{align*} \] 

How to think about the above result? First, you should notice that the magnitude of the energy change is much smaller than that for the combustion reactions we have considered to this point. It is very mildly exothermic, but close enough to being energetically neutral — meaning that there is little energetic difference between reactants and products — that you might suspect that the reaction can proceed in either direction. This is, in fact, exactly right. Alkenes can be converted to alcohols via addition of water (hydration), and alcohols can be converted to alkenes via the elimination of water (dehydration). How accurate is the above calculation? Not bad. Experimental data indicates that the change in energy is -55 kJ mol^-1, in line with the estimate above.

 

Exercise

Problem 3.11 Using the approach employed above, estimate the energy change for the hydrogenation of hex-3-ene, as illustrated below. Is the process exothermic or endothermic?

 

---

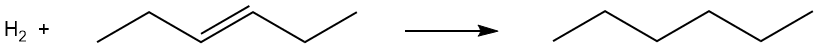
Notes and References.

[17] Michael Faraday, inventor of the world’s first electric motor, was an unlikely giant in both chemistry and physics. The youngest of thirteen children, his father was sentenced to debtor’s prison when he was young. Apprenticed to a bookbinder, his passion for science grew after coming across a chemistry text. A collection of his popular lectures, entitled The Chemical History of a Candle, is still available and is highly recommended. 

[18] As we will see in Chapter 4, this is a double bond, but the nature of the bond does not affect the argument here.

[19] Gotcha! Wouldn’t this violate the Second Law of Thermodynamics?!? Why yes, yes it would, provided it were to take place exactly as described. In reality we would have to expend more than 1370 kJ to break apart the molecules into their component atoms because whatever process would might use, it wouldn't be completely efficient.

[20] So much heat that, on a mass basis, there is no more energy rich fuel than hydrogen gas, a fact that has given rise to much speculation about an eventual “hydrogen economy”; in addition to yielding a large amount of energy, burning hydrogen produces only water, no carbon-containing greenhouse gases.