9.5: Metallic Bonding
- Page ID
- 98644
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)A third major type of chemical bonding is metallic bonding. Whereas ionic bonds join metals to non-metals and covalent bonds join non-metals to each other, metallic bonding joins a bulk of metal atoms. A metallic substance may be a pure element (e.g. aluminum foil, copper wires), or it may be a mixture of two or more elements in an alloy (e.g. brass instruments, "white gold" jewelry). Metals tend to have high melting points and boiling points suggesting strong bonds between the atoms. Even a soft metal like sodium (melting point 97.8°C) melts at a considerably higher temperature than the element (neon) which precedes it in the Periodic Table. However, unlike ionic compounds, metals are usually malleable rather than brittle, suggesting that they do not form a rigid lattice structure of oppositely charged ions; neither do metals form bonded molecules like covalent compounds, however. A different model of bonding is necessary to explain the properties of metallic substances. In the 1900's, Paul Drüde came up with the "sea of electrons" metallic bonding theory by modeling metals as a mixture of atomic cores (atomic cores = positive nuclei + inner shell of electrons) and valence electrons.
The Electron Sea Model
Consider sodium metal as an example. Sodium has the electronic structure 1s22s22p63s1. When sodium atoms come together, the electron in the 3s atomic orbital of one sodium atom can share space with the corresponding electron on a neighboring atom to form a bond - in much the same sort of way that a covalent bond is formed. The difference, however, is that each sodium atom is being touched by eight other sodium atoms - and the sharing occurs between the central atom and the 3s orbitals on all of the eight other atoms. Each of these eight is in turn being touched by eight sodium atoms, which in turn are touched by eight atoms - and so on and so on, until you have taken in all the atoms in that lump of sodium. All of the 3s electrons on all of the atoms are shared in nondirectional bonds which extend over the whole piece of metal. The electrons can move freely within the lump of metal, and so each electron becomes detached from its parent atom. The electrons are said to be delocalized. The metal is held together by the strong forces of attraction between the positive nuclei and the delocalized electrons (Figure \(\PageIndex{1}\)).
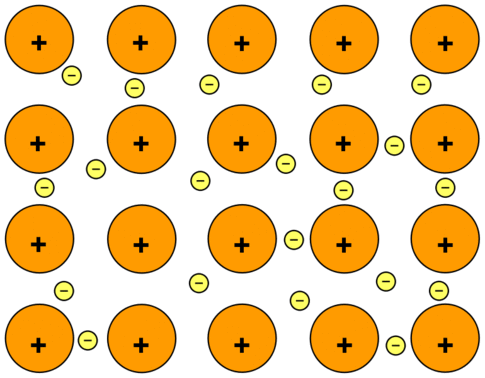
Figure \(\PageIndex{1}\): Metallic Bonding: The Electron Sea Model: Positive atomic nuclei (orange circles) surrounded by a sea of delocalized electrons (yellow circles).
This is sometimes described as "an array of positive ions in a sea of electrons". If you are going to use this view, beware! Is a metal made up of atoms or ions? It is made of atoms. Each positive center in the diagram represents all the rest of the atom apart from the outer electron, but that electron has not been lost - it may no longer have an attachment to a particular atom, but it's still there in the structure. Sodium metal is therefore written as \(\ce{Na}\), not \(\ce{Na^+}\).
In a molten metal, the metallic bonding is still present, although the ordered structure has been broken down. The metallic bond is not fully broken until the metal boils. That means that boiling point is actually a better guide to the strength of the metallic bond than melting point is. On melting, the bond is loosened, not broken. The strength of a metallic bond depends on three things:
- The number of electrons that become delocalized from the metal
- The charge of the cation (metal).
- The size of the cation.
A strong metallic bond will be the result of more delocalized electrons, which causes the effective nuclear charge on electrons on the cation to increase, in effect making the size of the cation smaller. Metallic bonds are strong and require a great deal of energy to break, and therefore metals have high melting and boiling points. A metallic bonding theory must explain how so much bonding can occur with such few electrons (since metals are located on the left side of the periodic table and do not have many electrons in their valence shells). The theory must also account for all of a metal's unique chemical and physical properties.
Example \(\PageIndex{1}\): Metallic bonding in magnesium
Use the sea of electrons model to explain why magnesium has a higher melting point (650 °C) than sodium (97.79 °C).
Solution
If you work through the same argument above for sodium with magnesium, you end up with stronger bonds and hence a higher melting point.
Magnesium has the outer electronic structure 3s2. Both of these electrons become delocalized, so the "sea" has twice the electron density as it does in sodium. The remaining "ions" also have twice the charge (if you are going to use this particular view of the metal bond) and so there will be more attraction between "ions" and "sea".
More realistically, each magnesium atom has 12 protons in the nucleus compared with sodium's 11. In both cases, the nucleus is screened from the delocalized electrons by the same number of inner electrons - the 10 electrons in the 1s2 2s2 2p6 orbitals. That means that there will be a net pull from the magnesium nucleus of 2+, but only 1+ from the sodium nucleus.
So not only will there be a greater number of delocalized electrons in magnesium, but there will also be a greater attraction for them from the magnesium nuclei. Magnesium atoms also have a slightly smaller radius than sodium atoms, and so the delocalized electrons are closer to the nuclei. Each magnesium atom also has twelve near neighbors rather than sodium's eight. Both of these factors increase the strength of the bond still further.
Note: Transition metals tend to have particularly high melting points and boiling points. The reason is that they can involve the 3d electrons in the delocalization as well as the 4s. The more electrons you can involve, the stronger the attractions tend to be.
Bulk Properties of Metals
Metals have several qualities that are unique, such as the ability to conduct electricity and heat, a low ionization energy, and a low electronegativity (so they will give up electrons easily to form cations). Their physical properties include a lustrous (shiny) appearance, and they are malleable and ductile. Metals have a crystal structure but can be easily deformed. In the electron sea model, the valence electrons are free, delocalized, mobile, and not associated with any particular atom. This model may account for:
- Conductivity: Since the electrons are free, if electrons from an outside source were pushed into a metal wire at one end (Figure \(\PageIndex{2}\)), the electrons would move through the wire and come out at the other end at the same rate. Since conductivity is the movement of charge through a material, it follows that metals will be able to conduct electricity efficiently.

Figure \(\PageIndex{2}\): The "sea of electrons" is free to flow about the crystal of positive metal ions. These flowing electron can conduct electrical change when an electric field is applied (e.g., a battery). Image used with permission (CC-BY-SA; OpenStax and Rafaelgarcia).
- Malleability and Ductility: The electron-sea model of metals not only explains their electrical properties but their malleability and ductility as well. The sea of electrons surrounding the protons acts like a cushion, and so when the metal is hammered on, for instance, the overall composition of the structure of the metal is not harmed or changed. The protons may be rearranged but the sea of electrons with adjust to the new formation of protons and keep the metal intact. When one layer of ions in an electron sea moves along one space with respect to the layer below it, the crystal structure does not fracture (like an ionic crystal would) but is only deformed (Figure \(\PageIndex{3}\)).

Figure \(\PageIndex{3}\): Malleability of metals originate from each of moving layer of atoms with respect to each other. The final situation is much the same as the initial. Thus if we hit a metal with a hammer, the crystals do not shatter, but merely change their shape.
- Heat capacity: This is explained by the ability of free electrons to move about the solid. As they move, they efficiently transfer heat (that is, kinetic energy) through the material.
- Luster: The free electrons can absorb photons of light in the "sea," so metals are opaque-looking. However, electrons on the surface can bounce back light at the same frequency that the light hits the surface, therefore the metal appears to be shiny.
These observations are only qualitative, and not quantitative, so they are difficult to verify experimentally. The "Sea of Electrons" theory stands today only as an oversimplified model of how metallic bonding works, but it is a sufficient first approximation.
In the first section of this chapter, we argued that models of chemical bonding are idealized concepts and the reality can often be somewhere "in between". While many compounds can be unambiguously identified as "ionic", "covalent", or "metallic", there are other possibilities. Compounds may be polar covalent, having both properties of covalent and ionic bonds; other materials may be semimetallic, such as many semiconductors. Understanding the simplified models helps guide our thinking when we encounter such substances that seem to defy classification.
Contributors
Jim Clark (Chemguide.co.uk)
- Daniel James Berger
- Wikipedia
Ed Vitz (Kutztown University), John W. Moore (UW-Madison), Justin Shorb (Hope College), Xavier Prat-Resina (University of Minnesota Rochester), Tim Wendorff, and Adam Hahn.
- Anna Christianson (Bellarmine University)

