2.1: Polar Covalent Bonds- Electronegativity
- Page ID
- 67052
After completing this section, you should be able to
- describe how differences in electronegativity give rise to bond polarity.
- arrange a given series of the elements most often encountered in organic chemistry (C, H, O, S, P and the halogens) in order of increasing or decreasing electronegativity, without referring to a table of electronegativities.
- predict the positive and negative ends of a given bond formed between any two of the elements listed in Objective 2, above, without the use of a table of electronegativities or a periodic table.
- predict the positive and negative ends of a given bond formed between any two elements not listed in Objective 2, above, using a periodic table.
Make certain that you can define, and use in context, the key terms below.
- electronegativity inductive effect
- polar colvalent bond
Students often wonder why it is important to be able to tell whether a given bond is polar or not, and why they need to know which atoms carry a partial positive charge and which a partial negative charge. Consider the chloromethane (CH3Cl) molecule. The carbon atom is shown as carrying a partial positive charge. Now, recall that opposite charges attract. Thus, it seems reasonable that the slightly positive carbon atom in chloromethane should be susceptible to attack by a negatively charged species, such as the hydroxide ion, OH−. This theory is borne out in practice: hydroxide ions react with chloromethane by attacking the slightly positive carbon atom in the latter. It is often possible to rationalize chemical reactions in this manner, and you will find the knowledge of bond polarity indispensible when you start to write reaction mechanisms. Note: Because of the small difference in electronegativity between carbon and hydrogen, the $\ce{\sf{C-H}}$ bond is normally assumed to be nonpolar.
Electronegativity
The elements with the highest ionization energies are generally those with the most negative electron affinities, which are located toward the upper right corner of the periodic table. Conversely, the elements with the lowest ionization energies are generally those with the least negative electron affinities and are located in the lower left corner of the periodic table.
Because the tendency of an element to gain or lose electrons is so important in determining its chemistry, various methods have been developed to quantitatively describe this tendency. The most important method uses a measurement called electronegativity (represented by the Greek letter chi, χ, pronounced “ky” as in “sky”), defined as the relative ability of an atom to attract electrons to itself in a chemical compound. Elements with high electronegativities tend to acquire electrons in chemical reactions and are found in the upper right corner of the periodic table. Elements with low electronegativities tend to lose electrons in chemical reactions and are found in the lower left corner of the periodic table.
Unlike ionization energy or electron affinity, the electronegativity of an atom is not a simple, fixed property that can be directly measured in a single experiment. In fact, an atom’s electronegativity should depend to some extent on its chemical environment because the properties of an atom are influenced by its neighbors in a chemical compound. Nevertheless, when different methods for measuring the electronegativity of an atom are compared, they all tend to assign similar relative values to a given element. For example, all scales predict that fluorine has the highest electronegativity and cesium the lowest of the stable elements, which suggests that all the methods are measuring the same fundamental property.
Electronegativity is defined as the ability of an atom in a particular molecule to attract electrons to itself. The greater the value, the greater the attractiveness for electrons.
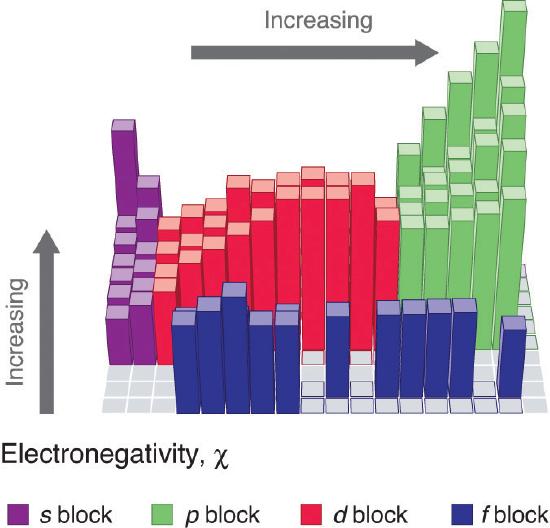
Unfortunately there is no direct way of measuring electronegativity. Dipole-moment measurements tell us about the electrical behavior of all electron pairs in the molecule, not just the bonding pair in which we are interested. Also, the polarity of a bond depends on whether the bond is a single, double, or triple bond and on what the other atoms and electron pairs in a molecule are. Therefore the dipole moment cannot tell us quantitatively the difference between the electronegativities of two bonded atoms. Various attempts have been made over the years to derive a scale of electronegativities for the elements, none of which is entirely satisfactory. Nevertheless most of these attempts agree in large measure in telling us which elements are more electronegative than others. The best-known of these scales was devised by the Nobel prize-winning California chemist Linus Pauling (1901 to 1994) and is shown in the periodic table found below. In this scale a value of 4.0 is arbitrarily given to the most electronegative element, fluorine, and the other electronegativities are scaled relative to this value.
What if two atoms of equal electronegativity bond together?
Consider a bond between two atoms, A and B. If the atoms are equally electronegative, both have the same tendency to attract the bonding pair of electrons, and so it will be found on average half way between the two atoms:
To get a bond like this, A and B would usually have to be the same atom. You will find this sort of bond in, for example, H2 or Cl2 molecules. Note: It's important to realize that this is an average picture. The electrons are actually in a molecular orbital, and are moving around all the time within that orbital. This sort of bond could be thought of as being a "pure" covalent bond - where the electrons are shared evenly between the two atoms.
What if B is slightly more electronegative than A?
B will attract the electron pair rather more than A does.
That means that the B end of the bond has more than its fair share of electron density and so becomes slightly negative. At the same time, the A end (rather short of electrons) becomes slightly positive. In the diagram, "\(\delta\)" (read as "delta") means "slightly" - so \(\delta+\) means "slightly positive".
A polar bond is a covalent bond in which there is a separation of charge between one end and the other - in other words in which one end is slightly positive and the other slightly negative. Examples include most covalent bonds. The hydrogen-chlorine bond in HCl or the hydrogen-oxygen bonds in water are typical.
If B is a lot more electronegative than A, then the electron pair is dragged right over to B's end of the bond. To all intents and purposes, A has lost control of its electron, and B has complete control over both electrons. Ions have been formed. The bond is then an ionic bond rather than a covalent bond.
A "spectrum" of bonds
The implication of all this is that there is no clear-cut division between covalent and ionic bonds. In a pure covalent bond, the electrons are held on average exactly half way between the atoms. In a polar bond, the electrons have been dragged slightly towards one end. How far does this dragging have to go before the bond counts as ionic? There is no real answer to that. Sodium chloride is typiclly considered an ionic solid, but even here the sodium has not completely lost control of its electron. Because of the properties of sodium chloride, however, we tend to count it as if it were purely ionic. Lithium iodide, on the other hand, would be described as being "ionic with some covalent character". In this case, the pair of electrons has not moved entirely over to the iodine end of the bond. Lithium iodide, for example, dissolves in organic solvents like ethanol - not something which ionic substances normally do.
Figure \(\PageIndex{3}\): The Electron Distribution in a Nonpolar Covalent Bond, a Polar Covalent Bond, and an Ionic Bond Using Lewis Electron Structures. Electron-rich (negatively charged) regions are shown in blue; electron-poor (positively charged) regions are shown in red.
In a simple diatomic molecule like HBr, if the bond is polar, then the whole molecule is polar. What about more complicated molecules?
Figure: (left) CCl4 (right) CHCl3
Consider CCl4, (left panel in figure above), which as a molecule is not polar - in the sense that it doesn't have an end (or a side) which is slightly negative and one which is slightly positive. The whole of the outside of the molecule is somewhat negative, but there is no overall separation of charge from top to bottom, or from left to right.
In contrast, CHCl3 is a polar molecule (right panel in figure above). The hydrogen at the top of the molecule is less electronegative than carbon and so is slightly positive. This means that the molecule now has a slightly positive "top" and a slightly negative "bottom", and so is overall a polar molecule.
A polar molecule will need to be "lop-sided" in some way.
Summary
Covalent bonds form when electrons are shared between atoms and are attracted by the nuclei of both atoms. In pure covalent bonds, the electrons are shared equally. In polar covalent bonds, the electrons are shared unequally, as one atom exerts a stronger force of attraction on the electrons than the other. The ability of an atom to attract a pair of electrons in a chemical bond is called its electronegativity. The difference in electronegativity between two atoms determines how polar a bond will be. In a diatomic molecule with two identical atoms, there is no difference in electronegativity, so the bond is nonpolar or pure covalent. When the electronegativity difference is very large, as is the case between metals and nonmetals, the bonding is characterized as ionic.
- No electronegativity difference between two atoms leads to a non-polar covalent bond.
- A small electronegativity difference leads to a polar covalent bond.
- A large electronegativity difference leads to an ionic bond.
Exercises
- Identify the positive and negative ends of each of the bonds shown below.

- Which of the following elements is the more electronegative?
a) Br or C
b) C or H
c) Cl or I
d) C or Li
3. Which of the following molecules would you expect to have the more polarized O-H bond?
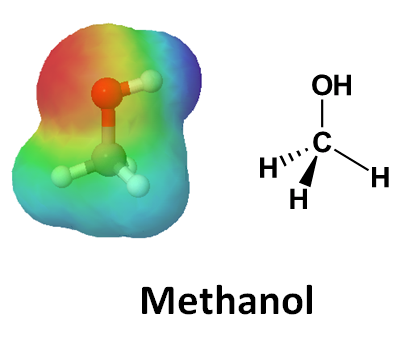
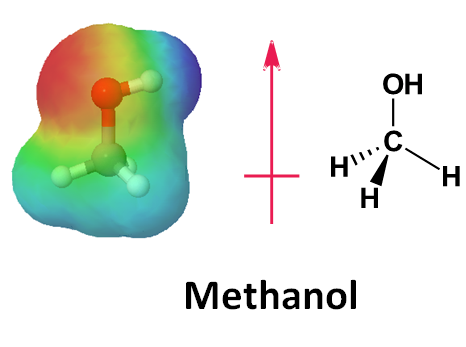
4. Predict the direction of polarizing C-O bond in methanol by looking at its electrostatic potential map.
Solutions
a) Br
b) C
c) Cl
d) C
3.
The molecule on the right would have the more polorized O-H bond. The presence of the highly electronegative fluorines would draw electrons away by the inductive effect.
4.
Contributors
Dr. Dietmar Kennepohl FCIC (Professor of Chemistry, Athabasca University)
Prof. Steven Farmer (Sonoma State University)
Organic Chemistry With a Biological Emphasis by Tim Soderberg (University of Minnesota, Morris)
Ed Vitz (Kutztown University), John W. Moore (UW-Madison), Justin Shorb (Hope College), Xavier Prat-Resina (University of Minnesota Rochester), Tim Wendorff, and Adam Hahn.
Jim Clark (Chemguide.co.uk)

