12.2: Interpreting Mass Spectra
- Page ID
- 67278
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Objectives
After completing this section, you should be able to
- suggest possible molecular formulas for a compound, given the m/z value for the molecular ion, or a mass spectrum from which this value can be obtained.
- predict the relative heights of the M+·, (M + 1)+·, etc., peaks in the mass spectrum of a compound, given the natural abundance of the isotopes of carbon and the other elements present in the compound.
- interpret the fragmentation pattern of the mass spectrum of a relatively simple, known compound (e.g., hexane).
- use the fragmentation pattern in a given mass spectrum to assist in the identification of a relatively simple, unknown compound (e.g., an unknown alkane).
When interpreting fragmentation patterns, you may find it helpful to know that, as you might expect, the weakest carbon-carbon bonds are the ones most likely to break. You might wish to refer to the table of bond dissociation energies when attempting problems involving the interpretation of mass spectra.
This page looks at how fragmentation patterns are formed when organic molecules are fed into a mass spectrometer, and how you can get information from the mass spectrum.
The Origin of Fragmentation Patterns
When the vaporized organic sample passes into the ionization chamber of a mass spectrometer, it is bombarded by a stream of electrons. These electrons have a high enough energy to knock an electron off an organic molecule to form a positive ion. This ion is called the molecular ion - or sometimes the parent ion and is often given the symbol M+ or . The dot in this second version represents the fact that somewhere in the ion there will be a single unpaired electron. That's one half of what was originally a pair of electrons - the other half is the electron which was removed in the ionization process.
The molecular ions are energetically unstable, and some of them will break up into smaller pieces. The simplest case is that a molecular ion breaks into two parts - one of which is another positive ion, and the other is an uncharged free radical.
The uncharged free radical will not produce a line on the mass spectrum. Only charged particles will be accelerated, deflected and detected by the mass spectrometer. These uncharged particles will simply get lost in the machine - eventually, they get removed by the vacuum pump.
The ion, X+, will travel through the mass spectrometer just like any other positive ion - and will produce a line on the stick diagram. All sorts of fragmentations of the original molecular ion are possible - and that means that you will get a whole host of lines in the mass spectrum. For example, the mass spectrum of pentane looks like this:
The pattern of lines in the mass spectrum of an organic compound tells you something quite different from the pattern of lines in the mass spectrum of an element. With an element, each line represents a different isotope of that element. With a compound, each line represents a different fragment produced when the molecular ion breaks up.
In the stick diagram showing the mass spectrum of pentane, the line produced by the heaviest ion passing through the machine (at m/z = 72) is due to the molecular ion. The tallest line in the stick diagram (in this case at m/z = 43) is called the base peak. This is usually given an arbitrary height of 100, and the height of everything else is measured relative to this. The base peak is the tallest peak because it represents the commonest fragment ion to be formed - either because there are several ways in which it could be produced during fragmentation of the parent ion, or because it is a particularly stable ion.
Using Fragmentation Patterns
This section will ignore the information you can get from the molecular ion (or ions). That is covered in three other pages which you can get at via the mass spectrometry menu. You will find a link at the bottom of the page.
Let's have another look at the mass spectrum for pentane:
What causes the line at m/z = 57?
How many carbon atoms are there in this ion? There cannot be 5 because 5 x 12 = 60. What about 4? 4 x 12 = 48. That leaves 9 to make up a total of 57. How about C4H9+ then?
C4H9+ would be [CH3CH2CH2CH2]+, and this would be produced by the following fragmentation:
The methyl radical produced will simply get lost in the machine.
The line at m/z = 43 can be worked out similarly. If you play around with the numbers, you will find that this corresponds to a break producing a 3-carbon ion:
The line at m/z = 29 is typical of an ethyl ion, [CH3CH2]+:
The other lines in the mass spectrum are more difficult to explain. For example, lines with m/z values 1 or 2 less than one of the easy lines are often due to loss of one or more hydrogen atoms during the fragmentation process.
This time the base peak (the tallest peak - and so the commonest fragment ion) is at m/z = 57. But this is not produced by the same ion as the same m/z value peak in pentane.
If you remember, the m/z = 57 peak in pentane was produced by [CH3CH2CH2CH2]+. If you look at the structure of pentan-3-one, it's impossible to get that particular fragment from it.
Work along the molecule mentally chopping bits off until you come up with something that adds up to 57. With a small amount of patience, you'll eventually find [CH3CH2CO]+ - which is produced by this fragmentation:
You would get exactly the same products whichever side of the CO group you split the molecular ion. The m/z = 29 peak is produced by the ethyl ion - which once again could be formed by splitting the molecular ion either side of the CO group.
Peak Heights and Stability
The more stable an ion is, the more likely it is to form. The more of a particular sort of ion that's formed, the higher its peak height will be. We'll look at two common examples of this.
Carbocations (carbonium ions)
Summarizing the most important conclusion from the page on carbocations:
Order of stability of carbocations
primary < secondary < tertiary
Applying the logic of this to fragmentation patterns, it means that a split which produces a secondary carbocation is going to be more successful than one producing a primary one. A split producing a tertiary carbocation will be more successful still. Let's look at the mass spectrum of 2-methylbutane. 2-methylbutane is an isomer of pentane - isomers are molecules with the same molecular formula, but a different spatial arrangement of the atoms.
Look first at the very strong peak at m/z = 43. This is caused by a different ion than the corresponding peak in the pentane mass spectrum. This peak in 2-methylbutane is caused by:
The ion formed is a secondary carbocation - it has two alkyl groups attached to the carbon with the positive charge. As such, it is relatively stable. The peak at m/z = 57 is much taller than the corresponding line in pentane. Again a secondary carbocation is formed - this time, by:
You would get the same ion, of course, if the left-hand CH3 group broke off instead of the bottom one as we've drawn it. In these two spectra, this is probably the most dramatic example of the extra stability of a secondary carbocation.
Acylium ions, [RCO]+
Ions with the positive charge on the carbon of a carbonyl group, C=O, are also relatively stable. This is fairly clearly seen in the mass spectra of ketones like pentan-3-one.
The base peak, at m/z=57, is due to the [CH3CH2CO]+ ion. We've already discussed the fragmentation that produces this.
The more stable an ion is, the more likely it is to form. The more of a particular ion that is formed, the higher will be its peak height.
Using mass spectra to distinguish between compounds
Suppose you had to suggest a way of distinguishing between pentan-2-one and pentan-3-one using their mass spectra.
| pentan-2-one | CH3COCH2CH2CH3 | |
| pentan-3-one | CH3CH2COCH2CH3 |
Each of these is likely to split to produce ions with a positive charge on the CO group. In the pentan-2-one case, there are two different ions like this:
- [CH3CO]+
- [COCH2CH2CH3]+
That would give you strong lines at m/z = 43 and 71. With pentan-3-one, you would only get one ion of this kind:
- [CH3CH2CO]+
In that case, you would get a strong line at 57. You don't need to worry about the other lines in the spectra - the 43, 57 and 71 lines give you plenty of difference between the two. The 43 and 71 lines are missing from the pentan-3-one spectrum, and the 57 line is missing from the pentan-2-one one.
The two mass spectra look like this:
As you've seen, the mass spectrum of even very similar organic compounds will be quite different because of the different fragmentation patterns that can occur. Provided you have a computer data base of mass spectra, any unknown spectrum can be computer analyzed and simply matched against the data base.
Exercise
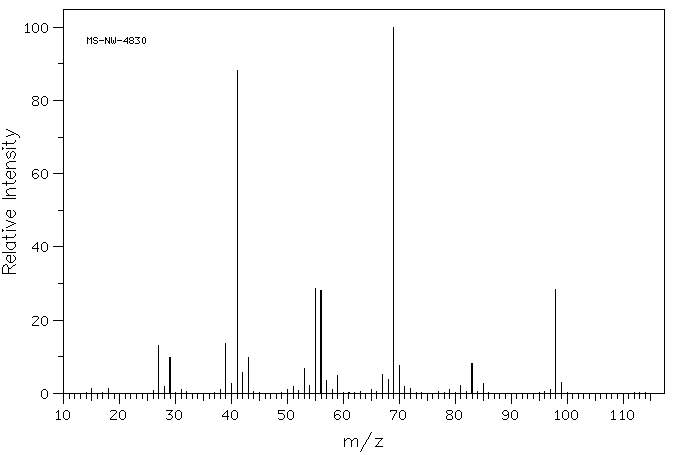
The following are the spectrum for 2-methyl-2-hexene and 2-heptene, which spectra belongs to the correct molecule. Explain.
A
B
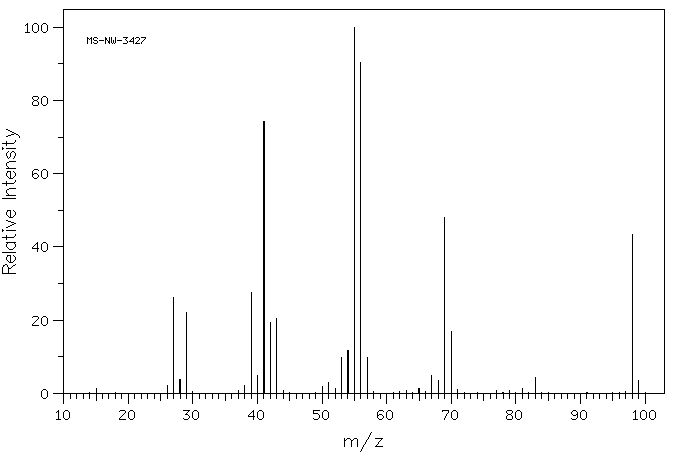.gif?revision=1&size=bestfit&width=579&height=390)
- Answer
-
Spectrum A is the 2-methyl-2-hexene and the Spectrum B is is 2-heptene.
Looking at A the peak at 68 m/z is the fractioned molecule with just the tri-substituted alkene present. While B has a strong peak around the 56 m/z, which in this case is the di-substituted alkene left behind from the linear heptene.
Contributors and Attributions
Dr. Dietmar Kennepohl FCIC (Professor of Chemistry, Athabasca University)
Prof. Steven Farmer (Sonoma State University)
Organic Chemistry With a Biological Emphasis by Tim Soderberg (University of Minnesota, Morris)
Jim Clark (Chemguide.co.uk)

