7.9: Carbocation Structure and Stability
- Page ID
- 67130
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)After completing this section, you should be able to
- describe the geometry of a given carbocation.
- arrange a given series of carbocations in order of increasing or decreasing stability.
- explain the relative stability of methyl, primary, secondary and tertiary carbocations in terms of hyperconjugation and inductive effects.
Although hyperconjugation can be used to explain the relative stabilities of carbocations, this explanation is certainly not the only one, and is by no means universally accepted. A more common explanation, involving the concept of an inductive effect, is given below.
It is a general principle in chemistry that the more a charge is dispersed, the more stable is the species carrying the charge. Put simply, a species in which a positive charge is shared between two atoms would be more stable than a similar species in which the charge is borne wholly by a single atom. In a tertiary carbocation, the positively charged carbon atom attracts the bonding electrons in the three carbon-carbon sigma (σ) bonds, and thus creates slight positive charges on the carbon atoms of the three surrounding alkyl groups (and, indeed, on the hydrogen atoms attached to them). Chemists sometimes use an arrow to represent this inductive release:
Note: These diagrams do not reflect the geometry of the carbocation. The overall charge on the carbocation remains unchanged, but some of the charge is now carried by the alkyl groups attached to the central carbon atom; that is, the charge has been dispersed.
In the tertiary carbocation shown above, the three alkyl groups help to stabilize the positive charge. In a secondary carbocation, only two alkyl groups would be available for this purpose, while a primary carbocation has only one alkyl group available. Thus the observed order of stability for carbocations is as follows:
tertiary > secondary > primary > methyl.
Stability of carbocation intermediates
We know that the rate-limiting step of an SN1 reaction is the first step - formation of the this carbocation intermediate. The rate of this step – and therefore, the rate of the overall substitution reaction – depends on the activation energy for the process in which the bond between the carbon and the leaving group breaks and a carbocation forms. According to Hammond’s postulate (section 6.2B), the more stable the carbocation intermediate is, the faster this first bond-breaking step will occur. In other words, the likelihood of a nucleophilic substitution reaction proceeding by a dissociative (SN1) mechanism depends to a large degree on the stability of the carbocation intermediate that forms.
The critical question now becomes, what stabilizes a carbocation?
So if it takes an electron withdrawing group to stabilize a negative charge, what will stabilize a positive charge? An electron donating group!
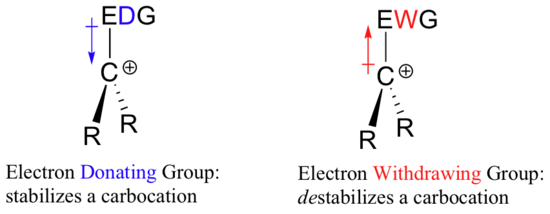
A positively charged species such as a carbocation is very electron-poor, and thus anything which donates electron density to the center of electron poverty will help to stabilize it. Conversely, a carbocation will be destabilized by an electron withdrawing group.
Alkyl groups – methyl, ethyl, and the like – are weak electron donating groups, and thus stabilize nearby carbocations. What this means is that, in general, more substituted carbocations are more stable: a tert-butyl carbocation, for example, is more stable than an isopropyl carbocation. Primary carbocations are highly unstable and not often observed as reaction intermediates; methyl carbocations are even less stable.
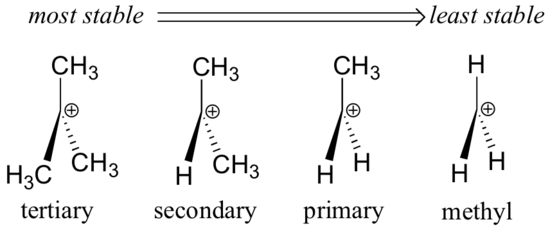
Alkyl groups are electron donating and carbocation-stabilizing because the electrons around the neighboring carbons are drawn towards the nearby positive charge, thus slightly reducing the electron poverty of the positively-charged carbon.
It is not accurate to say, however, that carbocations with higher substitution are always more stable than those with less substitution. Just as electron-donating groups can stabilize a carbocation, electron-withdrawing groups act to destabilize carbocations. Carbonyl groups are electron-withdrawing by inductive effects, due to the polarity of the C=O double bond. It is possible to demonstrate in the laboratory (see section 16.1D) that carbocation A below is more stable than carbocation B, even though A is a primary carbocation and B is secondary.
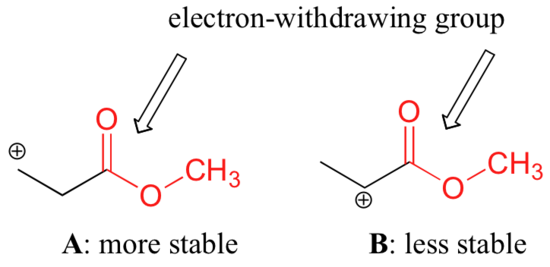
The difference in stability can be explained by considering the electron-withdrawing inductive effect of the ester carbonyl. Recall that inductive effects - whether electron-withdrawing or donating - are relayed through covalent bonds and that the strength of the effect decreases rapidly as the number of intermediary bonds increases. In other words, the effect decreases with distance. In species B the positive charge is closer to the carbonyl group, thus the destabilizing electron-withdrawing effect is stronger than it is in species A.
In the next chapter we will see how the carbocation-destabilizing effect of electron-withdrawing fluorine substituents can be used in experiments designed to address the question of whether a biochemical nucleophilic substitution reaction is SN1 or SN2.
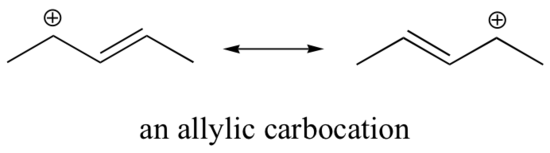
Stabilization of a carbocation can also occur through resonance effects, and as we have already discussed in the acid-base chapter, resonance effects as a rule are more powerful than inductive effects. Consider the simple case of a benzylic carbocation:

This carbocation is comparatively stable. In this case, electron donation is a resonance effect. Three additional resonance structures can be drawn for this carbocation in which the positive charge is located on one of three aromatic carbons. The positive charge is not isolated on the benzylic carbon, rather it is delocalized around the aromatic structure: this delocalization of charge results in significant stabilization. As a result, benzylic and allylic carbocations (where the positively charged carbon is conjugated to one or more non-aromatic double bonds) are significantly more stable than even tertiary alkyl carbocations.
Because heteroatoms such as oxygen and nitrogen are more electronegative than carbon, you might expect that they would by definition be electron withdrawing groups that destabilize carbocations. In fact, the opposite is often true: if the oxygen or nitrogen atom is in the correct position, the overall effect is carbocation stabilization. This is due to the fact that although these heteroatoms are electron withdrawing groups by induction, they are electron donating groups by resonance, and it is this resonance effect which is more powerful. (We previously encountered this same idea when considering the relative acidity and basicity of phenols and aromatic amines in section 7.4). Consider the two pairs of carbocation species below:
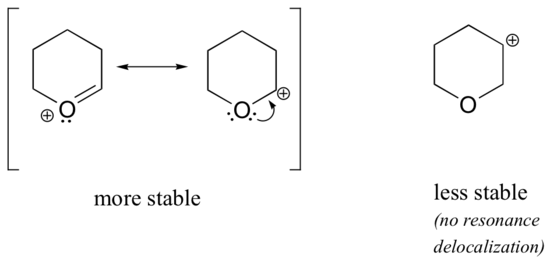
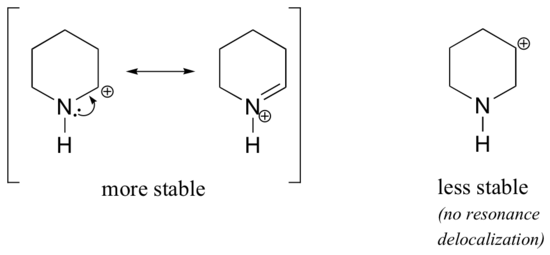
In the more stable carbocations, the heteroatom acts as an electron donating group by resonance: in effect, the lone pair on the heteroatom is available to delocalize the positive charge. In the less stable carbocations the positively-charged carbon is more than one bond away from the heteroatom, and thus no resonance effects are possible. In fact, in these carbocation species the heteroatoms actually destabilize the positive charge, because they are electron withdrawing by induction.
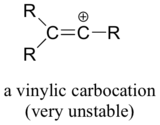
Finally, vinylic carbocations, in which the positive charge resides on a double-bonded carbon, are very unstable and thus unlikely to form as intermediates in any reaction.
In which of the structures below is the carbocation expected to be more stable? Explain.
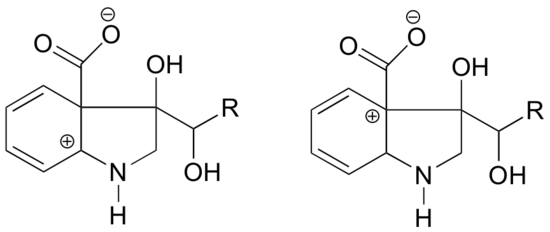
- Answer
-
In the carbocation on the left, the positive charge is located in a position relative to the nitrogen such that the lone pair of electrons on the nitrogen can be donated to fill the empty orbital. This is not possible for the carbocation species on the right.
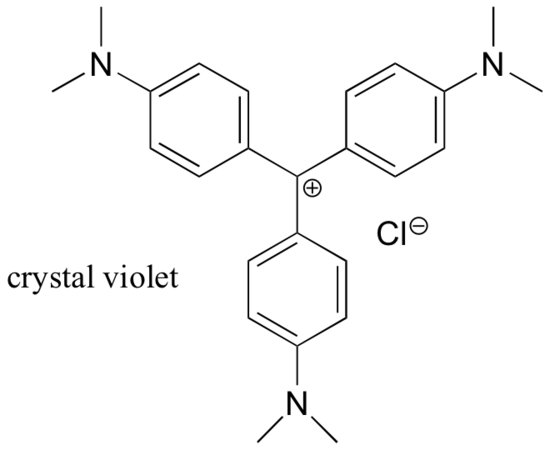
For the most part, carbocations are very high-energy, transient intermediate species in organic reactions. However, there are some unusual examples of very stable carbocations that take the form of organic salts. Crystal violet is the common name for the chloride salt of the carbocation whose structure is shown below. Notice the structural possibilities for extensive resonance delocalization of the positive charge, and the presence of three electron-donating amine groups.
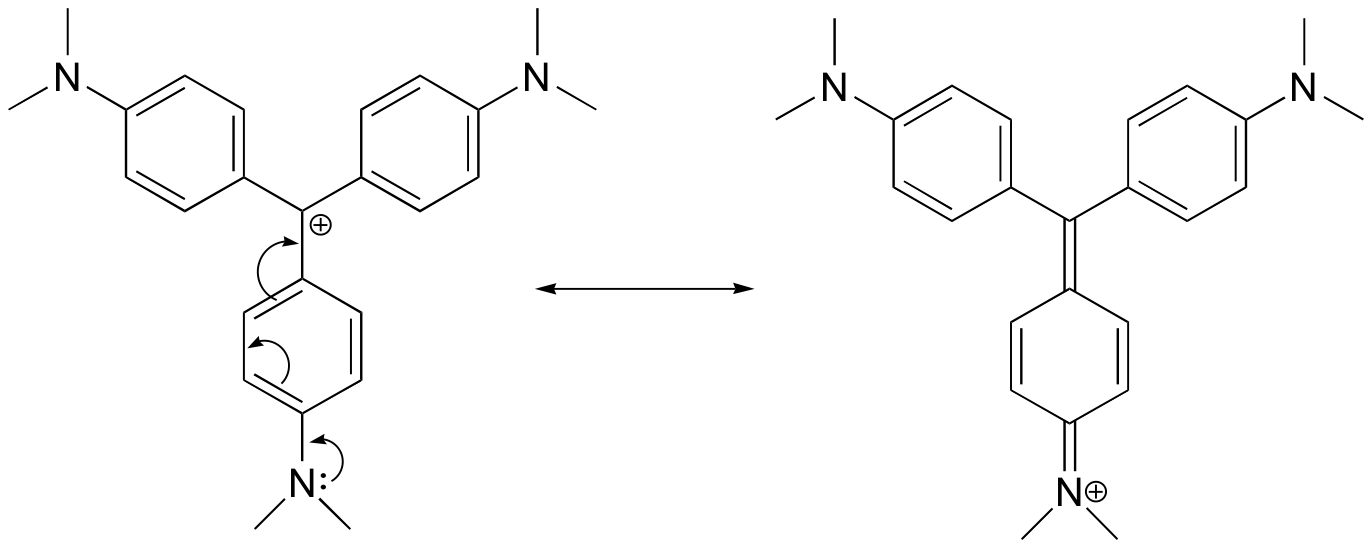
Draw a resonance structure of the crystal violet cation in which the positive charge is delocalized to one of the nitrogen atoms.
- Answer
When considering the possibility that a nucleophilic substitution reaction proceeds via an SN1 pathway, it is critical to evaluate the stability of the hypothetical carbocation intermediate. If this intermediate is not sufficiently stable, an SN1 mechanism must be considered unlikely, and the reaction probably proceeds by an SN2 mechanism. In the next chapter we will see several examples of biologically important SN1 reactions in which the positively charged intermediate is stabilized by inductive and resonance effects inherent in its own molecular structure.
State which carbocation in each pair below is more stable, or if they are expected to be approximately equal. Explain your reasoning.
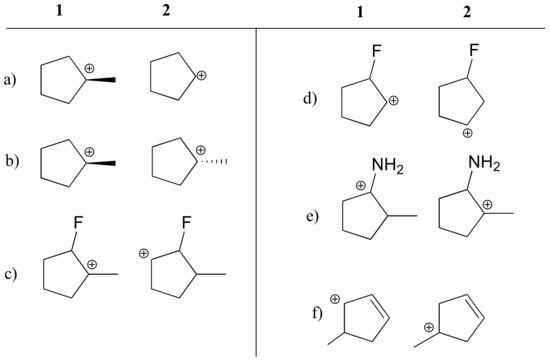
- Answer
-
a) 1 (tertiary vs. secondary carbocation)
b) equal
c) 1 (tertiary vs. secondary carbocation)
d) 2 (positive charge is further from electron-withdrawing fluorine)
e) 1 (lone pair on nitrogen can donate electrons by resonance)
f) 1 (allylic carbocation – positive charge can be delocalized to a second carbon)
Exercise
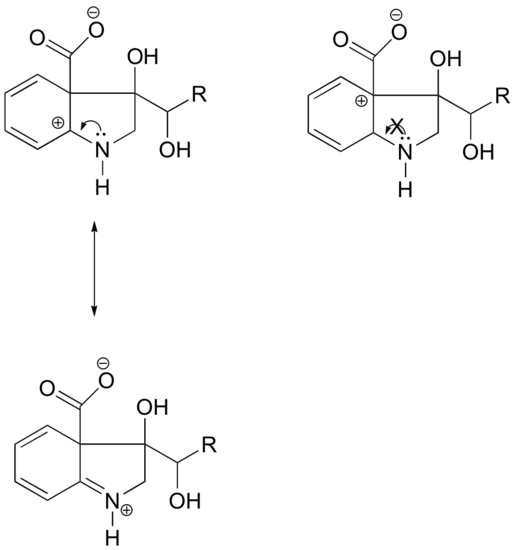
Draw the cationic intermediates that are seen in the following reactions.
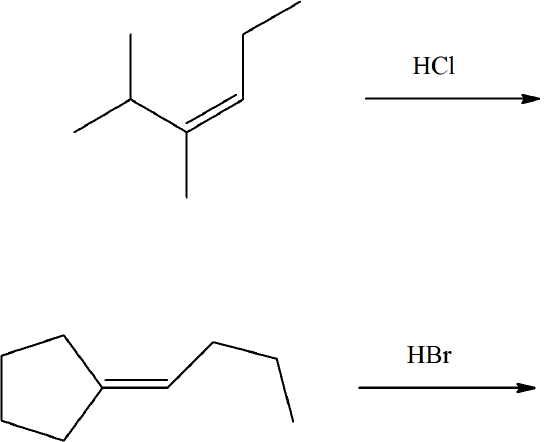
- Answer
-
Contributors and Attributions
Dr. Dietmar Kennepohl FCIC (Professor of Chemistry, Athabasca University)
Prof. Steven Farmer (Sonoma State University)
Organic Chemistry With a Biological Emphasis by Tim Soderberg (University of Minnesota, Morris)

