Learning Objectives
- Use molarity to determine quantities in chemical reactions.
- Use molarity as a conversion factor in calculations.
Another way of expressing concentration is to give the number of moles of solute per unit volume of solution. Of all the quantitative measures of concentration, molarity is the one used most frequently by chemists. Molarity is defined as the number of moles of solute per liter of solution.
\[\mathrm{molarity=\dfrac{number\: of\: moles\: of\: solute}{number\: of\: liters\: of\: solution}} \label{defMolarity} \]
The symbol for molarity is \(\text{M}\) or moles/liter. Chemists also use square brackets to indicate a reference to the molarity of a substance. For example, the expression \(\left[ \ce{Ag^+} \right]\) refers to the molarity of the silver ion in solution. Solution concentrations expressed in molarity are the easiest to perform calculations with, but the most difficult to make in the lab. Such concentration units are useful for discussing chemical reactions in which a solute is a product or a reactant. Molar mass can then be used as a conversion factor to convert amounts in moles to amounts in grams.
It is important to remember that “mol” in this expression refers to moles of solute and that “L” refers to liters of solution. For example, if you have 1.5 mol of NaCl dissolved in 0.500 L of solution, its molarity is
\[\mathrm{\dfrac{1.5\: mol\: NaCl}{0.500\: L\: solution}=3.0\: M\: NaCl} \nonumber \]
Sometimes (aq) is added when the solvent is water, as in “3.0 M NaCl (aq).” This is read as "a 3.00 molar sodium chloride solution," meaning that there are 3.00 moles of NaOH dissolved per one liter of solution.
Be sure to note that molarity is calculated as the total volume of the entire solution, not just volume of solvent! The solute contributes to total volume.
If the quantity of the solute is given in mass units, you must convert mass units to mole units before using the definition of molarity to calculate concentration. For example, what is the molar concentration of a solution of 22.4 g of HCl dissolved in 1.56 L?
Step 1: First, convert the mass of solute to moles using the molar mass of HCl (36.5 g/mol):
\[22.4\cancel{gHCl}\times \dfrac{1\: mol\: HCl}{36.5\cancel{gHCl}}=0.614\, mol\; HCl \nonumber \]
Step 2: Now we can use the definition of molarity to determine a concentration:
\[M \: =\: \dfrac{0.614\: mol\: HCl}{1.56L\: solution}=0.394\, M HCl \nonumber \]
Before a molarity concentration can be calculated, the amount of the solute must be expressed in moles, and the volume of the solution must be expressed in liters, as demonstrated in the following example.
Example \(\PageIndex{1}\)
A solution is prepared by dissolving \(42.23 \: \text{g}\) of \(\ce{NH_4Cl}\) into enough water to make \(500.0 \: \text{mL}\) of solution. Calculate its molarity.
Solution
Solutions to Example 13.6.1
| Steps for Problem Solving |
|
| Identify the "given" information and what the problem is asking you to "find." |
Given:
Mass \(= 42.23 \: \text{g} \: \ce{NH_4Cl}\)
Volume solution \(= 500.0 \: \text{mL} = 0.5000 \: \text{L}\)
Find: Molarity = ? M
|
| List other known quantities. |
Molar mass \(\ce{NH_4Cl} = 53.50 \: \text{g/mol}\) |
| Plan the problem. |
1. The mass of the ammonium chloride is first converted to moles.
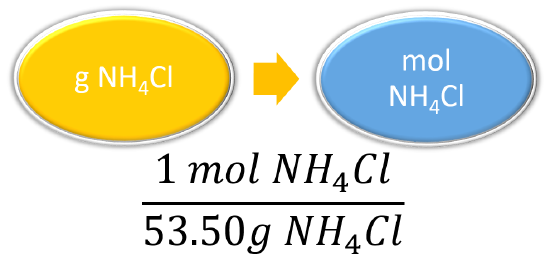
2. Then the molarity is calculated by dividing by liters. Note the given volume has been converted to liters.
\(\mathrm{M=\dfrac{mol\: NH_4Cl}{L\: solution}} \)
|
| Cancel units and calculate. |
Now substitute the known quantities into the equation and solve.
\(\begin{align*} 42.23 \ \cancel{\text{g} \: \ce{NH_4Cl}} \times \dfrac{1 \: \text{mol} \: \ce{NH_4Cl}}{53.50 \: \cancel{\text{g} \: \ce{NH_4Cl}}} &= 0.7893 \: \text{mol} \: \ce{NH_4Cl} \\ \dfrac{0.7893 \: \text{mol} \: \ce{NH_4Cl}}{0.5000 \: \text{L solution}} &= 1.579 \: \text{M} \end{align*}\)
|
| Think about your result. |
The molarity is \(1.579 \: \text{M}\), meaning that a liter of the solution would contain \(1.579 \: \text{mol} \: \ce{NH_4Cl}\). Four significant figures are appropriate. |
Exercise \(\PageIndex{1A}\)
What is the molarity of a solution made when 66.2 g of C6H12O6 are dissolved to make 235 mL of solution?
- Answer
-
1.57 M C6H12O6
Exercise \(\PageIndex{1B}\)
What is the concentration, in \(\text{mol/L}\), where \(137 \: \text{g}\) of \(\ce{NaCl}\) has been dissolved in enough water to make \(500 \: \text{mL}\) of solution?
- Answer
-
4.69 M NaCl
Using Molarity in Calculations
Concentration can be a conversion factor between the amount of solute and the amount of solution or solvent (depending on the definition of the concentration unit). As such, concentrations can be useful in a variety of stoichiometry problems. In many cases, it is best to use the original definition of the concentration unit; it is that definition that provides the conversion factor.
A simple example of using a concentration unit as a conversion factor is one in which we use the definition of the concentration unit and rearrange; we can do the calculation again as a unit conversion, rather than as a definition.
Example \(\PageIndex{2}\): Determining Moles of Solute, Given the Concentration and Volume of a Solution
For example, suppose we ask how many moles of solute are present in 0.108 L of a 0.887 M NaCl solution. Because 0.887 M means 0.887 mol/L, we can use this second expression for the concentration as a conversion factor:
Solution
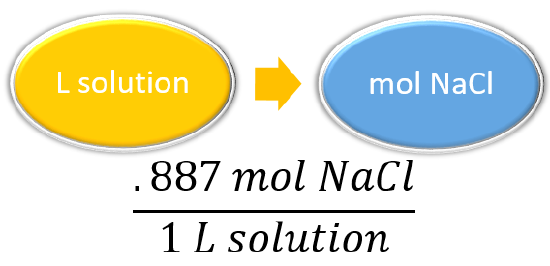
\[0.108\cancel{L\, solution}\times \dfrac{0.887\, mol\, NaCl}{\cancel{1L\, solution}}=0.0958\, mol\, NaCl \nonumber \]
If we used the definition approach, we get the same answer, but now we are using conversion factor skills.
Like any other conversion factor that relates two different types of units, the reciprocal of the concentration can be also used as a conversion factor.
Example \(\PageIndex{3}\): Determining Volume of a Solution, Given the Concentration and Moles of Solute
Using concentration as a conversion factor, how many liters of 2.35 M CuSO4 are needed to obtain 4.88 mol of CuSO4?
Solution
This is a one-step conversion, but the concentration must be written as the reciprocal for the units to work out:
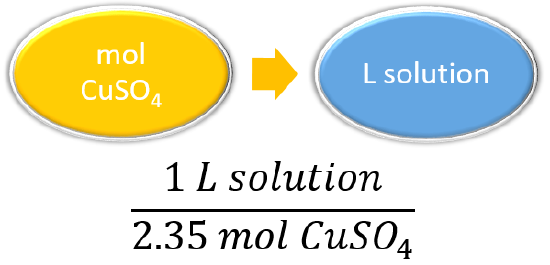
\[4.88\cancel{mol\, CuSO_{4}}\times \dfrac{1\, L\, solution}{2.35\cancel{mol\, CuSO_{4}}}=2.08\, L\, of \, solution \nonumber \]
In a laboratory situation, a chemist must frequently prepare a given volume of solutions of a known molarity. The task is to calculate the mass of the solute that is necessary. The molarity equation can be rearranged to solve for moles, which can then be converted to grams. The following example illustrates this.
Example \(\PageIndex{4}\)
A chemist needs to prepare \(3.00 \: \text{L}\) of a \(0.250 \: \text{M}\) solution of potassium permanganate \(\left( \ce{KMnO_4} \right)\). What mass of \(\ce{KMnO_4}\) does she need to make the solution?
Solution
Solutions to Example 13.6.4
| Steps for Problem Solving |
|
| Identify the "given" information and what the problem is asking you to "find." |
Given:
Molarity \(= 0.250 \: \text{M}\)
Volume \(= 3.00 \: \text{L}\)
Find: Mass \(\ce{KMnO_4} = ? \: \text{g}\)
|
| List other known quantities. |
Molar mass \(\ce{KMnO_4} = 158.04 \: \text{g/mol}\)
0.250 mol KMnO4 to 1 L of KMnO4 solution
|
| Plan the problem. |
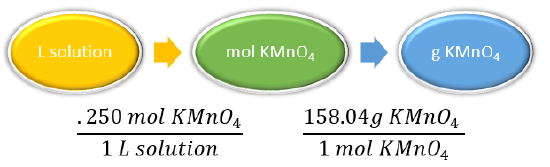 |
| Cancel units and calculate. |
Now substitute the known quantities into the equation and solve.
\(\begin{align*} \text{mol} \: \ce{KMnO_4} = 0.250 \: \text{M} \: \ce{KMnO_4} \times 3.00 \: \text{L} &= 0.750 \: \text{mol} \: \ce{KMnO_4} \\ \cancel{3.00 \: L \: solution} \times \dfrac{0.250 \: \cancel{\text{mol} \: \ce{KMnO_4}}}{1\cancel{L \: solution}} \times \dfrac{158.04 \: \text{g} \: \ce{KMnO_4}}{1 \: \cancel{\text{mol} \: \ce{KMnO_4}}} &= 119 \: \text{g} \: \ce{KMnO_4} \end{align*}\)
|
| Think about your result. |
When \(119 \: \text{g}\) of potassium permanganate is dissolved into water to make \(3.00 \: \text{L}\) of solution, the molarity is \(0.250 \: \text{M}\). |
Exercise \(\PageIndex{4A}\)
Using concentration as a conversion factor, how many liters of 0.0444 M CH2O are needed to obtain 0.0773 mol of CH2O?
- Answer
-
1.74 L
Exercise \(\PageIndex{4B}\)
Answer the problems below using concentration as a conversion factor.
- What mass of solute is present in 1.08 L of 0.0578 M H2SO4?
- What volume of 1.50 M HCl solution contains 10.0 g of hydrogen chloride?
- Answer a
-
6.12 g
- Answer b
-
183 mL or 0.183L
How to Indicate Concentration
- Square brackets are often used to represent concentration, e.g., [NaOH] = 0.50 M.
- Use the capital letter M for molarity, not a lower case m (this is a different concentration unit called molality).
Watch as the Flinn Scientific Tech Staff demonstrates "How To Prepare Solutions."
It is important to note that there are many different ways you can set up and solve your chemistry equations. Some students prefer to answer multi-step calculations in one long step, while others prefer to work out each step individually. Neither method is necessarily better or worse than the other method—whichever makes the most sense to you is the one that you should use. In this text, we will typically use unit analysis (also called dimension analysis or factor analysis).
Contributors and Attributions

