14.7: Solution Dilution
- Page ID
- 289458
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Learning Objectives
- Explain how concentrations can be changed in the lab.
- Understand how stock solutions are used in the laboratory.
Muriatic acid, another name for HCl (aq), is widely used for cleaning concrete and masonry surfaces (see Figure \(\PageIndex{1}\)). The acid must be diluted before use to get it down to a safer strength. Commercially available at concentrations of about 18%, muriatic acid may be used to remove scales and deposits (usually composed of basic materials).
Stock Solutions
It is often necessary to have a solution with a concentration that is very precisely known. A solution containing a precise mass of solute in a precise volume of solution is called a stock solution (or standard solution). A volumetric flask is usually used to prepare a stock solution. Aliquots (carefully measured volumes) of the stock solution can then be diluted to any desired volume. In other cases, it may be inconvenient to weigh a small mass of sample accurately enough to prepare a small volume of a dilute solution. Instead, a more concentrated solution is first prepared. An aliquot of this solution is then diluted to the desired concentration.
Dilutions
When additional water is added to an aqueous solution, the concentration of that solution decreases. This is because the amount of solute remains the same, while the volume of the solution increases (see Figure \(\PageIndex{2}\)).
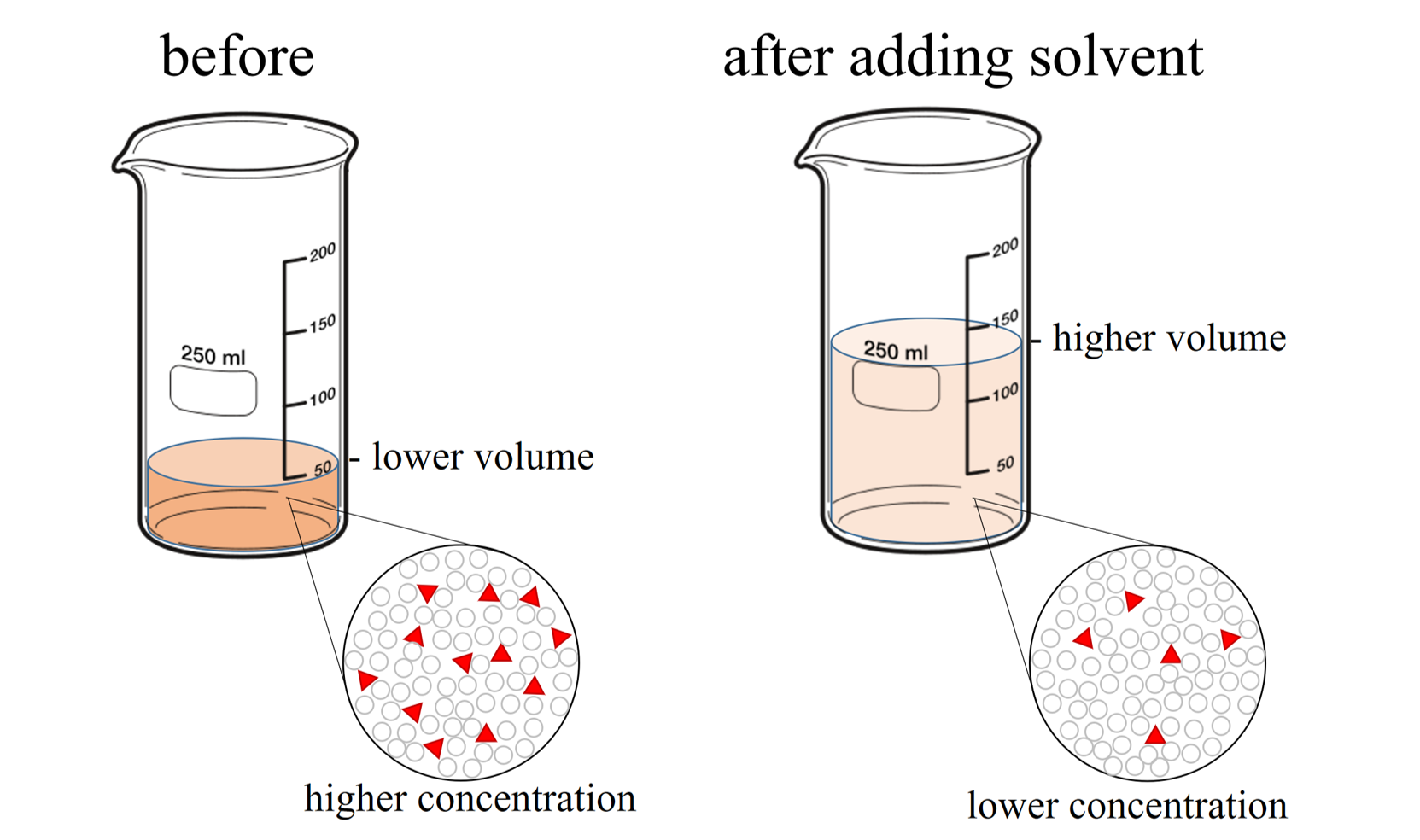
Once again, the amount of solute remains the same, so the moles of solute before dilution (1) are equal to the moles of solute after dilution (2):
\[\text{mol}_1 = \text{mol}_2\]
From the previous section, the moles of solute in a solution are equal to the molarity multiplied by the liters (mol = M × L), so:
\[M_1 \times L_1 = M_2 \times L_2\]
Since the two sides of the equation are equal, the volume (V) may be any unit we choose, as long as the units on each side are the same, meaning:
\[M_1 \times V_1 = M_2 \times V_2\]
Likewise, the concentration, (C) may be any unit we choose, as long as the concentration unit is based on the total volume of the solution and the unit on each side is the same. This yields the most general form of the dilution equation:
\[C_1V_1=C_2V_2\]
To summarize, C stands for the concentration of the solution, V for the volume of the solution, a subscript of 1 means before dilution, and a subscript of 2 means after dilution. Preparing dilutions is a common activity in the chemistry lab and elsewhere. Once you understand this relationship, the calculations are simple.
Suppose there are 100. mL of a 2.0 M solution of HCl available. The solution is diluted by adding enough water to make 500. mL of solution. The new molarity is easily calculated by rearranging the dilution equation and solving for C2.
\(\dfrac{C_1V_1}{V_2}=\dfrac{C_2\cancel{V_2}}{\cancel{V_2}}\;\;\;\Rightarrow\;\;C_2=\dfrac{C_1V_1}{V_2}=\dfrac{(2.0\;\mathrm M\;\mathrm{HCl})(100\;\cancel{\mathrm{mL}})}{500\;\cancel{\mathrm{mL}}}=0.40\;\mathrm M\;\mathrm{HCl}\)
It should make sense that if the original volume is ⅕ of the final volume, then the diluted solution should be ⅕ of its original concentration.
What is the concentration of a solution prepared by diluting 10.00 mL of a \(20.0\%\left({\textstyle\frac{\mathrm m}{\mathrm v}}\right)\;{\mathrm C}_6{\mathrm H}_{12}{\mathrm O}_6\) stock solution to a final volume of 200.0 mL?
Solution
| Steps for Problem Solving | |
|---|---|
| Identify the "given" information and what the problem is asking you to "find." | Given: C1 = \(20.0\%\left({\textstyle\frac{\mathrm m}{\mathrm v}}\right)\;{\mathrm C}_6{\mathrm H}_{12}{\mathrm O}_6\); V1 = 10.00 mL; V2 = 200.0 mL Find: C2 |
List known relationship(s). |
Dilution equation: \(C_1V_1=C_2V_2\) |
Rearrange the dilution equation and solve for C2. |
\(\dfrac{C_1V_1}{V_2}=\dfrac{C_2\cancel{V_2}}{\cancel{V_2}}\;\;\;\Rightarrow\;\;C_2=\dfrac{C_1V_1}{V_2}\) |
| Calculate the answer. | Plug the known quantities into the equation: \(C_2=\dfrac{C_1V_1}{V_2}=\dfrac{\left(20.0\%\left(\frac{\mathrm m}{\mathrm v}\right)\;{\mathrm C}_6{\mathrm H}_{12}{\mathrm O}_6\right)\left(10.00\;\cancel{\mathrm{mL}}\right)}{200.0\;\cancel{\mathrm{mL}}}=\boxed{1.00\%\left({\textstyle\frac{\mathrm m}{\mathrm v}}\right)\;{\mathrm C}_6{\mathrm H}_{12}{\mathrm O}_6}\) |
| Think about your result. | The volume before dilution is \(\frac1{20}\) the final volume, so it makes sense that the concentration after dilution is \(\frac1{20}\) its original concentration. |
Nitric acid, HNO3, is a powerful and corrosive acid. When ordered from a chemical supply company, its molarity is 16 M. How much of this stock solution, in mL, of nitric acid are needed to prepare 8.00 L of a 0.50 M solution?
Solution
| Steps for Problem Solving | |
|---|---|
| Identify the "given" information and what the problem is asking you to "find." | Given: C1 = 16 M HNO3; C2 = 0.50 M HNO3; V2 = \(8.00\;\cancel{\mathrm L}\;\times\dfrac{1000\;\mathrm{mL}}{1\cancel{\;\mathrm L}}=\;8000\;\mathrm{mL}\) (V2 converted to mL, since answer will be in mL. Volume units must be the same.) Find: V1 (in mL) |
List known relationship(s). |
Dilution equation: \(C_1V_1=C_2V_2\) |
Rearrange the dilution equation and solve for V1. |
\(\dfrac{\cancel{C_1}V_1}{\cancel{C_1}}=\dfrac{C_2V_2}{C_1}\;\;\;\Rightarrow\;\;V_1=\dfrac{C_2V_2}{C_1}\) |
| Calculate the answer. | Plug the known quantities into the equation: \(V_1=\dfrac{C_2V_2}{C_1}=\dfrac{\left(0.50\;\cancel{\mathrm M\;{\mathrm{HNO}}_3}\right)\left(8000\;\mathrm{mL}\right)}{16\;\cancel{\mathrm M\;{\mathrm{HNO}}_3}}=\boxed{250\;\mathrm{mL}}\) |
| Think about your result. | The final concentration is \(\frac1{32}\) its original concentration, so it makes sense that the volume of the stock solution used is \(\frac1{32}\) of the final volume. |
✏️ Exercise \(\PageIndex{1}\)
A 0.885 M solution of KBr with an initial volume of 76.5 mL has more water added until its concentration is 0.500 M. What is the new volume of the solution?
- Answer
-
135 mL
✏️ Exercise \(\PageIndex{2}\)
- What volume of a 6.0 ppb Hg2+ solution would be needed to prepare 600 mL of 0.10 ppb Hg2+ solution?
- Assuming the volumes are additive, describe how the diluted solution would be prepared.
- Answer A
- 10. mL of 6.0 ppb Hg2+ solution are needed.
- Answer B
- The solution would be prepared by thoroughly mixing 10 mL of the 6.0 ppb Hg2+ solution with 590 mL of water. This mixture makes 600 mL of solution.
This page is shared under a CK-12 license and was authored, remixed, and/or curated by Ed Vitz (Kutztown University), John W. Moore (UW-Madison), Justin Shorb (Hope College), Xavier Prat-Resina (University of Minnesota Rochester), Tim Wendorff, Adam Hahn, Melissa Alviar-Agnew, Henry Agnew, and Lance S. Lund (Anoka-Ramsey Community College). Original source: https://www.ck12.org/c/chemistry/.





