11.7: Predicting the Shapes of Molecules

⚙️ Learning Objective

• Determine the shape of simple molecules.

All molecules have a three-dimensional shape. There is an abundance of experimental evidence to that effect – from their physical properties to their chemical reactivity. Small molecules – molecules with a single central atom – have shapes that are easily predicted. The model used to predict molecular shapes is called the valence shell electron pair repulsion (VSEPR) model. The VSEPR model is based on the fact that electron pairs, being composed of negatively charged particles, repel each other to get as far away from one another as possible in three-dimensional space.

The VSEPR model makes a distinction between electron group geometry, which expresses how electron groups (bonds and nonbonding electron pairs) are arranged, and molecular geometry, which expresses how the atoms in a molecule are arranged. However, the two geometries are related.

There are two types of electron groups:

1. any type of bond – single, double, or triple.
2. lone electron pairs.

This text will not belabor how molecular geometries are determined. However, the VSPER model comes in handy when explaining why a water molecule is bent, while a carbon dioxide molecule is linear, even though they both have three atoms. When applying the VSEPR model to simple molecules, it all boils down to the number of electron groups around the central atom. Remember that a double or triple bond counts as only one electron group.

Linear molecules are simple. Any molecule with only two atoms is linear. A three-atom molecule whose central atom contains no lone pairs will orient the surrounding atoms as far apart from each other as possible in three-dimensional space – 180°, or linear, is as far apart apart as they can go. Carbon dioxide, CO₂, is such an example. The central carbon atom satisfies the octet rule by making two double bonds; it has no lone pairs. Therefore, the oxygen atoms lie on opposite sides of the molecule, or at 180° to each other around the carbon atom.

Figure \(\PageIndex{1}\) (left to right): The Lewis structure of CO₂. A three-dimensional rendering of CO₂.

Great! So, if water molecules have three atoms, just like carbon dioxide, then why are water molecules bent, while carbon dioxide molecules are linear? To understand this, it may be helpful to go back to the basics of the VSEPR model. Once again, the VSEPR model is based on the fact that electron pairs repel each other to get as far away from one another as possible in three-dimensional space. 

Water molecules are surrounded by four electron groups, just like molecules of methane, CH₄:

In the case of water, the four electron groups that surround the central oxygen atom includes two single bonds and two lone pairs of electrons. In the case of methane, the four electron groups that surround the central carbon atom includes four single bonds and zero lone pairs of electrons. In three-dimensional space, the farthest apart one can place the four surrounding hydrogen atoms is at 109.5° angles to the central carbon atom. If one drew imaginary lines from hydrogen atom to hydrogen atom in a methane molecule, the shape of a tetrahedron is obtained. Consequently, the geometry of four electron groups around a central atom is called a tetrahedral geometry.

Figure \(\PageIndex{2}\) (left to right): A three-dimensional rendering of CH₄, a tetrahedron, and the three-dimensional structure of CH₄ drawn inside a tetrahedron.

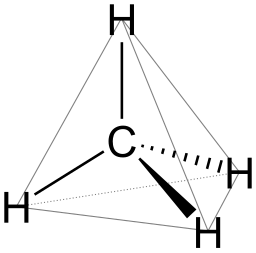The oxygen atom in a water molecule is still surrounded by four electron groups. It's just that two of those groups are lone pairs and those lone pairs still have repulsions and take up space in three-dimensions. However, when we look at the molecule, we "see" the atoms and not the electrons. As a result, what we see is a water molecule that has a bent shape, rather than linear.

Figure \(\PageIndex{3}\) (left to right): The Lewis structure of H₂O, including lone pairs, superimposed over its three-dimensional rendering. A three-dimensional rendering of H₂O.

For the large part, this text will provide three-dimensional renderings of molecules that have four or more atoms. It would be helpful to be able to predict whether three atom molecules are linear or bent. Because of the important role that water plays in the chemistry of so many things around us, you should definitely be aware that water is a bent molecule and not linear.
 

✅ Example \(\PageIndex{1}\)

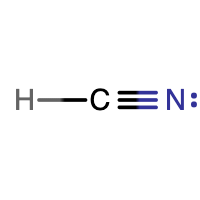
Draw the Lewis structure of HCN that reflects its correct three-dimensional geometry (bent or linear).

Solution

HCN is a linear molecule, since it has only two electron groups and there are no lone pairs on the central carbon atom.

 

✏️ Exercise \(\PageIndex{1}\)

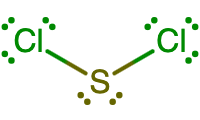
Draw the Lewis structure of SCl₂ that reflects its correct three-dimensional geometry (bent or linear).

Answer

SCl₂ is a bent molecule, since the central sulfur atom has two lone pairs in addition to the two covalent bonds it makes to the two chlorine atoms.
 

Summary

• The approximate shape of a molecule can be predicted from the number of electron groups and the number of surrounding atoms.

 

 

---

This page is shared under a CC BY-NC-SA 4.0 license and was authored, remixed, and/or curated by Lance S. Lund (Anoka-Ramsey Community College), Marisa Alviar-Agnew, and Henry Agnew.