8.6: Limiting Reactants and Excess Reactants
- Page ID
- 353404
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Learning Objectives
- Identify the limiting reactant (limiting reagent) in a given chemical reaction.
- Calculate how much product will be produced from the limiting reactant.
- Calculate how much reactant(s) remains when the reaction is complete.
Section 8.2 used an automobile factory to introduce terminology that extends to the stoichiometry associated with chemical reactions. We learned that the limiting reactant is the reactant that limits the amount of product that can be made, while an excess reactant is one that is not entirely consumed. We also learned that the theoretical yield is the maximum amount of product that may be made when all of the limiting reactant is converted to product.
Check out the simulation below for examples that review the concept of limiting reactants and excess reactants and applies the concept to making sandwiches and molecules. Then test your understanding with a game.
PhET Simulation: Limiting and Excess Reactants
View this interactive simulation illustrating the concepts of limiting and excess reactants.
Consider the reaction between hydrogen and chlorine to make hydrogen chloride:
The balanced equation shows that hydrogen and chlorine react in a 1:1 stoichiometric ratio. If these reactants are provided in any other amounts, one of the reactants will nearly always be entirely consumed, thus limiting the amount of product that may be generated. This substance is the limiting reactant, and the other substance is the excess reactant. Identifying the limiting and excess reactants for a given situation requires computing the molar amounts of each reactant provided and comparing them to the stoichiometric amounts represented in the balanced chemical equation.
For example, imagine combining 3 moles of H2 and 2 moles of Cl2. This represents a 3:2 (or 1.5:1) ratio of hydrogen to chlorine present for reaction, which is greater than the stoichiometric ratio of 1:1. Hydrogen, therefore, is present in excess, and chlorine is the limiting reactant. Reaction of all of the provided chlorine (2 moles) will consume 2 of the 3 moles of hydrogen provided, leaving 1 mole of hydrogen that is unconsumed (see Figure \(\PageIndex{1}\)).
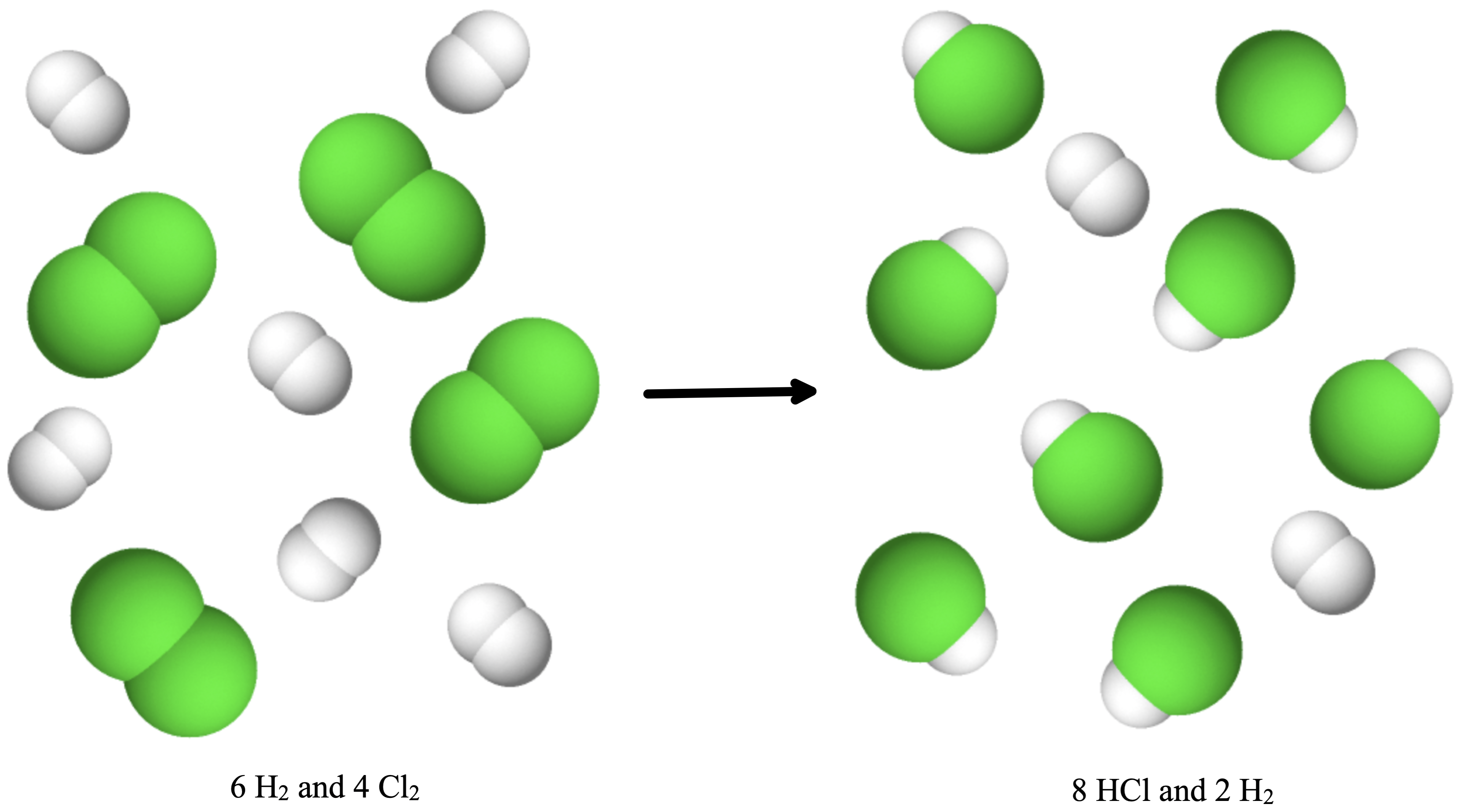
An alternative approach to identifying the limiting reactant involves comparing the amount of product expected for the complete reaction of each reactant. Each reactant amount is used to separately calculate the amount of product that would be formed per the reaction’s stoichiometry. The reactant yielding the lesser amount of product is the limiting reactant.
If we were to again imagine combining 3 moles of H2 and 2 moles of Cl2, complete reaction of the provided hydrogen would yield:
\(3\:\cancel{\mathrm{mol}\:{\mathrm H}_2}\times\dfrac{2\:\mathrm{mol}\:\mathrm{HCl}}{1\:\cancel{\mathrm{mol}\:{\mathrm H}_2}}=6\:\mathrm{mol}\:\mathrm{HCl}\;\mathrm{produced}\)
Complete reaction of the provided chlorine would produce:
\(2\:\cancel{\mathrm{mol}\:{\mathrm{Cl}}_2}\times\dfrac{2\:\mathrm{mol}\:\mathrm{HCl}}{1\:\cancel{\mathrm{mol}\:{\mathrm{Cl}}_2}}=\boxed{4\:\mathrm{mol}\:\mathrm{HCl}\;\mathrm{produced}}\)
The chlorine will be completely consumed once 4 moles HCl have been produced. Since enough hydrogen was provided to yield 6 moles HCl, there will be hydrogen that remains unconsumed once this reaction is complete.
A similar situation exists for many chemical reactions: you usually run out of one reactant before all of the other reactant has reacted. The reactant that is entirely consumed is called the limiting reactant; the other reactant or reactants are present in excess. A crucial skill in evaluating the conditions of a chemical process is to determine which reactant is the limiting reactant and which is/are the excess reactant(s).
The key to recognizing which reactant is the limiting reactant is to determine the reactant that yields the least amount of product is the limiting reactant. It doesn't matter which product is used for the calculation, as long as the same product is used in for the comparison. It also doesn't matter whether the number of moles or grams of that product is calculated. However, knowing the final mass of product is generally more useful.
✅ Example \(\PageIndex{1}\): Limiting Reactants and Mole-to-Mole Calculations
Consider the balanced equation:
4 C2H3Br3 + 11 O2 → 8 CO2 + 6 H2O + 6 Br2
- How many moles of Br2 could be produced when 36 mol C2H3Br3 are reacted with 33 mol O2?
- Identify the limiting reactant(s) and excess reactant(s).
Solution
| Steps for Problem Solving | |
|---|---|
| Identify the "given" information and what the problem is asking you to "find." | Given: 36 mol C2H3Br3 reacted; 33 mol O2 reacted Find: theoretical yield Br2; identify limiting reactant(s) and excess reactant(s) |
| List other known quantities. | 4 mol C2H3Br3: 6 mol Br2 11 mol O2: 6 mol Br2 |
| Prepare concept maps using the proper conversion factor(s). | \({\color[rgb]{0.8, 0.0, 0.0}\boxed{\mathrm{mol}\;{\mathrm C}_2{\mathrm H}_3{\mathrm{Br}}_3}}\xrightarrow[{4\;\mathrm{mol}\;{\mathrm C}_2{\mathrm H}_3{\mathrm{Br}}_3}]{6\;\mathrm{mol}\;{\mathrm{Br}}_2}{\color[rgb]{0.0, 0.0, 1.0}\boxed{\;\;\;\mathrm{mol}\;{\mathrm{Br}}_2\;\;\;}}\) \({\color[rgb]{0.8, 0.0, 0.0}\boxed{\;\;\;\mathrm{mol}\;{\mathrm O}_2\;\;\;}}\xrightarrow[{11\;\mathrm{mol}\;{\mathrm O}_2}]{6\;\mathrm{mol}\;{\mathrm{Br}}_2}{\color[rgb]{0.0, 0.0, 1.0}\boxed{\;\;\;\mathrm{mol}\;{\mathrm{Br}}_2\;\;\;}}\) |
| Calculate the theoretical yield. Select the smallest answer. |
\(36\:\cancel{\mathrm{mol}\;{\mathrm C}_2{\mathrm H}_3{\mathrm{Br}}_3}\times\dfrac{6\;\cancel{\mathrm{mol}\;{\mathrm{Br}}_2}}{4\:\cancel{\mathrm{mol}\;{\mathrm C}_2{\mathrm H}_3{\mathrm{Br}}_3}}=\xcancel{54\;\mathrm{mol}\;{\mathrm{Br}}_2}\) \(33\:\cancel{\mathrm{mol}\;{\mathrm O}_2}\times\dfrac{6\;\cancel{\mathrm{mol}\;{\mathrm{Br}}_2}}{11\:\cancel{\mathrm{mol}\;{\mathrm O}_2}}=\boxed{18\;\mathrm{mol}\;{\mathrm{Br}}_2}\) |
| Identify the limiting reactant(s) and excess reactant(s). | The limiting reactant is O2 since it would yield the least amount of product (18 mol Br2). The excess reactant is C2H3Br3 since its complete reaction would have yielded up to 54 mol Br2. |
Think about your result. |
It usually is not possible to determine the limiting reactant looking at the initial amounts, since the reactants have different coefficients. |
✅ Example \(\PageIndex{2}\): Limiting Reactants and Mass-to-Mass Calculations
Consider once again the balanced equation:
4 C2H3Br3 + 11 O2 → 8 CO2 + 6 H2O + 6 Br2
- What is the theoretical yield of CO2, in grams, when 76.4 grams of C2H3Br3 are reacted with 49.1 grams of O2?
- Identify the limiting reactant(s) and excess reactant(s).
Solution
| Steps for Problem Solving | |
|---|---|
| Identify the "given" information and what the problem is asking you to "find." | Given: 76.4 g C2H3Br3 reacted; 49.1 g O2 reacted Find: theoretical yield CO2; identify limiting reactant(s) and excess reactant(s) |
| List other known quantities. | 1 mol C2H3Br3 = 266.74 g C2H3Br3 1 mol O2 = 32.00 g O2 1 mol CO2 = 44.01 g CO2 4 mol C2H3Br3: 8 mol CO2 11 mol O2: 8 mol CO2 |
| Prepare concept maps using the proper conversion factor(s). | \({\color[rgb]{0.5, 0.0, 0.5}\boxed{\;\mathrm g\;{\mathrm C}_2{\mathrm H}_3{\mathrm{Br}}_3\;}}\xrightarrow[{266.74\;\mathrm g\;{\mathrm C}_2{\mathrm H}_3{\mathrm{Br}}_3}]{1\;\mathrm{mol}\;{\mathrm C}_2{\mathrm H}_3{\mathrm{Br}}_3}{\color[rgb]{0.8, 0.0, 0.0}\boxed{\mathrm{mol}\;{\mathrm C}_2{\mathrm H}_3{\mathrm{Br}}_3}}\xrightarrow[{4\;\mathrm{mol}\;{\mathrm C}_2{\mathrm H}_3{\mathrm{Br}}_3}]{8\;\mathrm{mol}\;{\mathrm{CO}}_2}{\color[rgb]{0.0, 0.0, 1.0}\boxed{\;\mathrm{mol}\;{\mathrm{CO}}_2\;}}\xrightarrow[{1\;\mathrm{mol}\;{\mathrm{CO}}_2}]{44.01\;\mathrm g\;{\mathrm{CO}}_2}{\color[rgb]{0.0, 0.5, 0.0}\boxed{\;\;\;\mathrm g\;{\mathrm{CO}}_2\;\;\;}}\) \({\color[rgb]{0.5, 0.0, 0.5}\boxed{\;\;\;\;\mathrm g\;{\mathrm O}_2\;\;\;\;}}\xrightarrow[{32.00\;\mathrm g\;{\mathrm O}_2}]{1\;\mathrm{mol}\;{\mathrm O}_2}{\color[rgb]{0.8, 0.0, 0.0}\boxed{\;\;\;\mathrm{mol}\;{\mathrm O}_2\;\;\;}}\xrightarrow[{11\;\mathrm{mol}\;{\mathrm O}_2}]{8\;\mathrm{mol}\;{\mathrm{CO}}_2}{\color[rgb]{0.0, 0.0, 1.0}\boxed{\;\;\mathrm{mol}\;{\mathrm{CO}}_2\;\;}}\xrightarrow[{1\;\mathrm{mol}\;{\mathrm{CO}}_2}]{44.01\;\mathrm g\;{\mathrm{CO}}_2}{\color[rgb]{0.0, 0.5, 0.0}\boxed{\;\;\;\;\mathrm g\;{\mathrm{CO}}_2\;\;\;\;}}\) |
| Calculate the theoretical yield. Select the smallest answer. |
\(76.4\:\cancel{\mathrm g\;{\mathrm C}_2{\mathrm H}_3{\mathrm{Br}}_3}\times\dfrac{1\;\cancel{\mathrm{mol}\;{\mathrm C}_2{\mathrm H}_3{\mathrm{Br}}_3}}{266.74\:\cancel{\mathrm g\;{\mathrm C}_2{\mathrm H}_3{\mathrm{Br}}_3}}\times\dfrac{8\;\cancel{\mathrm{mol}\;{\mathrm{CO}}_2}}{4\:\cancel{\mathrm{mol}\;{\mathrm C}_2{\mathrm H}_3{\mathrm{Br}}_3}}\times\dfrac{44.01\;\mathrm g\;{\mathrm{CO}}_2}{1\;\cancel{\mathrm{mol}\;{\mathrm{CO}}_2}}=\boxed{25.2\;\mathrm g\;{\mathrm{CO}}_2}\) \(49.1\:\cancel{\mathrm g\;{\mathrm O}_2}\times\dfrac{1\;\cancel{\mathrm{mol}\;{\mathrm O}_2}}{32.00\:\cancel{\mathrm g\;{\mathrm O}_2}}\times\dfrac{8\;\cancel{\mathrm{mol}\;{\mathrm{CO}}_2}}{11\:\cancel{\mathrm{mol}\;{\mathrm O}_2}}\times\dfrac{44.01\;\mathrm g\;{\mathrm{CO}}_2}{1\;\cancel{\mathrm{mol}\;{\mathrm{CO}}_2}}=\xcancel{49.1\;\mathrm g\;{\mathrm{CO}}_2}\) |
| Identify the limiting reactant(s) and excess reactant(s). | The limiting reactant is C2H3Br3 since it would yield the least amount of product (25.2 g CO2). The excess reactant is O2 since its complete reaction would have yielded up to 49.1 g CO2. |
Think about your result. |
It usually is not possible to determine the limiting reactant looking at the initial masses, since the reactants have different molar masses and different coefficients. |
✅ Example \(\PageIndex{3}\): Limiting Reactant and Mass of Excess Reactant
5.00 g Rb are combined with 3.44 g MgCl2 according to the chemical reaction:
2 Rb (s) + MgCl2 (s) → Mg (s) + 2 RbCl (s)
- What mass of Mg is formed?
- What mass of which reactant is left over?
Solution
| Steps for Problem Solving | |
|---|---|
| Identify the "given" information and what the problem is asking you to "find." | Given: 5.00 g Rb reacted; 3.44 g MgCl2 reacted Find: theoretical yield Mg; identify excess reactant and its mass |
| List other known quantities. | 1 mol Rb = 85.47 g Rb 1 mol MgCl2 = 95.21 g MgCl2 1 mol Mg = 24.31 g Mg 2 mol Rb: 1 mol Mg 1 mol MgCl2: 1 mol Mg |
| Prepare concept maps using the proper conversion factor(s). | \({\color[rgb]{0.5, 0.0, 0.5}\boxed{\;\;\;\mathrm g\;\mathrm{Rb}\;\;\;}}\xrightarrow[{85.47\;\mathrm g\;\mathrm{Rb}}]{1\;\mathrm{mol}\;\mathrm{Rb}}{\color[rgb]{0.8, 0.0, 0.0}\boxed{\;\;\mathrm{mol}\;\mathrm{Rb}\;\;}}\xrightarrow[{2\;\mathrm{mol}\;\mathrm{Rb}}]{1\;\mathrm{mol}\;\mathrm{Mg}}{\color[rgb]{0.0, 0.0, 1.0}\boxed{\;\;\mathrm{mol}\;\mathrm{Mg}\;\;}}\xrightarrow[{1\;\mathrm{mol}\;\mathrm{Mg}}]{24.31\;\mathrm g\;\mathrm{Mg}}{\color[rgb]{0.0, 0.5, 0.0}\boxed{\;\;\;\mathrm g\;\mathrm{Mg}\;\;\;}}\) \({\color[rgb]{0.5, 0.0, 0.5}\boxed{\;\mathrm g\;{\mathrm{MgCl}}_2\;}}\xrightarrow[{95.21\;\mathrm g\;{\mathrm{MgCl}}_2}]{1\;\mathrm{mol}\;{\mathrm{MgCl}}_2}{\color[rgb]{0.8, 0.0, 0.0}\boxed{\mathrm{mol}\;{\mathrm{MgCl}}_2}}\xrightarrow[{2\;\mathrm{mol}\;{\mathrm{MgCl}}_2}]{1\;\mathrm{mol}\;\mathrm{Mg}}{\color[rgb]{0.0, 0.0, 1.0}\boxed{\;\;\mathrm{mol}\;\mathrm{Mg}\;\;}}\xrightarrow[{1\;\mathrm{mol}\;\mathrm{Mg}}]{24.31\;\mathrm g\;\mathrm{Mg}}{\color[rgb]{0.0, 0.5, 0.0}\boxed{\;\;\;\mathrm g\;\mathrm{Mg}\;\;\;}}\) |
| Calculate the theoretical yield. Select the smallest answer. |
\(5.00\:\cancel{\mathrm g\;\mathrm{Rb}}\times\dfrac{1\;\cancel{\mathrm{mol}\;\mathrm{Rb}}}{85.47\:\cancel{\mathrm g\;\mathrm{Rb}}}\times\dfrac{1\;\cancel{\mathrm{mol}\;\mathrm{Mg}}}{2\:\cancel{\mathrm{mol}\;\mathrm{Rb}}}\times\dfrac{24.31\;\mathrm g\;\mathrm{Mg}}{1\;\cancel{\mathrm{mol}\;\mathrm{Mg}}}=\boxed{0.711\;\mathrm g\;\mathrm{Mg}}\) \(3.44\:\cancel{\mathrm g\;{\mathrm{MgCl}}_2}\times\dfrac{1\;\cancel{\mathrm{mol}\;{\mathrm{MgCl}}_2}}{95.21\:\cancel{\mathrm g\;{\mathrm{MgCl}}_2}}\times\dfrac{1\;\cancel{\mathrm{mol}\;\mathrm{Mg}}}{1\:\cancel{\mathrm{mol}\;{\mathrm{MgCl}}_2}}\times\dfrac{24.31\;\mathrm g\;\mathrm{Mg}}{1\;\cancel{\mathrm{mol}\;\mathrm{Mg}}}=\xcancel{0.878\;\mathrm g\;\mathrm{Mg}}\) |
| Identify the limiting reactant(s) and excess reactant(s). | The limiting reactant is Rb since it would yield the least amount of product (0.711 g Mg). The excess reactant is MgCl2 since its complete reaction would have yielded up to 0.878 g Mg. |
| Calculate the mass of excess reactant that reacts. | Start with 5.00 g Rb, since it is the limiting reactant and known to completely react. \(5.00\:\cancel{\mathrm g\;\mathrm{Rb}}\times\dfrac{1\;\cancel{\mathrm{mol}\;\mathrm{Rb}}}{85.47\:\cancel{\mathrm g\;\mathrm{Rb}}}\times\dfrac{1\;\cancel{\mathrm{mol}\;{\mathrm{MgCl}}_2}}{2\;\cancel{\mathrm{mol}\;\mathrm{Rb}}}\times\dfrac{95.21\;\mathrm g\;{\mathrm{MgCl}}_2}{1\;\cancel{\mathrm{mol}\;{\mathrm{MgCl}}_2}}=\boxed{2.78\;\mathrm g\;{\mathrm{MgCl}}_2\;\mathrm{reacted}}\) |
| Calculate the mass of excess reactant that remains and think about the result. | We started with 3.44 g MgCl2 and found that 2.78 g MgCl2 reacted. This makes sense, since MgCl2 is the excess reactant. Less should react than we started with. 3.44 g MgCl2 initially – 2.78 g MgCl2 reacted = 0.66 g MgCl2 remain |
Given the balanced chemical equation:
2 C8H18 + 25 O2 → 16 CO2 + 18 H2O
- If 24.5 moles of C8H18 are reacted with 245 moles of O2, how many moles of CO2 are produced assuming complete reaction?
- How many moles of which reactant remain unconsumed?
- Answer A
- 157 mol CO2 are produced.
- Answer B
- 4.9 mol C8H18 remain unconsumed.
✏️ Exercise \(\PageIndex{2}\)
Potassium superoxide, KO2, is used in rebreathing gas masks to generate oxygen according to the equation below.
4 KO2 (s) + 2 H2O (l) → 4 KOH (s) + 3 O2 (g)
- What is the theoretical yield of oxygen, in units of grams, when 108 g of KO2 reacts with 16.8 g of H2O?
- Which reactant is the limiting reactant?
- Which reactant is present in excess?
- Answer A
- 36.5 g O2 are produced.
- Answer B
- The limiting reactant is KO2.
- Answer C
- H2O is present in excess.
This page is shared under a CC BY-NC-SA 4.0 license and was authored, remixed, and/or curated by Sarick Shah, Lance S. Lund (Anoka-Ramsey Community College), Marisa Alviar-Agnew, and Henry Agnew.

