3.3.2: Rate Laws
- Page ID
- 4328
In practice, the easiest way to measure the speed of a reaction is to measure the concentration of either the reactants or the products over time.
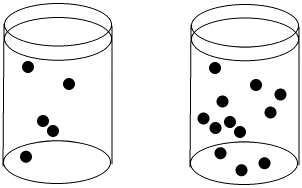
The concentration of black dots is higher in the beaker on the right than in the beaker on the left.
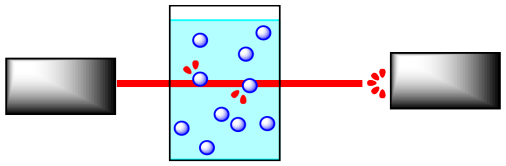
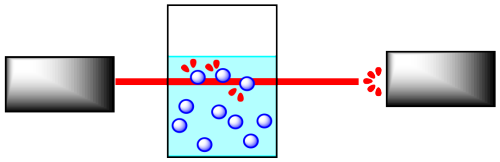
Reactions are often monitored by some form of spectroscopy. In spectroscopy, "light" or some other frequency of electromagnetic radiation passes through a reaction sample. The light interacts with the molecules in the sample, which absorb particular frequencies of light. Less light exits the sample than the amount that entered it; the amount that exits is measured by a detector on the other side.
If the concentration of the sample is different, a different amount of light from the spectrometer is absorbed. For instance, suppose the sample is more concentrated. The more molecules there are, the more light is absorbed. Because the beam of light travels through the sample in a straight line, the more concentrated the solution, the more molecules it encounters.
It is simple to calibrate the instrument to determine concentration from the amount of light absorbed. In addition, the light may interact with the reactant molecules and product molecules in different ways. This means that the absorption frequency of the reactants, and not the products, can be monitored, and thus changes in reactant concentration can be measured. This also works for the products..
The rate of reaction is written as:
\[\text{rate} = \frac{d[product]}{dt} \nonumber \]
In other words, the rate is equal to the change in concentration of product with change in time.
Concentration can be measured in several units. Frequently, the concentration of a solution is measured, and units such as grams per liter or, much more commonly, moles per liter, are used. The change in time is most often measured in seconds.
The rate of the reaction can also be written as follows:
\[\text{rate} = -\frac{d[reactant]}{dt} \nonumber \]
The rate is the change in concentration of reactant with change in time. The negative sign indicates that the reactant is being consumed over time as it turns into product, so its concentration is decreasing.
Kinetic studies are important in understanding reactions. Not only are they important in industry, but they are also used to understand biological processes, especially enzyme-catalyzed reactions. They also play a role in environmental and atmospheric chemistry, as part of an effort to understand a variety of issues ranging from the fate of prescription pharmaceuticals in wastewater to the cascade of reactions involved in the ozone cycle.
Contributors and Attributions
Chris P Schaller, Ph.D., (College of Saint Benedict / Saint John's University)