3.3.1: Order of Reaction Experiments
- Page ID
- 3817
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)This is an introduction to some of the experimental methods used in school laboratories to find orders of reaction. There are two fundamentally different approaches to this: investigating what happens to the initial rate of the reaction as concentrations change, and following a particular reaction to completion and processing the results from that single reaction.
Initial rate experiments
The simplest initial rate experiments involve measuring the time taken for some recognizable event to happen early in a reaction. This could be the time required for 5 cm3 of gas to be produced, for a small, measurable amount of precipitate to form, or for a dramatic color change to occur. Examples of these three indicators are discussed below.
The concentration of one of the components of the reaction could be changed, holding everything else constant: the concentrations of other reactants, the total volume of the solution and the temperature. The time required for the event to occur is then measured. This process is repeated for a range of concentrations of the substance of interest. A reasonably wide range of concentrations must be measured.This process could be repeated by altering a different property.
Understanding the results
Consider a simple example of an initial rate experiment in which a gas is produced. This might be a reaction between a metal and an acid, for example, or the catalytic decomposition of hydrogen peroxide. If volume of gas evolved is plotted against time, the first graph below results.
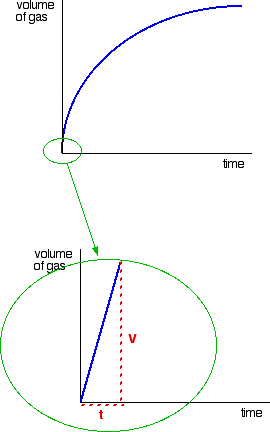
A measure of the rate of the reaction at any point is found by measuring the slope of the graph. The steeper the slope, the faster the rate. Because the initial rate is important, the slope at the beginning is used.
In the second graph, an enlarged image of the very beginning of the first curve, the curve is approximately straight. This is only a reasonable approximation when considering an early stage in the reaction. As the reaction progresses, the curvature of the graph increases. The slope of this linear region is V/t.
Suppose the experiment is repeated with a different (lower) concentration of the reagent. Again, the time it takes for the same volume of gas to evolve is measured, and the initial stage of the reaction is studied:
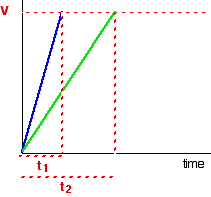
The initial rates (in terms of volume of gas produced per second) are given below:
| experiment 1 | |
| experiment 2 |
Now suppose V is unknown.
Suppose, for example, that instead of measuring the time taken to collect 5 cm3 of gas, the gas is collected up to a mark on the side of a test tube. If simply comparing initial rates, then it the distinction does not matter. As shown in the table above, the initial rate is inversely proportional to the time elapsed:
\[\text{initial rate} \propto \frac{1}{t} \nonumber \]
In experiments of this type, 1/t is often used as a measure of the initial rate.
The quantity 1/t can be plotted against the varying concentrations of the reactant of interest. If the reaction is first order with respect to that substance, then a straight line results; in a first order reaction, the rate is proportional to the concentration.
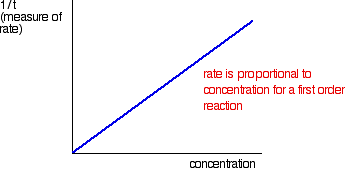
If a curve results, the reaction is not first order. It might be second order or a fractional order such as 1.5 or 1.78. The best way to deal with this is to plot what is known as a "log graph." In a reaction involving A, with an order of n with respect to A, the important part of the rate equation is the following:
\[ \text{rate} \propto [A]^n \nonumber \]
Taking the log of each side of the equation gives:
\[ \log (\text{rate}) \propto n\log [A] \nonumber \]
If log(rate) is plotted against log[A], a straight line with slope n is generated. The slope of the line is equal to the order of the reaction. Therefore, all rate values should be converted to log(rate). Then all the values for [A] are converted into log[A], and then the graph is plotted.
This is an example of measuring the initial rate of a reaction producing a gas.
![]()
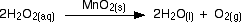
A simple set-up for this process is given below:
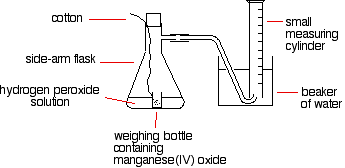
The reason for the weighing bottle containing the catalyst is to avoid introducing errors at the beginning of the experiment. The catalyst must be added to the hydrogen peroxide solution without changing the volume of gas collected. If it is added to the flask using a spatula before replacing the bung, some gas might leak out before the bung is replaced. Alternatively, air might be forced into the measuring cylinder. Either would render results meaningless.
To start the reaction, the flask is shaken until the weighing bottle falls over, and then shaken further to make sure the catalyst mixes evenly with the solution.
Alternatively, a special flask with a divided bottom could be used, with the catalyst in one side and the hydrogen peroxide solution in the other. The two are easily mixed by tipping the flask.
Using a 10 cm3 measuring cylinder, initially full of water, the time taken to collect a small fixed volume of gas can be accurately recorded. A small gas syringe could also be used.
To study the effect of the concentration of hydrogen peroxide on the rate, the concentration of hydrogen peroxide must be changed and everything else held constant —the temperature, the total volume of the solution, and the mass of manganese(IV) oxide. The manganese(IV) oxide must also always come from the same bottle so that its state of division is always the same.
The same apparatus can be used to determine the effects of varying the temperature, catalyst mass, or state of division due to the catalyst
Mixing dilute hydrochloric acid with sodium thiosulphate solution causes the slow formation of a pale yellow precipitate of sulfur.
\[ Na_2S_2O_{2(aq)} + 2HCl_{(aq)} \rightarrow 2NaCl_{(aq)} + H_2O_{(l)} + S_{(s)} + SO_{2(g)} \nonumber \]
A very simple, but very effective, way of measuring the time taken for a small fixed amount of precipitate to form is to stand the flask on a piece of paper with a cross drawn on it, and then look down through the solution until the cross disappears.
A known volume of sodium thiosulphate solution is placed in a flask. Then a small known volume of dilute hydrochloric acid is added, a timer is started, the flask is swirled to mix the reagents, and the flask is placed on the paper with the cross. The timer is used to determine the time for the cross to disappear. The process is repeated using a smaller volume of sodium thiosulphate, but topped up to the same original volume with water. Everything else is exactly as before.
The actual concentration of the sodium thiosulphate does not need to be known. In each case the relative concentration could be recorded. The solution with 40 cm3 of sodium thiosulphate solution plus 10 cm3 of water has a concentration which is 80% of the original, for example. The one with 10 cm3 of sodium thiosulphate solution plus 40 cm3 of water has a concentration 20% of the original.
The quantity 1/t can again be plotted as a measure of the rate, and the volume of sodium thiosulphate solution as a measure of concentration. Alternatively, relative concentrations could be plotted. In either case, the shape of the graph is the same.
The effect of temperature on this reaction can be measured by warming the sodium thiosulphate solution before adding the acid. The temperature must be measured after adding the acid, because the cold acid cools the solution slightly.This time, the temperature is changed between experiments, keeping everything else constant. To get reasonable times, a diluted version of the sodium thiosulphate solution must be used. Using the full strength, hot solution produces enough precipitate to hide the cross almost instantly.
There are several reactions bearing the name "iodine clock." Each produces iodine as one of the products. This is the simplest of them, because it involves the most familiar reagents.
The reaction below is the oxidation of iodide ions by hydrogen peroxide under acidic conditions:
\[ H_2O_{2(aq)} + 2I_{(aq)}^- + 2H^+ \rightarrow I_{2(aq)} + 2H_2O_{(l)} \nonumber \]
The iodine is formed first as a pale yellow solution, darkening to orange and then dark red before dark gray solid iodine is precipitated.
Iodine reacts with starch solution to give a deep blue solution. If starch solution is added to the reaction above, as soon as the first trace of iodine is formed, the solution turns blue. This gives no useful information. However, iodine also reacts with sodium thiosulphate solution:
\[ 2S_2O^{2-}_{3(aq)} + I_{2(aq)} \rightarrow S_2O_{6(aq)}^{2-} + 2I^-_{(aq)} \nonumber \]
If a very small amount of sodium thiosulphate solution is added to the reaction mixture (including the starch solution), it reacts with the iodine that is initially produced, so the iodine does not affect the starch, and there is no blue color. However, when that small amount of sodium thiosulphate is consumed, nothing inhibits further iodine produced from reacting with the starch. The mixture turns blue.
Following the course of a single reaction
Rather than performing a whole set of initial rate experiments, one can gather information about orders of reaction by following a particular reaction from start to finish. There are two different ways this can be accomplished.
- Samples of the mixture can be collected at intervals and titrated to determine how the concentration of one of the reagents is changing.
- A physical property of the reaction which changes as the reaction continues can be measured: for example, the volume of gas produced.
These approaches must be considered separately.
Sampling the reaction mixture
Bromoethane reacts with sodium hydroxide solution as follows:
\[ CH_3CH_2Br + OH^- \rightarrow CH_3CH_2OH + Br^- \nonumber \]
During the course of the reaction, both bromoethane and sodium hydroxide are consumed. However, it is relatively easy to measure the concentration of sodium hydroxide at any one time by performing a titration with a standard acid: for example, with hydrochloric acid of a known concentration.
The process starts with known concentrations of sodium hydroxide and bromoethane, and it is often convenient for them to be equal. Because the reaction is 1:1, if the concentrations are equal at the start, they remain equal throughout the reaction. Samples are taken with a pipette at regular intervals during the reaction, and titrated with standard hydrochloric acid in the presence of a suitable indicator. The problem with this approach is that the reaction is still proceeding in the time required for the titration. In addition, only one titration attempt is possible, because by the time another sample is taken, the concentrations have changed.
There are two ways around this problem:
- The reaction can be slowed by diluting it, adding the sample to a larger volume of cold water before the titration. Then the titration is performed as quickly as possible. This is most effective if the reaction is carried out above room temperature. Cooling it as well as diluting it slows it down even more.
- If possible (and it is possible in this case) it is better to stop the reaction completely before titrating. In this case, this can be accomplished by adding the sample to a known, excess volume of standard hydrochloric acid. This consumes all the sodium hydroxide in the mixture, stopping the reaction.
At this point the resulting solution is titrated with standard sodium hydroxide solution to determine how much hydrochloric acid is left over in the mixture. This allows one to calculate how much acid was used, and thus how much sodium hydroxide must have been present in the original reaction mixture. This technique is known as a back titration.
Processing the results
This process generates a set of values for concentration of (in this example) sodium hydroxide over time. The concentrations of bromoethane are, of course, the same as those obtained if the same concentrations of each reagent were used. These values are plotted to give a concentration-time graph, such as that below:
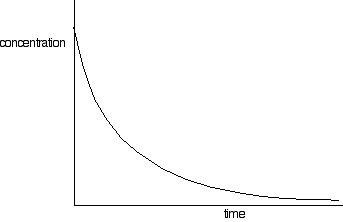
The rates of reaction at a number of points on the graph must be calculated; this is done by drawing tangents to the graph and measuring their slopes.
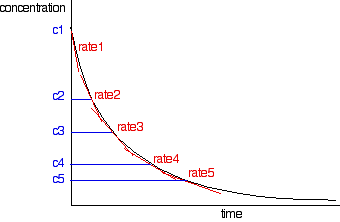
These values are then tabulated. The quickest way to proceed from here is to plot a log graph as described further up the page. All rates are converted to log(rate), and all the concentrations to log(concentration). Then, log(rate) is plotted against log(concentration). The slope of the graph is equal to the order of reaction.
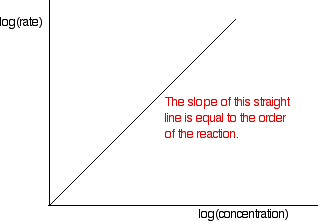
In the example of the reaction between bromoethane and sodium hydroxide solution, the order is calculated to be 2. Notice that this is the overall order of the reaction, not just the order with respect to the reagent whose concentration was measured. The rate of reaction decreases because the concentrations of both of the reactants decrease.
A familiar example is the catalytic decomposition of hydrogen peroxide (used above as an example of an initial rate experiment).
![]()
![]()
This time, measure the oxygen given off using a gas syringe, recording the volume of oxygen collected at regular intervals.
The practical side of this experiment is straightforward, but the calculation is not. The problem is that the volume of the product is measured, whereas the concentration of the reactants is used to find the reaction order. This means that the concentration of hydrogen peroxide remaining in the solution must be determined for each volume of oxygen recorded. This requires ideal gas law and stoichiometric calculations.
The table of concentrations and times is processed as described above.
Colorimetry
In any reaction involving a colored substance (either reacting or being produced), the reaction progress can be tracked using a colorimeter.

This entire setup can be contained in a small box. The color of the light can be controlled using a colored filter or diffraction grating. The color is chosen to be the frequency of light which is absorbed by the sample.
Taking copper(II) sulfate solution as a familiar example, a red filter is used because copper(II) sulfate solution absorbs red light. The more concentrated the solution is, the more of the red light it absorbs. A commonly quoted example of the use of colorimetry in reaction kinetics is the reaction between propanone and iodine in the presence of an acid catalyst:
\[ CH_3COCH_3 + I_2 \overset{H^+}{\longrightarrow} CH_3COCH_2I + H^+ + I^- \nonumber \]
The solution of iodine in propanone is initially brown, and then fades through orange to yellow to colorless as the iodine is consumed. A colorimeter measures the amount of light absorbed as it passes through a solution, recorded as the absorbance of the solution. It is common to plot a calibration curve for a colorimeter by making up solutions of the colored substance of known concentration and then measuring the absorbance of each under the same conditions. Absorbance is then plotted against concentration to create the calibration curve.
Two other methods
pH measurements: In a reaction in which hydrogen ions are reacting or being produced, changes in their concentration can in principle be tracked using a pH meter. The pH is a measure of hydrogen ion concentration, and an actual hydrogen ion concentration is easily calculated from a pH. However, when measuring pH over a fairly narrow range of hydrogen ion concentrations, the pH does not change much.
For example, a solution containing 0.2 mol dm-3 H+ has a pH of 0.70. By the time that the concentration has decreased to 0.1 mol dm-3, the pH has only increased to 1.00. The feasibility of using a pH meter depends on its accuracy; if the pH meter only records to 0.1 pH units, the results may not be adequate.
Conductivity measurements: The electrical conductivity of a liquid depends on the number of ions present, and the nature of the ions. For example, consider the following reaction:
![]()
![]()
During the course of the reaction, as hydrogen ions and iodide ions are consumed, the conductivity of the mixture decreases.


