Concluding Comments
- Page ID
- 71102
Concluding Comments – Peak broadening in Chromatographic Systems
Can you now draw a generalized plot of h versus flow rate?
We have now developed all four contributions to peak broadening in chromatographic systems, compared their significance in gas and liquid chromatography, and seen how current state-of-the-art columns have been designed to minimize band broadening effects. We can now pull together all four of the contributions into one equation that reflects overall contributions to peak broadening. It is shown below, using one common way of expressing the eddy diffusion term:
h = Av1/3 + B/v + CS v + CM v
It is worthwhile examining the overall form of this expression. First note how the longitudinal diffusion term (B/v) will become very large at very low flow rates. Note how the mass transport terms (CS v and CM v) will become very large at very high flow rates. This implies that this equation will have a minimum at some intermediate flow rate. A generalized plot of this equation for a gas chromatographic packed column is shown below. The general contributions of the longitudinal diffusion and mass transport terms to the equation are also represented. The optimal flow rate for a gas chromatographic packed column is around 15 to 20 mL/minute. A lot of times people actually run these at higher flow rates of about 30 mL/minute. The reason for this is to shorten the analysis time. Some column efficiency is sacrificed, but the entire separation process is a balance between chromatographic efficiency and analysis time, where there is a desirability to shorten this if possible.
A similar plot is also shown below for liquid chromatography. Notice in this case that extremely low flow rates must be used before longitudinal diffusion becomes a significant contribution to broadening. This means that the optimal flow rate for liquid chromatographic separations is very slow, which is undesirable because of the long analysis times this would create. Instead, a common flow rate for a packed C18 liquid chromatographic column is in the 1.0 to 1.5 mL/minute range.
For capillary GC columns, which are more commonly used today than packed GC columns, instead of setting a column flow rate you often set the column head pressure to a value recommended by the instrument manufacturer. By adjusting the pressure of the carrier gas (usually helium) at the beginning of the column, this insures an adequate flow of gas through the column. The desired head pressure depends on the length and internal diameter of the capillary column. Longer or narrower columns will require higher pressures to maintain adequate flow. One observation is that the pressure of the gas drops from the beginning to the end of the column, such that the flow rate changes over the column as well. Instead of measuring a flow rate for a fused silica capillary column in mL/min, it is more common to measure the carrier gas velocity (u) in cm/sec. Since this value changes as well over the column, an average value is obtained by dividing the column length in cm by the retention time in seconds of an unretained compound.
\[\mathrm{u\: (cm/sec) = \dfrac{column\: length\: (cm)}{RT\: of\: unretained\: peak\: (sec)}}\]
A plot of the plate height versus carrier gas velocity for a column that is 25 m long and has a 0.25 mm internal diameter is shown below. The characteristic observation of an optimum velocity as which to minimize peak broadening is observed.
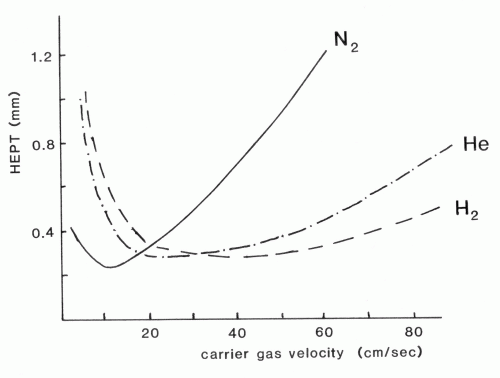
Why is the plot different for nitrogen versus helium as the carrier gas? The key difference between nitrogen and helium is the viscosity of the two gases. Nitrogen, as a heavier molecule, will have a higher viscosity than helium. The higher viscosity of nitrogen slows down the diffusion rates and increases the contribution of mobile phase mass transport broadening. Using helium as the carrier gas leads to improved efficiency because of the reduction in mobile phase mass transport broadening relative to nitrogen. Also, the uopt for helium is at a higher flow rate meaning that the analysis time can be shortened. This plot shows that hydrogen would actually be a better carrier gas than helium. Hydrogen is rarely used as a carrier gas because of its explosion risk.


