15.5: Marcus Theory for Electron Transfer
- Page ID
- 107311
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The displaced harmonic oscillator (DHO) formalism and the Energy Gap Hamiltonian have been used extensively in describing charge transport reactions, such as electron and proton transfer. Here we describe the rates of electron transfer between weakly coupled donor and acceptor states when the potential energy depends on a nuclear coordinate, i.e., nonadiabatic electron transfer. These results reflect the findings of Marcus’ theory of electron transfer.
We can represent the problem as calculating the transfer or reaction rate for the transfer of an electron from a donor to an acceptor
\[\ce{D + A \rightarrow D^{+} + A^{-}}\label{4.57}\]
This reaction is mediated by a nuclear coordinate \(q\). This need not be, and generally isn’t, a simple vibrational coordinate. For electron transfer in solution, we most commonly consider electron transfer to progress along a solvent rearrangement coordinate in which solvent reorganizes its configuration so that dipoles or charges help to stabilize the extra negative charge at the acceptor site. This type of collective coordinate is illustrated below.
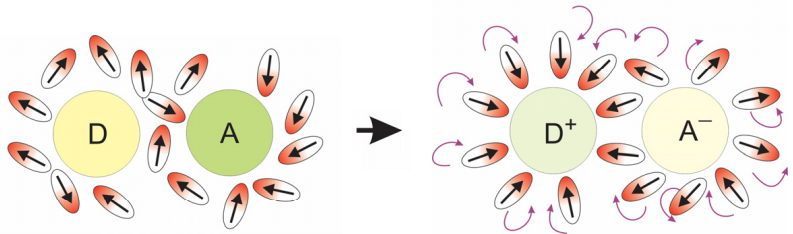
The external response of the medium along the electron transfer coordinate is referred to as “outer shell” electron transfer, whereas the influence of internal vibrational modes that promote ET is called “inner shell”. The influence of collective solvent rearrangements or intramolecular vibrations can be captured with the use of an electronic transition coupled to a harmonic bath.
Normally we associate the rates of electron transfer with the free-energy along the electron transfer coordinate \(q\). Pictures such as the ones above that illustrate states of the system with electron localized on the donor or acceptor electrons hopping from donor to acceptor are conceptually represented through diabatic energy surfaces. The electronic coupling \(J\) that results in transfer mixes these diabatic states in the crossing region. From this adiabatic surface, the rate of transfer for the forward reaction is related to the flux across the barrier. From classical transition state theory we can associate the rate with the free energy barrier using
\[k _ {f} = A \exp \left( - \Delta G^{\dagger} / k _ {B} T \right)\]
If the coupling is weak, we can describe the rates of transfer between donor and acceptor in the diabatic basis with perturbation theory. This accounts for nonadiabatic effects and tunneling through the barrier.
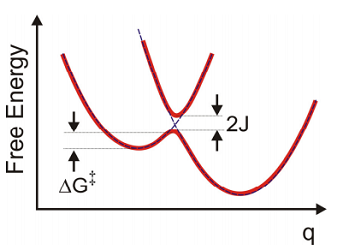
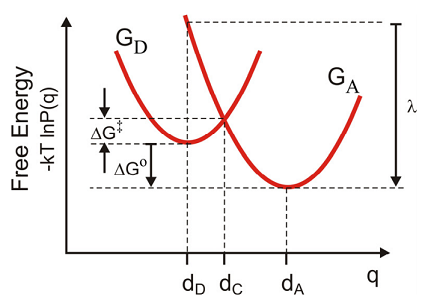
To begin we consider a simple classical derivation for the free-energy barrier and the rate of electron transfer from donor to acceptor states for the case of weakly coupled diabatic states. First we assume that the free energy or potential of mean force for the initial and final state,
\[\mathrm {G} ( \mathrm {q} ) = - \mathrm {k} _ {\mathrm {B}} \mathrm {T} \ln \mathrm {P} ( \mathrm {q} )\]
is well represented by two parabolas.
\[ \begin{align} G _ {D} ( q ) &= \frac {1} {2} m \omega _ {0}^{2} \left( q - d _ {D} \right)^{2} \label{14.58a} \\[4pt] G _ {A} ( q ) &= \frac {1} {2} m \omega _ {0}^{2} \left( q - d _ {A} \right)^{2} + \Delta G^{0} \label{14.58b} \end{align} \]
To find the barrier height \(\Delta G^{\dagger}\), we first find the crossing point \(dC\) where
\[G_D(d_C) = G_A(d_C). \label{14.58c}\]
Substituting Equations \ref{14.58a} and \ref{14.58b} into Equation \ref{14.58c}
\[ \frac {1} {2} m \omega _ {0}^{2} \left( d _ {c} - d _ {D} \right)^{2} = \Delta G^{\circ} + \frac {1} {2} m \omega _ {0}^{2} \left( d _ {C} - d _ {A} \right)^{2} \]
and solving for \(d_C\) gives
\[ \begin{align} d _ {C} &= \frac {\Delta G^{\circ}} {m \omega _ {0}^{2}} \left( \frac {1} {d _ {A} - d _ {D}} \right) + \frac {d _ {A} + d _ {D}} {2} \\[4pt] & = \frac {\Delta G^{\circ}} {2 \lambda} \left( d _ {A} - d _ {D} \right) + \frac {d _ {A} + d _ {D}} {2} \end{align} .\]
The last expression comes from the definition of the reorganization energy (\(\lambda\)), which is the energy to be dissipated on the acceptor surface if the electron is transferred at \(d_D\),
\[\begin{align} \lambda & = G _ {A} \left( d _ {D} \right) - G _ {A} \left( d _ {A} \right) \\ & = \frac {1} {2} m \omega _ {0}^{2} \left( d _ {D} - d _ {A} \right)^{2} \label{14.59} \end{align} \]
Then, the free energy barrier to the transfer \(\Delta G^{\dagger}\) is
\[\begin{aligned} \Delta G^{\dagger} & = G _ {D} \left( d _ {C} \right) - G _ {D} \left( d _ {D} \right) \\ & = \frac {1} {2} m \omega _ {0}^{2} \left( d _ {C} - d _ {D} \right)^{2} \\ & = \frac {1} {4 \lambda} \left[ \Delta G^{\circ} + \lambda \right]^{2} \end{aligned}.\]
So the Arrhenius rate constant is for electron transfer via activated barrier crossing is
\[k _ {E T} = A \exp \left[ \frac {- \left( \Delta G^{\circ} + \lambda \right)^{2}} {4 \lambda k T} \right] \label{14.60}\]
This curve qualitatively reproduced observations of a maximum electron transfer rate under the conditions \(- \Delta G^{\circ} = \lambda\), which occurs in the barrierless case when the acceptor parabola crosses the donor state energy minimum.
We expect that we can more accurately describe nonadiabatic electron transfer using the DHO or Energy Gap Hamiltonian, which will include the possibility of tunneling through the barrier when donor and acceptor wavefunctions overlap. We start by writing the transfer rates in terms of the potential energy as before. We recognize that when we calculate thermally averaged transfer rates that this is equivalent to describing the diabatic free energy surfaces. The Hamiltonian is
\[H = H _ {0} + V \label{14.61}\]
with
\[H _ {0} = | D \rangle H _ {D} \langle D | + | A \rangle H _ {A} \langle A | \label{14.62}\]
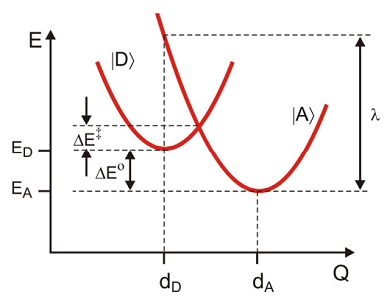
Here \(| D \rangle\) and \(| A \rangle\) refer to the potential where the electron is either on the donor or acceptor, respectively. Also remember that \(| D \rangle\) refers to the vibronic states
\[| D \rangle = | d , n \rangle.\]
These are represented through the same harmonic potential, displaced from one another vertically in energy by
\[\Delta E = E _ {A} - E _ {D}\]
and horizontally along the reaction coordinate \(q\):
\[\begin{align} H _ {D} &= | d \rangle E _ {D} \langle d | + H _ {d} \\[4pt] H _ {A} &= | a \rangle E _ {A} \langle a | + H _ {a} \label{14.63} \end{align} \]
\[\left.\begin{aligned} H _ {d} & = \hbar \omega _ {0} \left( p^{2} + \left( q - d _ {D} \right)^{2} \right) \\ H _ {a} & = \hbar \omega _ {0} \left( p^{2} + \left( q - d _ {A} \right)^{2} \right) \end{aligned} \right. \label{14.64}\]
Here we are using reduced variables for the momenta, coordinates, and displacements of the harmonic oscillator. The diabatic surfaces can be expressed as product states in the electronic and nuclear configurations: \(| D \rangle = | d , n \rangle\). The interaction between the surfaces is assigned a coupling \(J\)
\[V = J [ | d \rangle \langle a | + | a \rangle \langle d | ] \label{14.65}\]
We have made the Condon approximation, implying that the transfer matrix element that describes the electronic interaction has no dependence on nuclear coordinate. Typically this electronic coupling is expected to drop off exponentially with the separation between donor and acceptor orbitals;
\[J = J _ {0} \exp \left( - \beta _ {E} \left( R - R _ {0} \right) \right) \label{14.66}\]
Here \(\beta_E\) is the parameter governing the distance dependence of the overlap integral. For our purposes, even though this is a function of donor-acceptor separation (R), we take this to vary slowly over the displacements investigated here, and therefore be independent of the nuclear coordinate (\(Q\)).
Marcus evaluated the perturbation theory expression for the transfer rate by calculating Franck-Condon factors for the overlap of donor and acceptor surfaces, in a manner similar to our treatment of the DHO electronic absorption spectrum. Similarly, we can proceed to calculate the rates of electron transfer using the Golden Rule expression for the transfer of amplitude between two states
\[w _ {k \ell} = \frac {1} {\hbar^{2}} \int _ {- \infty}^{+ \infty} d t \left\langle V _ {I} (t) V _ {I} ( 0 ) \right\rangle \label{14.67}\]
Using
\[V _ {I} (t) = e^{i H _ {0} t / \hbar} V e^{- i H _ {0} t / \hbar},\]
we write the electron transfer rate in the DHO eigenstate form as
\[w _ {E T} = \frac {| J |^{2}} {\hbar^{2}} \int _ {- \infty}^{+ \infty} d t e^{- i \Delta E t / \hbar} F (t) \label{14.68}\]
where
\[F (t) = \left\langle e^{i H _ {d} t / h} e^{- i H _ {a} t / h} \right\rangle \label{14.69}\]
This form emphasizes that the electron transfer rate is governed by the overlap of vibrational wavepackets on the donor and acceptor potential energy surfaces.
Alternatively, we can cast this in the form of the Energy Gap Hamiltonian. This carries with is a dynamical picture of the electron transfer event. The energy of the two states have time-dependent (fluctuating) energies as a result of their interaction with the environment. Occasionally the energy of the donor and acceptor states coincide that is the energy gap between them is zero. At this point transfer becomes efficient. By integrating over the correlation function for these energy gap fluctuations, we characterize the statistics for barrier crossing, and therefore forward electron transfer.
Similar to before, we define a donor-acceptor energy gap Hamiltonian
\[H _ {A D} = H _ {A} - H _ {D} \label{14.70}\]
which allows us to write
\[F (t) = \left\langle \exp _ {+} \left[ - \frac {i} {\hbar} \int _ {0}^{t} d t^{\prime} H _ {A D} \left( t^{\prime} \right) \right] \right\rangle \label{14.71}\]
and
\[H _ {A D} (t) = e^{i H _ {d} t / \hbar} H _ {A D} e^{- i H _ {d} t / \hbar} \label{14.72}\]
These expressions and application of the cumulant expansion to equation allows us to express the transfer rate in terms of the lineshape function and correlation function
\[F (t) = \exp \left[ \frac {- i} {\hbar} \left\langle H _ {A D} \right\rangle t - g (t) \right] \label{14.73}\]
\[g (t) = \int _ {0}^{t} d \tau _ {2} \int _ {0}^{\tau _ {2}} d \tau _ {1} C _ {A D} \left( \tau _ {2} - \tau _ {1} \right) \label{14.74}\]
\[C _ {A D} (t) = \frac {1} {\hbar^{2}} \left\langle \delta H _ {A D} (t) \delta H _ {A D} ( 0 ) \right\rangle \label{14.75}\]
\[\left\langle H _ {A D} \right\rangle = \lambda \label{14.76}\]
The lineshape function can also be written as a sum of many coupled nuclear coordinates, \(q_{\alpha}\). This expression is commonly applied to the vibronic (inner shell) contributions to the transfer rate:
\[\begin{align} g (t) &= - \sum _ {\alpha} \left( d _ {\alpha}^{A} - d _ {\alpha}^{D} \right)^{2} \left[ \left( \overline {n} _ {\alpha} + 1 \right) \left( e^{- i \omega _ {\alpha} t} - 1 + i \omega _ {0} t \right) + \overline {n} _ {\alpha} \left( e^{i \omega _ {a} t} - 1 - i \omega _ {0} t \right) \right] \\[4pt] &= - \sum _ {\alpha} \left( d _ {\alpha}^{A} - d _ {\alpha}^{D} \right)^{2} \left[ \operatorname {coth} \left( \beta \hbar \omega _ {\alpha} / 2 \right) \left( \cos \omega _ {\alpha} t - 1 \right) - i \left( \sin \omega _ {\alpha} t - \omega _ {\alpha} t \right) \right] \label{14.77} \end{align}\]
Substituting the expression for a single harmonic mode into the Golden Rule rate expression gives
\[\begin{align} w _ {E T} &= \frac {| J |^{2}} {\hbar^{2}} \int _ {- \infty}^{+ \infty} d t e^{- i \Delta E t / \hbar - g (t)} \label{4.78} \\[4pt] &= \frac {| J |^{2}} {\hbar^{2}} \int _ {- \infty}^{+ \infty} d t e^{- i ( \Delta E + \lambda ) t / \hbar} \exp \left[ D \left( \operatorname {coth} \left( \beta \hbar \omega _ {0} / 2 \right) \left( \cos \omega _ {0} t - 1 \right) - i \sin \omega _ {0} t \right) \right] \label{14.78} \end{align}\]
where
\[D = \left( d _ {A} - d _ {D} \right)^{2} \label{14.79}\]
This expression is very similar to the one that we evaluated for the absorption lineshape of the Displaced Harmonic Oscillator model. A detailed evaluation of this vibronically mediated transfer rate is given in Jortner.
To get a feeling for the dependence of \(k\) on \(q\), we can look at the classical limit \(\hbar \omega \ll k T\). This corresponds to the case where one is describing the case of a low frequency “solvent mode” or “outer sphere” effect on the electron transfer. Now, we neglect the imaginary part of \(g(t)\) and take the limit
\[\operatorname {coth} ( \beta \hbar \omega / 2 ) \rightarrow 2 / \beta \hbar \omega\]
so
\[w _ {E T} = \frac {| J |^{2}} {\hbar^{2}} \int _ {- \infty}^{+ \infty} d t e^{- i ( \Delta E + \lambda ) t} \exp \left( - \left( \frac {2 D k _ {B} T} {\hbar \omega _ {0}} \right) \left( 1 - \cos \omega _ {0} t \right) \right) \label{14.80}\]
Note that the high temperature limit also means the low frequency limit for \(\omega _ {0}\). This means that we can expand
\[\cos \omega _ {0} t \approx 1 - \left( \omega _ {0} t \right)^{2} / 2,\]
and find
\[w _ {E T} = \frac {| J |^{2}} {\hbar} \sqrt {\frac {\pi} {\lambda k T}} \exp \left[ \frac {- ( \Delta E + \lambda )^{2}} {4 \lambda k T} \right] \label{14.81}\]
where \(\lambda = D \hbar \omega _ {0}\). Note that the activation barrier \(\Delta E^{\dagger}\) for displaced harmonic oscillators is \(\Delta E^{\dagger} = \Delta E + \lambda\). For a thermally averaged rate it is proper to associate the average energy gap with the standard free energy of reaction,
\[\left\langle H _ {A} - H _ {D} \right\rangle - \lambda = \Delta G^{0}.\]
Therefore, this expression is equivalent to the classical Marcus’ result for the electron transfer rate
\[k _ {E T} = A \exp \left[ \frac {- \left( \Delta G^{o} + \lambda \right)^{2}} {4 \lambda k T} \right] \label{14.82}\]
where the pre-exponential is
\[A = 2 \pi | J |^{2} / \hbar \sqrt {4 \pi \lambda k T} \label{14.83}\]
This expression shows the nonlinear behavior expected for the dependence of the electron transfer rate on the driving force for the forward transfer, i.e., the reaction free energy. This is unusual because we generally think in terms of a linear free energy relationship between the rate of a reaction and the equilibrium constant:
\[\ln k \propto \ln K _ {e q}.\]
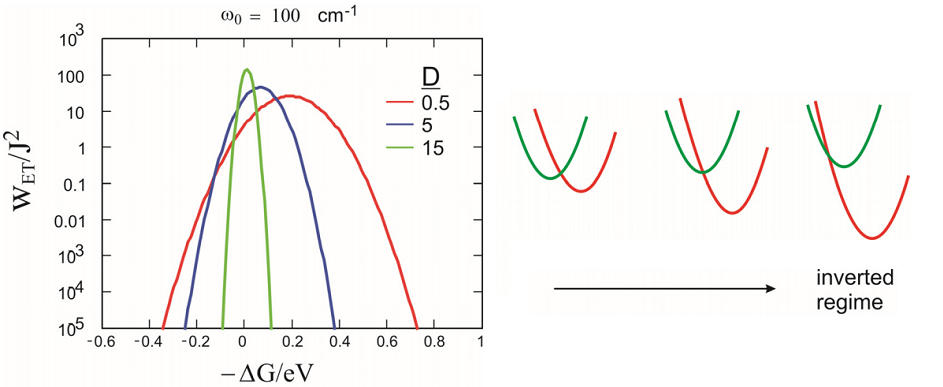
This leads to the thinking that the rate should increase as we increase the driving free energy for the reaction \(-\Delta G^{0}\). This behavior only hold for a small region in \(\Delta G^{0}\). Instead, eq. shows that the ET rate will increase with \(-\Delta G^{0}\), until a maximum rate is observed for \(-\Delta G^{0}=\lambda\) and the rate then decreases. This decrease of k with increased \(-\Delta G^{0}\) is known as the “inverted regime”. The inverted behavior means that extra vibrational excitation is needed to reach the curve crossing as the acceptor well is lowered. The high temperature behavior for coupling to a low frequency mode \(\left(100 \mathrm{~cm}^{-1} \text {at } 300 \mathrm{~K}\right)\) is shown at right, in addition to a cartoon that indicates the shift of the curve crossing at \(\Delta G^{0}\) in increased.
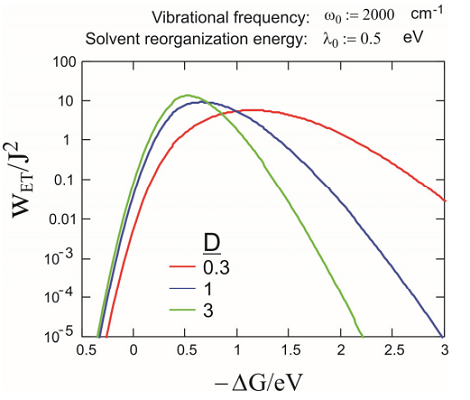
Particularly in intramolecular ET, it is common that one wants to separately account for the influence of a high frequency intramolecular vibration (inner sphere ET) that is not in the classical limit that applies to the low frequency classical solvent response. If an additional mode of frequency \(\omega _ {0}\) and a rate in the form of Equation \ref{14.81} is added to the low frequency mode, Jortner has given an expression for the rate as:
\[w _ {E T} = \frac {| J |^{2}} {\hbar} \sqrt {\frac {\pi} {\lambda _ {0} k T}} \sum _ {j = 0}^{\infty} \left( \frac {e^{- D}} {j !} D^{j} \right) \exp \left[ \frac {- \left( \Delta G^{o} + \lambda _ {0} + j \hbar \omega _ {0} \right)^{2}} {4 \lambda _ {0} k T} \right] \label{14.84}\]
Here \(\lambda _ {0}\) is the solvation reorganization energy. For this case, the same inverted regime exists; although the simple Gaussian dependence of \(k\) on \(\Delta G^{0}\) no longer exists. The asymmetry here exists because tunneling sees a narrower barrier in the inverted regime than in the normal regime. Examples of the rates obtained with eq. are plotted in the figure below (T= 300 K).
As with electronic spectroscopy, a more general and effective way of accounting for the nuclear motions that mediate the electron transfer process is to describe the coupling weighted density of states as a spectral density. Then we can use coupling to a harmonic bath to describe solvent and/or vibrational contributions of arbitrary form to the transfer event using
\[g (t) = \int _ {0}^{\infty} d \omega\, \rho ( \omega ) \left[ \operatorname {coth} \left( \frac {\beta \hbar \omega} {2} \right) ( 1 - \cos \omega t ) + i ( \sin \omega t - \omega t ) \right] \label{14.85}\]
Readings
- Barbara, P. F.; Meyer, T. J.; Ratner, M. A., Contemporary issues in electron transfer research. J. Phys. Chem. 1996, 100, 13148-13168, and references within.
- Georgievskii, Y.; Hsu, C.-P.; Marcus, R. A., Linear response in theory of electron transfer reactions as an alternative to the molecular harmonic oscillator model. The Journal of Chemical Physics 1999, 110, 5307-5317.
- Jortner, J., The temperature dependent activation energy for electron transfer between biological molecules. Journal of Chemical Physics 1976, 64, 4860-4867.
- Marcus, R. A.; Sutin, N., Electron transfers in chemistry and biology. Biochimica et Biophysica Acta (BBA) - Reviews on Bioenergetics 1985, 811, 265-322.
- Nitzan, A., Chemical Dynamics in Condensed Phases. Oxford University Press: New York, 2006; Ch. 10


