14.2: Line-Broadening and Spectral Diffusion
- Page ID
- 107301
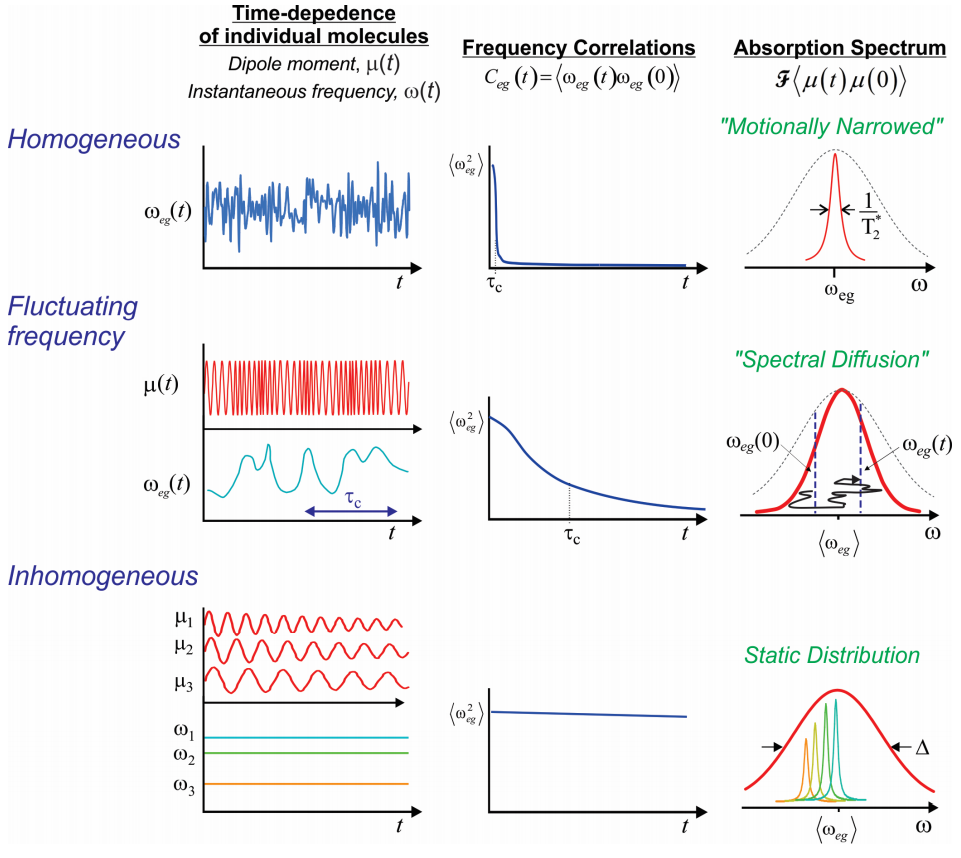
We will investigate how a fluctuating environment influences measurements of an experimentally observed internal variable. Specifically we focus on the spectroscopy of a chromophore, and how the chromophore’s interactions with its environment influence its transition frequency and absorption lineshape. In the absence of interactions, the resonance frequency that we observe is \(\omega_{eg}\). However, we have seen that interactions of this chromophore with its environment can shift this frequency. In condensed matter, time-dependent interactions with the surroundings can lead to time-dependent frequency shifts, known as spectral diffusion. How these dynamics influence the line width and lineshape of absorption features depends on the distribution of frequencies available to your system (\(\Delta\)) and the time scale of sampling varying environments (\(\tau_c\)). Consider the following cases of line broadening:
- Homogeneous. Here, the absorption lineshape is dynamically broadened by rapid variations in the frequency or phase of dipoles. Rapid sampling of a distribution of frequencies acts to average the experimentally observed resonance frequency. The result in a “motionally narrowed” line width that is narrower than the distribution of frequencies available and proportional to the rate of fluctuation induced dephasing.
- Inhomogeneous. In this limit, the lineshape reflects a static distribution of resonance frequencies, and the width of the line represents the distribution of frequencies, ', which arise, from different structural environments available to the system.
- Spectral Diffusion. More generally, every system lies between these limits. Given a distribution of configurations that the system can adopt, for instance an electronic chromophore in a liquid, an equilibrium system will be ergodic, and over a long enough time any molecule will sample all configurations available to it. Under these circumstances, we expect that every molecule will have a different “instantaneous frequency” \(\omega_i(t)\) which evolves in time as a result of its interactions with a dynamically evolving system. This process is known as spectral diffusion. The homogeneous and inhomogeneous limits can be described as limiting forms for the fluctuations of a frequency \(\omega_i(t)\) through a distribution of frequencies \(\Delta\). If \(\omega_i(t)\) evolves rapidly relative to \(\Delta^{-1}\), the system is homogeneously broadened. If \(\omega_i(t)\) evolves slowly the system is inhomogeneous broadened. This behavior can be quantified through the transition frequency time-correlation function \[C _ {e g} (t) = \left\langle \omega _ {e g} (t) \omega _ {e g} ( 0 ) \right\rangle \label{13.8}\] Our job will be to relate the transition frequency correlation function \(C _ {e g} (t)\) with the dipole correlation function that determines the lineshape, \(C _ {\mu \mu} (t)\).