9.1: Concepts and Definitions
- Page ID
- 107265
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)As one change to our thinking, we now have to be concerned with ensembles. Most often, we will be concerned with systems in an equilibrium state with a fixed temperature for which many quantum states are accessible to the system. For comparing calculations of pure quantum states to experimental observables on macroscopic samples, we assume that all molecules have been prepared and observed in the same manner, so that the quantum expectation values for the internal operators can be compared directly to experimental observations. For mixed states, we have seen the need to perform an additional layer of averaging over the ensemble in the calculation of expectation values.
Perhaps the most significant change between isolated states and condensed matter is the dynamics. From the time-dependent Schrödinger equation, we see that the laws governing the time evolution of isolated quantum mechanical systems are invariant under time reversal. That is, there is no intrinsic directionality to time. If one reverses the sign of time and thereby momenta of objects, we should be able to exactly reverse the motion and propagate the system to where it was at an earlier time. This is also the case for classical systems evolving under Newton’s equation of motion. In contrast, when a quantum system is in contact with another system having many degrees of freedom, a definite direction emerges for time, “the arrow of time,” and the system’s dynamics is no longer reversible. In such irreversible systems a welldefined prepared state decays in time to an equilibrium state where energy has been dissipated and phase relationships are lost between the various degrees of freedom.
Additionally, condensed phase systems on a local, microscopic scale all have a degree of randomness or noisiness to their dynamics that represent local fluctuations in energy on the scale of \(k _ {B} T\). This behavior is observed even through the equations of motion that govern the dynamics are deterministic. Why? It is because we generally have imperfect knowledge about all of the degrees of freedom influencing the system, or experimentally view its behavior through a highly restricted perspective. For instance, it is common in experiments to observe the behavior of condensed phases through a molecular probe imbedded within or under the influence of its surroundings. The physical properties of the probe are intertwined with the dynamics of the surrounding medium, and to us this appears as random behavior, for instance as Brownian motion. Other examples of the appearance of randomness from deterministic equations of motion include weather patterns, financial markets, and biological evolution. So, how do irreversible behavior and random fluctuations, hallmarks of all chemical systems, arise from the deterministic time-dependent Schrödinger equation? This fascinating question will be the central theme in our efforts going forward.
Definitions
Let’s begin by establishing some definitions and language that will be useful for us. We first classify chemical systems of interest as equilibrium or non-equilibrium systems. An equilibrium system is one in which the macroscopic properties (i.e., the intensive variables) are invariant with time, or at least invariant on the time scales over which one executes experiments and observes the system. Further, there are no steady state concentration or energy gradients (currents) in the system. Although they are macroscopically invariant, equilibrium states are microscopically dynamic.
For systems at thermal equilibrium we will describe their time-dependent behavior as dynamically reversible or irreversible. For us, reversible will mean that a system evolves deterministically. Knowledge of the state of the system at one point in time and the equation of motion means that you can describe the state of the system for all points in time later or previously. Irreversible systems are not deterministic. That is, knowledge of the state of the system at one point in time does not provide enough information to precisely determine its past state.
Since all states are irreversible in the strictest sense, the distinction is often related to the time scale of observation. For a given system, on a short enough time scale dynamics will appear deterministic whereas on very long times appear random. For instance, the dynamics of a dilute gas appear ballistic on time scales short compared to the mean collision time between particles, whereas their motion appears random and diffusive on much longer time scales. Memory refers to the ability to maintain deterministic motion and reversibility, and we will quantify the decay of memory in the system with correlation functions. For the case of quantum dynamics, we are particularly interested in the phase relationships between quantum degrees of freedom that results from deterministic motion under the time-dependent Schrödinger equation.
Nonequilibrium states refers to open or closed systems that have been acted on externally, moving them from equilibrium by changing the population or energy of the quantum states available to the system. Thermodynamically, work is performed on the system, leading to a free-energy gradient that the nonequilibrium system will minimize as it re-equilibrates. For nonequilibrium states, we will be interested in relaxation processes, which refer to the timedependent processes involved in re-equilibrating the system. Dissipation refers to the relaxation processes involving redistribution of energy as a nonequilibrium state returns toward a thermal distribution. However, there are other relaxation processes such as the randomization of the orientation of an aligned system or the randomization of phase of synchronized oscillations.
Statistics
With the need to describe ensembles, will use statistical descriptions of the properties and behavior of a system. The variable \(A\), which can be a classical internal variable or quantum operator, can be described statistically in terms of the mean and mean-square values of \(A\) determined from a large number of measurements:
\[\langle A \rangle = \frac {1} {N} \sum _ {i = 1}^{N} A _ {i} \label{8.1}\]
\[\left\langle A^{2} \right\rangle = \frac {1} {N} \sum _ {i = 1}^{N} A _ {i}^{2} \label{8.2}\]
Here, the summation over \(i\) refers to averaging over \(N\) independent measurements. Alternatively, these equations can be expressed as
\[\langle A \rangle = \sum _ {n = 1}^{M} P _ {n} A _ {n} \label{8.3}\]
\[\left\langle A^{2} \right\rangle = \sum _ {n = 1}^{M} P _ {n} A _ {n}^{2} \label{8.4}\]
The sum over \(n\) refers to a sum over the \(M\) possible values that \(A\) can take, weighted by \(P_n\), the probability of observing a particular value \(A_n\). When the accessible values come from a continuous as opposed to discrete distribution, one can describe the statistics in terms of the moments of the distribution function, \(P(A)\), which characterizes the probability of observing \(A\) between \(A\) and \(A+dA\)
\[\langle A \rangle = \int d A A P ( A ) \label{8.5}\]
\[\left\langle A^{2} \right\rangle = \int d A A^{2} P ( A ) \label{8.6}\]
For time-dependent processes, we recognize that it is possible that these probability distributions carry a time dependence, \(P(A,t)\). The ability to specify a value for \(A\) is captured in the variance of the distribution
\[\sigma^{2} = \left\langle A^{2} \right\rangle - \langle A \rangle^{2} \label{8.7}\]
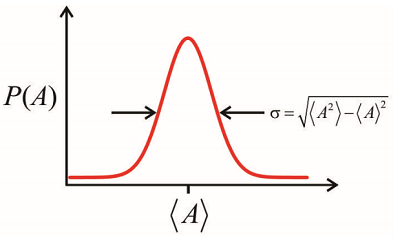
We will apply averages over probability distributions to the description of ensembles of molecules; however, we should emphasize that a statistical description of a quantum system also applies to a pure state. A fundamental postulate is that the expectation value of an operator
\[\langle \hat {A} \rangle = \langle \psi | \hat {A} | \psi \rangle\]
is the mean value of \(A\) obtained over many observations on identically prepared systems. The mean and variance of this expectation value represent the fundamental quantum uncertainty in a measurement.
To take this a step further and characterize the statistical relationship between two variables, one can define a joint probability distribution, \(P(A,B)\), which characterizes the probability of observing \(A\) between \(A\) and \(A+dA\) and \(B\) between \(B\) and \(B+dB\). The statistical relationship between the variables can also emerges from moments of \(P(A,B)\). The most important measure is a correlation function
\[C _ {A B} = \langle A B \rangle - \langle A \rangle \langle B \rangle \label{8.8}\]
You can see that this is the covariance—the variance for a bivariate distribution. This is a measure of the correlation between the variables \(A\) and \(B\). That is, for a specific value of \(A\), what are the associated statistics for \(B\). To interpret this it helps to define a correlation coefficient
\[r = \frac {C _ {A B}} {\sigma _ {A} \sigma _ {B}} \label{8.9}\]
\(r\) can take on values from +1 to -1. If \(r = 1\) then there is perfect correlation between the two distributions. If the variables \(A\) and \(B\) depend the same way on a common internal variable, then they are correlated. If no statistical relationship exists between the two distributions, then they are uncorrelated, \(r = 0\), and \(\langle A B \rangle = \langle A \rangle \langle B \rangle\). It is also possible that the distributions depend in an equal and opposite manner on an internal variable, in which case we call them anti-correlated with \(r = -1\).


