16.4: Henry's Law and the Fugacity and Activity of A Solution Component
- Page ID
- 151763
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)In describing the activities of solution components, we have taken the standard state of component \(A\) to be the pure liquid at its equilibrium vapor pressure, \(P^{\textrm{⦁}}_A\), at the temperature of the solution. We can also express the activity using Henry’s law. Henry’s law states that the partial pressure of a component above its solution is directly proportional to the concentration of the component. We can choose any convenient unit to express the solute concentration. The value of the proportionality constant depends on this choice. Using mole fraction as the unit of concentration, Henry’s law is
\[P_A=x_AP={\kappa }_Ay_A \nonumber \]
(Henry’s law)
where the proportionality constant, \({\kappa }_A\), is called the Henry’s-law constant. (When we write \(P_A=x_AP\), we implicitly assume that the gas-phase components of the equilibrium system behave as ideal gases.) Henry’s law is more general than Raoult’s law. Indeed, Raoult’s law is a special case of Henry’s law; if the solute obeys Raoult’s law, the Henry’s-law constant is \(P^{\textrm{⦁}}_A\).
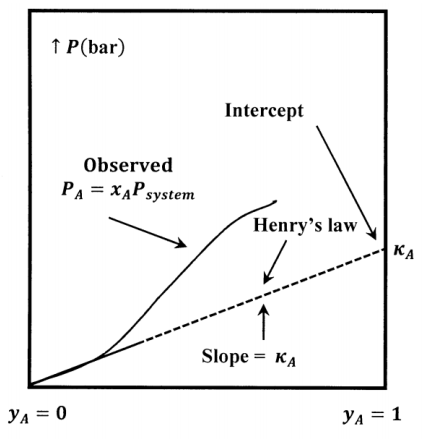
The value of the Henry’s-law constant depends on the components and the temperature. Experimentally, the value of the constant is determined by finding the slope of a plot of \(P_A\) versus \(y_A\) in the limit as \(y_A\to 0\). The sketch in Figure 5 illustrates the relationship between the \(P_A\) curve and the Henry’s-law tangent to it at \(y_A=0\). Note that the slope of the tangent line at \(y_A=0\) is equal to its intercept at \(y_A=1\).
In practice, a sufficiently low concentration of any non-electrolyte component, in any liquid solution, obeys Henry’s law. For this reason, we refer to the component that obeys Henry’s law as the solute. We designate the higher concentration component as the solvent. The universal validity of Henry’s law as a low-concentration approximation has a simple physical interpretation. The solute vapor pressure depends upon the net effects of solute–solute, solute–solvent, and solvent–solvent intermolecular forces.
If all of these intermolecular forces are the same, the intermolecular interactions that determine the gas-phase composition are the same for solvent molecules as they are for solute molecules; the vapor pressures of the solvent and the solute are the same; the gas above the solution has the same composition as the solution; the partial pressure of the solute is proportional to the solute concentration, \(y_A\); the proportionality constant is the pure-solvent vapor pressure, \(P^{\textrm{⦁}}_A\); and the solution obeys Raoult’s law. However, if the intermolecular forces are not all the same, their net effect changes as the solute concentration changes. As the solute concentration increases, the effects of solute–solute interactions become increasingly important. If these are different from the effects of solute–solvent and solvent–solvent interactions, the solute partial pressure is not proportional to the solute concentration.
Conversely, at some sufficiently low concentration, solute molecules are so far apart that the effects of solute–solute interactions become negligible. Only solute–solvent and solvent–solvent interactions affect the solute vapor pressure. Because these remain constant as the solute concentration decreases further, the solute partial pressure is proportional to the solute concentration in this low-concentration regime. However, if the effects of solute–solvent interactions are different from those of solvent–solvent interactions, the pure-solvent vapor pressure, \(P^{\textrm{⦁}}_A,\) is not the proportionality constant.
We can assume the existence of a hypothetical ideal gas state for any substance, even a substance that has no measureable vapor pressure at any attainable temperature. We can assume that the substance has a well-defined Gibbs free energy of formation in this state even though there may be no possibility of measuring its value. Likewise, we can assume that any solute exerts some partial pressure over its solution. We consider that this partial pressure has some finite value, even if it is much too small to measure. It follows that the fugacity of the solute has a finite value. Henry’s law implies that the fugacity is proportional to the solute concentration, at least in the limit of arbitrarily low concentration. Expressing the concentration of solute A as its mole fraction, we have
\[f_A\left(P,y_A,y_B\right)={P_A}/{P^o}={x_AP}/{P^o}={{\kappa }_Ay_A}/{P^o} \nonumber \]
and the chemical potential of the solute is
\[{\mu }_A\left(P,y_A,y_B\right)={\Delta }_fG^o\left(A,{HIG}^o\right)+RT{ \ln f_A\ }\left(P,y_A,y_B\right) \nonumber \]
If the solute behaves ideally in the gas phase, Henry’s law leads to simple expressions for its chemical potential and activity. The development of these expressions is very similar to the corresponding development from Raoult’s law. The essential differences arise from the introduction of a different standard state for the activity of the solute. We begin with our basic equation for the chemical potential of\(\ A\) in the gas phase: \[{\mu }_A\left(g,P,x_A,x_B\right)={\Delta }_fG^o\left(A,{HIG}^o\right)+RT{ \ln \left[\frac{x_AP}{P^o}\right]\ }+\int^P_0{\left(\frac{{\overline{V}}_A\left(g\right)}{RT}-\frac{1}{P}\right)}dP \nonumber \]
The integral term vanishes because we assume ideal gas behavior. We write \({\tilde{a}}_A\left(\mathrm{solute},P,y_A,y_B\right)\) to represent the activity of \(A\) in a solution at pressure \(P\) and in which the composition is specified by the mole fractions \(y_A\) and \(y_B\).
We choose a hypothetical liquid to be the standard state for the activity of the solute. This hypothetical liquid is pure liquid \(A\) at the vapor pressure it would exhibit if it followed Henry’s law over the entire range of possible system compositions. This pressure is equal to its Henry’s law constant \({\kappa }_A\). (See Figure 5.) Let us denote the chemical potential of this standard state by \({\widetilde{\mu }}^o_A\left(Hyp\ \ell ,{\kappa }_A\right)\). The chemical potential of solute \(A\) and the activity of \(A\) in the solution are related by
\[{\mu }_A\left(P,y_A,y_B\right)={\widetilde{\mu }}^o_A\left(Hyp\ \ell ,{\kappa }_A\right)+RT{ \ln {\tilde{a}}_A\ }\left(P,y_A,y_B\right) \nonumber \]
and since \({\mu }_A\left(g,P,x_A,x_B\right)={\mu }_A\left(P,y_A,y_B\right)\), and the gas is ideal, we have
\[{ \ln \left[{\tilde{a}}_A\left(P,y_A,y_B\right)\right]\ }=\frac{{\Delta }_fG^o\left(A,{HIG}^o\right)-{\widetilde{\mu }}^o_A\left(Hyp\ \ell ,{\kappa }_A\right)}{RT}+{ \ln \left[\frac{x_AP}{P^o}\right]\ } \nonumber \]
Except for the solute standard state, this is same as the equation that we develop in Section 16.1.
This equation must give the activity of solute \(A\) in its standard state, which is pure hypothetical liquid at a pressure equal to the Henry’s law constant: \(P=P_A={\kappa }_A\). In this state, \(x_A=y_A=1\) and \(x_B=y_B=0\). In its standard state, the activity of solute \(A\) is unity; we have \({\tilde{a}}_A\left(P,y_A,y_B\right)={\tilde{a}}_A\left({\kappa }_A,1,0\right)=1\). Making these substitutions and rearranging, we find
\[\frac{{\Delta }_fG^o\left(A,{HIG}^o\right)-{\widetilde{\mu }}^o_A\left(Hyp\ \ell ,{\kappa }_A\right)}{RT}=-{ \ln \left[\frac{{\kappa }_A}{P^o}\right]\ } \nonumber \]
Substituting this result into our general equation for \({ \ln \left[{\tilde{a}}_A\left(\mathrm{solute},P,y_A,y_B\right)\right]\ }\), we find that the activity of solute \(A\) is \[{\tilde{a}}_A\left(P,y_A,y_B\right)=\frac{x_AP}{{\kappa }_A} \nonumber \] (any solution, ideal gas)
The chemical potential of the standard-state hypothetical pure liquid whose vapor pressure at \(T\) is \({\kappa }_A\) is
\[{\widetilde{\mu }}^o_A\left(Hyp\ \ell ,{\kappa }_A\right)={\Delta }_fG^o\left(A,{HIG}^o\right)+RT{ \ln \left[\frac{{\kappa }_A}{P^o}\right]\ } \nonumber \]
This is a general result for the activity of solute \(A\) when the standard state is the hypothetical pure liquid whose pressure is \({\kappa }_A\), and \(A\) behaves ideally in the gas phase. If Henry’s law is obeyed, we have \(x_AP=y_A{\kappa }_A\). Substituting, we find
\[{\tilde{a}}_A\left(P,y_A,y_B\right)=y_A \nonumber \] (Henry’s law is obeyed)
The Henry’s law development and the Raoult’s law development give the same value for the chemical activity. However, the standard states are different.
If the solute obeys Raoult’s law, the standard state we choose for the solute is the pure solute at its equilibrium vapor pressure; in this state, the pure solute is in equilibrium with its own gas. Real substances can satisfy this condition. If the solute obeys Henry’s law, the standard state we choose for the solute is a hypothetical pure-liquid solute at a pressure equal to \({\kappa }_A\). In this state, we assume that the hypothetical liquid is in equilibrium with its own gas, also at pressure \({\kappa }_A\). The hypothetical standard-state liquid is a substance in which the interactions among \(A\) molecules have the same effects as the interactions, in a very dilute solution, between \(A\) molecules and the \(B\) molecules that comprise the solvent. If solutions of \(A\) and \(B\) are described poorly by Raoult’s law, the vapor pressure of pure liquid \(A\), \(P^{\textrm{⦁}}_A\), is likely to be very different from the vapor pressure, \({\kappa }_A\), of the hypothetical standard-state liquid that we define using Henry’s law.
Our development produces a model for the chemical potential of the solute in which the activity is equal to the solute mole fraction. At the same mole fraction, every solute has the same activity. The chemical potentials of different solutes vary because the chemical potential in its standard state is different for every solute. We conclude that we can let \({\tilde{a}}_A=y_A\) for any sufficiently dilute solute, even when it is not feasible to measure the chemical potential of the solute in its standard state experimentally.


