14.12: Relating Fugacity and Chemical Activity
- Page ID
- 152680
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)While we develop the fugacity concept by thinking about the Gibbs free energy of a pure real gas, our definition means that the fugacity of a substance in any system depends only on the difference between the chemical potential in that system and its chemical potential in the standard state. There is no reason to confine the definition of fugacity to gaseous systems. We generalize it: Our defining relationship specifies the fugacity of any substance in any system as a function of the difference between its chemical potential in that system and its chemical potential in its hypothetical ideal gas standard state.
Since the Gibbs free energy of an arbitrary system depends on the pressure, temperature, and composition of the system, the fugacity of any component also depends on these variables. However, there is an additional constraint on the fugacity. At a sufficiently low system pressure, the gases in any system behave ideally, and they obey Boyle’s law of partial pressures; the integral in the fugacity-coefficient equation becomes zero, and the fugacity coefficient becomes unity. In the limit as \(P\to 0\), \(f_A\to x_AP\), where \(x_A\) is the mole fraction of \(A\) in the gas phase. At a sufficiently low pressure, any gas mixture behaves ideally, and the fugacity of a constituent species becomes equal to its gas-phase partial pressure. (For a mixture of ideal gases, the fugacity of a component is always equal to its partial pressure.)
In Section 14.10, we define the activity of component A in an arbitrary system by the relationship
\[{\mu }_A={\widetilde{\mu }}^o_A+RT{ \ln \left[{\tilde{a}}_A\left(P,T,c_A,c_B,c_C,\dots \right)\right]\ } \nonumber \]
where \({\widetilde{\mu }}^o_A\) is the chemical potential of \(A\) in an activity standard state in which we stipulate that the activity of \(A\) is unity. Since the defining equations for activity and for fugacity are formally identical, the distinction between activity and fugacity lies in our choices of standard states and in the facts that activity is dimensionless while fugacity has the units of pressure. If we use the hypothetical ideal-gas standard state for activity and measure the concentration in bars, the practical distinction between activity and fugacity vanishes. We can view the fugacity as a specialization of the activity concept.
In summary: The fugacity function proves to be a useful way to express the difference between the chemical potential of a substance in two different states. Fugacity is measured in bars with the hypothetical ideal gas standard state as the reference state. We add chemical activity to our list of useful thermodynamic properties because it extends the advantages of the fugacity representation to non-volatile components of systems that contain condensed phases. The standard state for activity can be any particular state of any convenient system that contains the substance. We define the activity of the substance in this reference system to be unity. (As with the hypothetical ideal gas standard state, we often find it useful to define a hypothetical system as the standard state for the activity.) The chemical potential of the substance in the standard-state system is, by definition, the standard chemical potential, \({\widetilde{\mu }}^o_A\), for this particular activity scale.
In the remainder of this chapter and in Chapters 15-17, we consider additional properties and applications of fugacity and chemical activity. Before doing so however, we digress to observe that we can choose an alternate definition of activity: chemical activity can be defined as a ratio of fugacities. Let us consider three systems that contain substance \(A\).
The first is pure gas \(A\) in its hypothetical ideal gas standard state at temperature \(T\), \(A\left({HIG}^o,T\right)\). In this state, the fugacity of \(A\) is unity, \(f_A\left({HIG}^o,T\right)=1\ \mathrm{bar}\). The chemical potential of \(A\) is the standard-state chemical potential, which we equate to the Gibbs free energy of formation:
\[{\overline{G}}_A\left({HIG}^o,T\right)={\Delta }_fG^o\left(A,{HIG}^o,T\right)={\mu }^o_A \nonumber \]
The second is a system that we define as the standard state for the activity of \(A\) at temperature \(T\). Apart from convenience, there is no reason to prefer any particular system for this role. We denote this system as \(A\left(activity\ standard\ state,T\right)\) or, for short, \(A\left(ss,T\right)\). By definition, the activity of \(A\) in this state is unity, \({\tilde{a}}^o_A\left(ss\right)=1\), and the chemical potential of \(A\) in this system is the standard chemical potential for this particular activity scale: \({\overline{G}}_A\left(ss,T\right)={\widetilde{\mu }}^o_A\). We denote the fugacity of \(A\) in this state as \(f_A\left(ss\right)\). By our definition of fugacity, we have
\[{\widetilde{\mu }}^o_A={\mu }^o_A+RT{ \ln \left[\frac{f_A\left(ss\right)}{f_A\left({HIG}^o\right)}\right]\ } \nonumber \]
The third is an arbitrary system that we denote as \(A\left(P,T,c_A,c_B,c_C,\dots \right)\). We denote the chemical potential, fugacity, and activity of \(A\) in this system as \({\overline{G}}_A\left(P,T,c_A,c_B,c_C,\dots \right)={\mu }_A\left(P,T,c_A,c_B,c_C,\dots \right)\), \(f_A\left(P,T,c_A,c_B,c_C,\dots \right)\), and \({\tilde{a}}_A\left(P,T,c_A,c_B,c_C,\dots \right)\), respectively. By our definition of fugacity, we have
\[{\mu }_A\left(P,T,c_A,c_B,c_C,\dots \right)={\mu }^o_A+RT{ \ln \left[\frac{f_A\left(P,T,c_A,c_B,c_C,\dots \right)}{f_A\left({HIG}^o\right)}\right]\ } \nonumber \]
and by our definition of activity,
\[{\mu }_A\left(P,T,c_A,c_B,c_C,\dots \right)={\widetilde{\mu }}^o_A+RT{ \ln \left[{\tilde{a}}_A\left(P,T,c_A,c_B,c_C,\dots \right)\right]\ } \nonumber \]
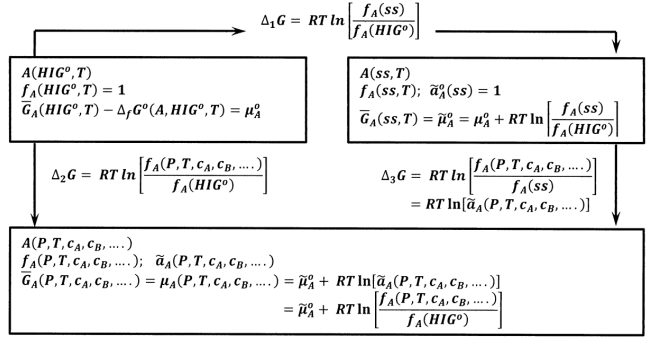
Figure 2 summarizes the relationships among the Gibbs free energies of these three states of substance \(A\). From the cycle in Figure 2, we have \({\Delta }_1G+{\Delta }_3G={\Delta }_2G\), so that
\[RT{ \ln \left[\frac{f_A\left(ss,T\right)}{f_A\left({HIG}^o\right)}\right]+RT{ln \left[\frac{f_A\left(P,T,c_A,c_B,\dots .\right)}{f_A\left(ss,T\right)}\right]\ }\ } \nonumber \] \[=RT{ \ln \left[\frac{f_A\left(P,T,c_A,c_B,c_C,\dots \right)}{f_A\left({HIG}^o\right)}\right]\ } \nonumber \] \[=RT{ \ln \left[{\tilde{a}}_A\left(P,T,c_A,c_B,\dots .\right)\right]\ } \nonumber \]
and \[{\tilde{a}}_A\left(P,T,c_A,c_B,c_C,\dots \right)=\frac{f_A\left(P,T,c_A,c_B,c_C,\dots \right)}{f_A\left(ss,T\right)} \nonumber \]
That is, the activity of a substance in a particular system is always equal to its fugacity in that system divided by its fugacity in the standard state for activity. From this relationship, it is evident that activity is always a dimensionless function of concentrations.


