12.6: Phase Equilibria - Temperature Dependence of the Boiling Point

In Sections 12.4 and 12.6, we explore two approaches to using the entropy-based criterion for spontaneous change. In discussing the melting of ice at \(\mathrm{+10}\) C, we calculate the entropy changes for both the system and the surroundings to show that \(\Delta S_{universe}>0\), as the second law requires for a spontaneous process. In discussing the pressure-dependence of a liquid’s boiling point in Section 12.6, we relate the second law criterion for spontaneous change to Le Chatelier’s principle. We turn now to specifying the pressures and temperatures at which two phases of a pure substance are in equilibrium. When we choose pressure and temperature as the independent variables, the Gibbs free energy criteria specify the equilibrium state and the direction of spontaneous change.

For a reversible process in which all the work is pressure–volume work and in which the pressure and temperature change by \(dP\) and \(dT\), the change in the Gibbs free energy is \(dG=VdP-SdT\). Let us apply this relationship to the liquid–vapor equilibrium problem that we discuss in Section 12.6. To do so, we view the process from a slightly different perspective. We suppose that we have two systems. These are identical to the initial and final states of the system in our discussion above. One of these systems is at liquid–vapor equilibrium at a particular pressure, \(P\), and temperature,\(\ T\). The other is at liquid–vapor equilibrium at \(P+dP\) and \(T+dT\). We consider the change in the Gibbs free energy of a mole of the substance as it reversibly traverses the cycle sketched in Figure 4.

Figure 4. Molar Gibbs free energy differences between two liquid-vapor equilibrium states.

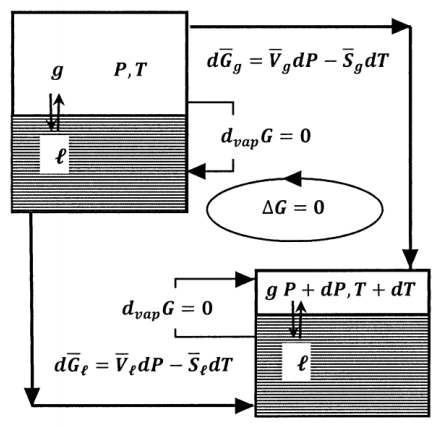
The pressure and temperature are constant in each of the two equilibrium states. In either of these equilibrium states, the Gibbs free energy does not change when a mole of liquid is converted to its gas, \({\Delta }_{vap}G\left(P,T\right)=0\) and \({\Delta }_{vap}G\left(P+dP,T+dP\right)=0\). When the pressure and temperature of one mole of liquid change from \(P\) and \(T\) to \(P+dP\) and \(T+dT\), the Gibbs free energy change is \(d\overline{G}\left(\ell \right)=\overline{V}_{\ell }dP- \overline{S}_{\ell }dT\). For a mole of gas, this change in the pressure and temperature change the Gibbs free energy by \(d\overline{G}\left(g\right)= \overline{V}_gdP- \overline{S}_gdT\). (\(\overline{V}_{\ell }\), \(\overline{V}_g\), \(\overline{S}_{\ell }\), and \(\overline{S}_g\) are evaluated at \(P\) and \(T\). However, since \(dP\) and \(dT\) are small, these quantities are essentially constant over the pressure and temperature ranges involved.) For the individual steps in this cycle, we have

\[\left(\ell ,\ P,\ T\right)\to \left(\ell ,\ P+dP,\ T+dT\right) d\overline{G}\left(\ell \right)=\overline{V}_{\ell }dP- \overline{S}_{\ell }dT \nonumber \]

\[\left(\ell ,\ P+dP,\ T+dT\right)\to \left(g,\ P+dP,\ T+dT\right) {\Delta }_{vap}G\left(P+dP,T+dT\right)=0 \nonumber \]

\[\left(g,\ P+dP,\ T+dT\right)\to \left(g,\ P,\ T\right) -d\overline{G}\left(g\right)=-\left(\overline{V}_gdP- \overline{S}_gdT\right) \nonumber \]

\[\left(g,\ P,\ T\right)\to \left(\ell ,\ P,\ T\right) -{\Delta }_{vap}G\left(P,T\right)=0 \nonumber \]

Since the Gibbs free energy is a state function, the sum of these terms is zero. We have

\[{\Delta }_{vap}G\left(P+dP,T+dT\right)-{\Delta }_{vap}G\left(P,T\right) +d\overline{G}\left(\ell \right)-d\overline{G}\left(g\right) =d\overline{G}\left(\ell \right) -d\overline{G}\left(g\right) =0 \nonumber \]

so that \(d\overline{G}\left(\ell \right)=d\overline{G}\left(g\right)\). That is, the Gibbs free energy of the liquid changes by the same amount as the Gibbs free energy of the gas when a mole of either is taken from one liquid–vapor equilibrium state to another. Substituting, we find a condition that the pressure and temperature changes must satisfy when the system goes from the liquid–vapor equilibrium state at \(\left(P,T\right)\) to the liquid–vapor equilibrium state at \(\left(P+dP,T+dT\right)\):

\[\left( \overline{V}_g- \overline{V}_{\ell }\right)dP-\left(\overline{S}_g-\overline{S}_{\ell }\right)dT=0 \nonumber \]

We let \({\Delta }_{vap}\overline{V}= \overline{V}_g- \overline{V}_{\ell }\) and \({\Delta }_{vap}\overline{S}=\overline{S}_g-\overline{S}_{\ell }\), where \({\Delta }_{vap}\overline{V}\) and \({\Delta }_{vap}\overline{S}\) are the volume and entropy changes that accompany the vaporization of one mole of the liquid at \(P\) and \(T\). \({\Delta }_{vap}\overline{V}\) and \({\Delta }_{vap}\overline{S}\) are essentially constant over the small pressure and temperature ranges involved. Substituting, we have \({\Delta }_{vap}\overline{V}dP-{\Delta }_{vap}\overline{S}dT=0\), which we can rearrange to give

\[\frac{dP}{dT}=\frac{\Delta _{vap}\overline{S}}{\Delta _{vap}\overline{V}} \nonumber \]

As one mole of liquid vaporizes reversibly at \(P\) and \(T\), the system accepts heat \(q^{rev}_P=\Delta _{vap}\overline{H}\). Hence, the entropy of vaporization at \(P\) and \(T\) is \({\Delta }_{vap}\overline{S}={\Delta }_{vap}\overline{H}/T\), and the relationship between \(dP\) and \(dT\) becomes

\[\frac{dP}{dT}=\frac{\Delta _{vap}\overline{H}}{T \Delta _{vap}\overline{V}} \nonumber \]

Below we see that such a relationship holds for any equilibrium between two pure phases. The general relationship is called the Clapeyron equation.

This analysis is successful because the constituents are pure phases; the properties of the liquid are independent of how much vapor is present and vice versa. When we analyze the equilibrium between a liquid solution and a gas of the solution’s components, the problem is more complex, because the properties of the phases depend on their compositions.