10.14: The Joule-Thomson Effect
- Page ID
- 152344
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)In practice, the Joule-Thomson experiment is done by allowing gas from a pressure vessel to pass through an insulated tube. The tube contains a throttling valve or a porous plug through which gas flows slowly enough so that the gas upstream from the plug is at a uniform pressure \(P_{\mathrm{1}}\), and the gas downstream is at a uniform pressure \(P_{\mathrm{2}}\). In general, the temperature of the downstream gas is different from that of the upstream gas. Depending on the initial temperature and pressure, the pressure drop, and the gas, the temperature of the gas can either decrease or increase as it passes through the plug. (We see below that it must be constant if the gas is ideal.)
The temperature change is called the Joule-Thomson effect. The enthalpy of the gas remains constant. If the measured temperature and pressure changes are \(\mathrm{\Delta }T\) and \(\mathrm{\Delta }P\), their ratio is called the Joule-Thomson coefficient, \({\mu }_{JT}\). We define
\[\mathrm{\ }{\mu }_{JT} = {\left(\frac{\partial T}{\partial P}\right)}_H\mathrm{\approx }\frac{\mathrm{\Delta }T}{\mathrm{\Delta }P} \nonumber \]
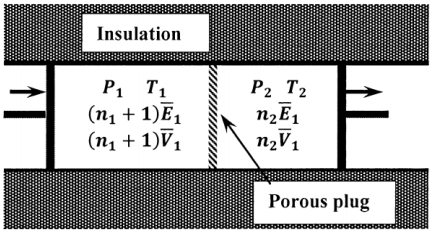
To see that the enthalpy of the gas is the same on both sides of the plug, we consider an idealized version of the experiment, in which the flow of gas through the plug is controlled by the coordinated movement of two pistons. (See Figure 3.) We suppose that the gas is pushed through the plug in such a way that the upstream pressure remains constant at \(P_1\) and the downstream pressure remains constant at \(P_2\). Let us consider the changes that result when one mole of gas passes through the plug under these conditions. Initially, there are \(n_1+1\) moles of gas on the upstream side at a pressure \(P_1\), occupying a volume \(\left(n_1+1\right){\overline{V}}_1\), at a temperature \(T_1\), and having an energy per mole of \({\overline{E}}_1\). On the downstream side, there are \(n_2\) moles of gas at a pressure \(P_2\), occupying a volume \(n_2{\overline{V}}_2\), but having a temperature \(T_2\) and an energy per mole of \({\overline{E}}_2\).
When the process is complete, there are \(n_1\) moles of gas on the upstream side, still at a pressure \(P_1\) and temperature \(T_1\), but occupying a volume \(n_1{\overline{V}}_1\). On the downstream side, there are \(n_2+1\) moles of gas at pressure \(P_2\), occupying volume \(\left(n_2+1\right){\overline{V}}_2\) at a temperature \(T_2\) and with an energy per mole of \({\overline{E}}_2\). On the upstream side, \(\Delta E_1=-\overline{E}_1\) and \(w_1=-P_1\left[n_1 \overline{V}_1-\left(n_1+1\right) \overline{V}_1 \right]=P_1 \overline{V}_1\)
On the downstream side, \(\Delta E_2={\overline{E}}_2\), and
\[w_2=-P_2\left[\left(n_2+1\right){\overline{V}}_1-n_2{\overline{V}}_1\right]=-P_2{\overline{V}}_2 \nonumber \]
Since the process is adiabatic, any heat taken up by the upstream gas must be surrendered by the downstream gas, so that \(q_1+q_2=0\). For the process of moving the mole of gas across the plug,
\[\Delta E=\Delta E_1+\Delta E_2=-\overline{E}_1+\overline{E}_2=q_1+q_2+w_1+w_2=P_1\overline{V}_1-P_2\overline{V}_2 \nonumber \]
from which
\[{\overline{E}}_1+P_1{\overline{V}}_1={\overline{E}}_2+P_2{\overline{V}}_2 \nonumber \] or \[{\overline{H}}_1={\overline{H}}_2 \nonumber \]
so that we have \(\Delta H=0\) for the expansion.
In practice, it is convenient to measure downstream pressures and temperatures, \(P_2\) and \(T_2\), in a series of experiments in which the upstream pressure and temperature, \(P_1\) and \(T_1\), are constant. The enthalpy of the gas is the same at each of these pressure-temperature points. A graph of these points is an isenthalpic (constant enthalpy) curve. At any given pressure and temperature, the Joule-Thomson coefficient, \({\mu }_{JT}\), is the slope of this curve.
We can also express \(\mathrm{\ }{\mu }_{JT}\) as a function of the heat capacity, \(C_P\), and the coefficient of thermal expansion, \(\alpha\), where \(\alpha =V^{-1}{\left({\partial V}/{\partial T}\right)}_P\). We begin by expressing \(d\overline{H}\) as a function of temperature and pressure:
\[d\overline{H}={\left(\frac{\partial \overline{H}}{\partial T}\right)}_PdT+{\left(\frac{\partial \overline{H}}{\partial P}\right)}_TdP \nonumber \]
If we divide through by \(dP\) and hold \(\overline{H}\) constant, we obtain
\[0={\left(\frac{\partial \overline{H}}{\partial T}\right)}_P{\left(\frac{\partial T}{\partial P}\right)}_{\overline{H}}+{\left(\frac{\partial \overline{H}}{\partial P}\right)}_T \nonumber \]
so that
\[{\mu }_{JT}={\left(\frac{\partial T}{\partial P}\right)}_{\overline{H}}=-{{\left(\frac{\partial \overline{H}}{\partial P}\right)}_T}/{{\left(\frac{\partial \overline{H}}{\partial T}\right)}_P}=-\frac{1}{C_P}{\left(\frac{\partial \overline{H}}{\partial P}\right)}_T \nonumber \]
If we substitute the coefficient of thermal expansion into the expression for \({\left({\partial \overline{H}}/{\partial P}\right)}_T\) that we develop in Section 10.5, we have
\[{\left(\frac{\partial \overline{H}}{\partial P}\right)}_T=\overline{V}-T{\left(\frac{\partial \overline{V}}{\partial T}\right)}_P=\overline{V}-\alpha \overline{V}T=\overline{V}\left(1-\alpha T\right) \nonumber \]
For an ideal gas, \({\left({\partial \overline{V}}/{\partial T}\right)}_P={\overline{V}}/{T}\), so that both \({\left({\partial \overline{H}}/{\partial P}\right)}_T\) and \({\mu }_{JT}\) are zero. For real gases, we substitute into the expression for \({\mu }_{JT}\) to find
\[{\mu }_{JT}={\left(\frac{\partial T}{\partial P}\right)}_{\overline{H}}=-\frac{1}{C_P}{\left(\frac{\partial \overline{H}}{\partial P}\right)}_T=-\frac{\overline{V}}{C_P}\left(1-\alpha T\right) \nonumber \]
Given \(\overline{V}\) and any two of \({\mu }_{JT}\), \(C_P\), or \(\alpha\), we can find the third from this relationship.
Making the same substitutions using the partial derivatives we found above for a van der Waals gas, we find
\[{\mu }_{JT}=-\frac{1}{C_P}\left(\overline{V}-\frac{RT}{\gamma \left(P,\overline{V}\right)}\right) \nonumber \]
Given that the van der Waals equation oversimplifies the effects of intermolecular forces, we can anticipate that calculation of the Joule-Thomson coefficient from the van der Waals parameters is likely to be qualitatively correct, but in poor quantitative agreement with experimental results. Figure 4 compares calculated and experimental curves for the Joule-Thomson coefficient of nitrogen gas at 0 C from 1 to 200 bar. (Calculated values take \(a=0.137\mathrm{\ Pa}\ {\mathrm{m}}^{\mathrm{6}}\mathrm{\ }{\mathrm{mol}}^{--\mathrm{2}}\) and \(b=3.81\times {10}^{-5}\ {\mathrm{m}}^{\mathrm{3}}\mathrm{\ }{\mathrm{mol}}^{--\mathrm{1}}\). The experimental data are from reference 1.)

We anticipate that the Joule-Thomson coefficient becomes zero at pressures and temperatures where the effects of intermolecular attractions and repulsions exactly offset one another. For interactions between molecules, attractive forces have the dominant effect at long distances, while repulsive forces dominate at short distances. The lower the pressure, the greater the average distance between gas molecules. Therefore, at any given temperature and a sufficiently low pressure, the effects of intermolecular attractive forces are more important than those of intermolecular repulsive forces. At low pressures, the Joule-Thomson coefficient should be positive. As the pressure increases, the effects of both attractive and repulsive forces must both increase, but at a sufficiently high pressure, the average intermolecular distance becomes so small that the effects of intermolecular repulsive forces become dominant. Therefore, we anticipate that the Joule-Thomson coefficient decreases as the pressure increases, eventually becoming negative.
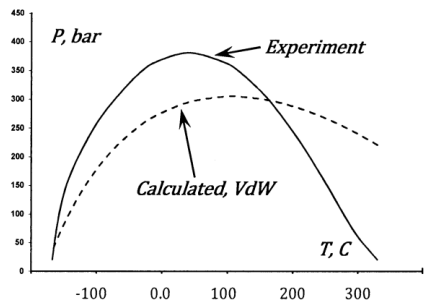
Experiments confirm these expectations. A temperature and pressure at which the Joule-Thomson coefficient becomes zero is called a Joule-Thomson inversion point. The experimentally determined curve for nitrogen gas\({}^{1}\) is graphed in Figure 5. The van der Waals model also exhibits this effect. The inversion curve can be found from the expression for \({\mu }_{JT}\) developed above for a van der Waals gas. The inversion curve for nitrogen that is found in this way is also graphed in Figure 5. Qualitatively, the agreement is a satisfying confirmation of the basic interpretation that we have given for the role of intermolecular forces. Quantitatively, the agreement is poor, as we expect given the overly simple character of the van der Waals model.
The Joule-Thomson coefficient for an ideal gas is zero, and we normally expect the properties of real gases to approach those of an ideal gas as the pressure falls to zero. However, both experiment and the van der Waals model indicate that the Joule-Thomson coefficient converges to a finite value as the pressure decreases to zero at a fixed temperature. A statistical thermodynamic model\({}^{2}\) also predicts this outcome. This model calculates the coefficients in the virial equation of state. In it, the second virial coefficient reflects the net effect of attractive and repulsive forces between a pair of molecules, and it is the second virial coefficient and its temperature derivative determine that the value of \({\left({\partial \overline{H}}/{\partial P}\right)}_T\). (Higher-order virial coefficients reflect interactions among larger numbers of molecules.)


