8.10: Problems
- Page ID
- 152073
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)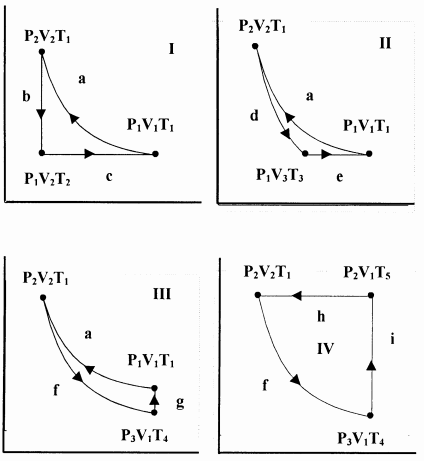
1. One mole of an ideal gas reversibly traverses Cycle I above. Step a is isothermal. Step b is isochoric (constant volume). Step c is isobaric (constant pressure). Assume \(C_V\) and \(C_P\) are constant. Find \(q\), \(w\), \(\Delta E\), and \(\Delta H\) for each step and for the cycle. Prove \(C_P=C_V+R\).
2. One mole of an ideal gas reversibly traverses Cycle II below. Step a is the same isothermal process as in problem 1. Step d is adiabatic. Step e is isobaric. Assume \(C_V\) and \(C_P\) are constant. Find \(q\), \(w\), \(\Delta E\), and \(\Delta H\) for each step and for the cycle.
3. One mole of an ideal gas reversibly traverses Cycle III below. Step a is the same isothermal process as in
problem 1. Step f is adiabatic. Step g is isochoric. Assume \(C_V\) and \(C_P\) are constant. Find \(q\), \(w\), \(\Delta E\), and \(\Delta H\) for each step and for the cycle.
4. One mole of an ideal gas reversibly traverses Cycle IV. Step h is isobaric. Step f is the same adiabatic process as in problem 3. Step i is isochoric. Assume \(C_V\) and \(C_P\) are constant. Find \(q\), \(w\), \(\Delta E\), and \(\Delta H\) for each step and for the cycle.
5. Prove that the work done on the system is positive when the system traverses Cycle I. Note that Cycle I traverses the region of the \(PV\) plane that it encloses in a counter-clockwise direction. Hint: Note that \(T_2<t_1\). Show that \({V_2}/{V_1}={T_2}/{T_1}\).
6. Cycles III and IV share a common adiabatic step. Express the work done in each of these cycles in terms of \(V_1\), \(V_2\), and \(T_1\). Prove that the work done in Cycle IV is greater than the work done in Cycle III.
7. Cycles I, II, and III share a common first step, a. Express \(V_3\), \(T_3\), and \(T_4\) in terms of \(V_1\), \(V_2\), and \(T_1\). For \(V_1=10\ \mathrm{L}\), \(V_2=2\ \mathrm{L}\), and \(T_1=400\ \mathrm{K}\), show that the work done decreases in the order Cycle I \(\mathrm{>}\) Cycle III \(\mathrm{>}\) Cycle II.
8. For water, the enthalpies of fusion and vaporization are \(6.009\) and \(40.657\ \mathrm{k}\mathrm{J}\ {\mathrm{mol}}^{-1}\), respectively. The heat capacity of liquid water varies only weakly with temperature and can be taken as \(\mathrm{75.49\ }\mathrm{J}\ {\mathrm{mol}}^{-1}\ {\mathrm{K}}^{-1}\). The heat capacity of water vapor varies with temperature: \[C_P\left(H_2O\mathrm{,\ g}\right)=30.51+\left(1.03\times {10}^{-2}\right)T \nonumber \] where \(T\) is in degrees K and the heat capacity is in \(\mathrm{J}\ {\mathrm{mol}}^{-1}\ {\mathrm{K}}^{-1}\). Estimate the enthalpy of sublimation of water.
9. If we truncate the virial equation \(\left(Z=1+B^*\left(T\right)P+\dots \right)\) and make use of \(B\left(T\right)=RTB^*\left(T\right)\), where\(\ B\left(T\right)\) is the “second virial coefficient” most often given in data tables, the molar volume is \[\overline{V}=\frac{RT}{P}+B\left(T\right) \nonumber \] Show that \[{\left(\frac{\partial H}{\partial P}\right)}_T=B\left(T\right)-T\left(\frac{dB}{dT}\right) \nonumber \]
The Handbook of Chemistry and Physics (CRC Press, 79\({}^{th}\) Ed., 1999, p. 6–25) gives the temperature dependence of \(B\) for water vapor as
\[B=-1158-5157t-10301t^2-10597t^3-4415t^4 \nonumber \]
where \(t=\left({298.15}/{T}\right)-1\), \(T\) is in degrees kelvin, and the units of \(B\) are \({\mathrm{cm}}^{-3\ }{\mathrm{mol}}^{-1}\). Estimate the enthalpy change when one mole of water vapor at 1 atm and 100 C is expanded to the equilibrium sublimation pressure, which for this purpose we can approximate as the triple-point pressure, \(610\ \mathrm{Pa}\). How does this value compare to the result of problem 8?
10. The heat capacities of methanol liquid and gas are \(81.1\) and \(44.1\ \mathrm{J}\ {\mathrm{mol}}^{-1}\ {\mathrm{K}}^{-1}\), respectively. The second virial coefficient for methanol vapor is
\[B=-1752-4694t \nonumber \]
where \(t=\left({298.15}/{T}\right)-1\), \(T\) is in degrees kelvin, and the units of \(B\) are \({\mathrm{cm}}^{-3\ }{\mathrm{mol}}^{-1}\). Referring to the discussion of methanol vaporization in §5, calculate \({\Delta }_{\left(1\right)}H\), \({\Delta }_{\left(4\right)}H\), \({\Delta }_{\left(5\right)}H\), \({\Delta }_{\left(vap\right)}H^o\). Compare this value of \({\Delta }_{\left(vap\right)}H^o\) to the value given in the text. [Data from the Handbook of Chemistry and Physics, CRC Press, 79\({}^{th}\) Ed., 1999, p. 5-27 and p. 6-31.]
| Molecular formula | Name | \({\Delta }_fH^o\)\(\left(\mathrm{k}\mathrm{J}\ {\mathrm{mol}}^{-1}\right)\) |
| \(H_2O\ \left(\mathrm{liq}\right)\) | Water | \(-285.8\) |
| \(CO\ \left(\mathrm{g}\right)\) | Carbon monoxide | \(-110.5\) |
| \(CO_2\ \left(\mathrm{g}\right)\) | Carbon dioxide | \(-393.5\) |
| \(CH_4\left(\mathrm{g}\right)\) | Methane | \(-74.6\) |
| \(C_2H_4\left(\mathrm{g}\right)\) | Ethylene | \(52.4\) |
| \(C_2H_6\left(\mathrm{g}\right)\) | Ethane | \(-84.0\) |
| \(CH_3CH_2OH\ \left(\mathrm{liq}\right)\) | Ethanol | \(-277.6\) |
| \(CH_3CHO\ \left(\mathrm{liq}\right)\) | Acetaldehyde | \(-192.2\) |
| \(CH_3CO_2H\ \left(\mathrm{liq}\right)\) | Acetic acid | \(-484.3\) |
| \(CH_3CH_2CHO\ \left(\mathrm{liq}\right)\) | Propanal | \(-215.6\) |
| \(C_6H_6\ \left(\mathrm{liq}\right)\) | Benzene | \(49.1\) |
| \(C_6H_5CO_2H\ \left(\mathrm{s}\right)\) | Benzoic acid | \(-385.2\) |
11. Using data from the table above, find the enthalpy change for each of the following reactions at 298 K.
(a) \(C_2H_6\left(\mathrm{g}\right)+
Callstack:
at (Bookshelves/Physical_and_Theoretical_Chemistry_Textbook_Maps/Thermodynamics_and_Chemical_Equilibrium_(Ellgen)/08:_Enthalpy_and_Thermochemical_Cycles/8.10:_Problems), /content/body/p[19]/span, line 1, column 1
(b) \(C_2H_4\left(\mathrm{g}\right)+
Callstack:
at (Bookshelves/Physical_and_Theoretical_Chemistry_Textbook_Maps/Thermodynamics_and_Chemical_Equilibrium_(Ellgen)/08:_Enthalpy_and_Thermochemical_Cycles/8.10:_Problems), /content/body/p[20]/span, line 1, column 1
(c) \(C_2H_6\left(\mathrm{g}\right)+
Callstack:
at (Bookshelves/Physical_and_Theoretical_Chemistry_Textbook_Maps/Thermodynamics_and_Chemical_Equilibrium_(Ellgen)/08:_Enthalpy_and_Thermochemical_Cycles/8.10:_Problems), /content/body/p[21]/span, line 1, column 1
(d) \(C_6H_6\left(\mathrm{liq}\right)+\ CO_2\left(\mathrm{g}\right)\to C_6H_5CO_2H\left(\mathrm{s}\right)\)
(e) \(CH_3CHO\left(\mathrm{liq}\right)+
Callstack:
at (Bookshelves/Physical_and_Theoretical_Chemistry_Textbook_Maps/Thermodynamics_and_Chemical_Equilibrium_(Ellgen)/08:_Enthalpy_and_Thermochemical_Cycles/8.10:_Problems), /content/body/p[23]/span, line 1, column 1
(f) \(CH_4\left(\mathrm{g}\right)+H_2O\left(\mathrm{liq}\right)\to CO\left(\mathrm{g}\right)+3\ H_2\left(\mathrm{g}\right)\)
(g) \(CH_4\left(\mathrm{g}\right)+H_2O\left(\mathrm{liq}\right)+
Callstack:
at (Bookshelves/Physical_and_Theoretical_Chemistry_Textbook_Maps/Thermodynamics_and_Chemical_Equilibrium_(Ellgen)/08:_Enthalpy_and_Thermochemical_Cycles/8.10:_Problems), /content/body/p[25]/span, line 1, column 1
(h) \(C_2H_4\left(\mathrm{g}\right)+CO\left(\mathrm{g}\right)+\ H_2\left(\mathrm{g}\right)\to CH_3CH_2CHO\left(\mathrm{liq}\right)\)
Notes
\(^{1}\) Data compiled by The Committee on Data for Science and Technology (CODATA) and reprinted in D. R. Linde, Editor, The Handbook of Chemistry and Physics, 79\({}^{th}\) Edition (1998-1999), CRC Press, Section 5.
\({}^{2}\) D. R. Linde, op. cit., p. 6-104.


